В статье рассматриваются возможности использования профессионально ориентированных математических задач с экономическим содержанием в реализации профессиональной направленности обучения математике как необходимой составляющей профессиональной компетентности будущих специалистов финансовой сферы.
Ключевые слова: профессионально ориентированные задачи, профессиональная направленность обучения математике, профессиональная компетентность, математическая модель, математическое моделирование экономических процессов.
Необходимой составляющей профессиональной деятельности современного специалиста финансовой сферы является использование математического аппарата для решения различных экономических задач. Исследование таких задач требует применения математического моделирования экономических объектов, явлений и процессов, использования количественных методов обработки данных, различных вычислительных средств. Это определяет особую роль математической подготовки будущего экономиста в системе подготовки в высшей школе. В связи с этим организация обучения математике студентов-экономистов требует ориентации на использование профессионально направленных подходов и технологий обучения, позволяющих проектировать образовательный процесс как максимально приближенный к предстоящей профессиональной деятельности.
Профессиональная направленность обучения математике предполагает такое содержание учебного материала и такую организацию его усвоения, которые не нарушают системной логики построения курса математики и позволяют моделировать познавательные и практические задачи профессиональной деятельности экономиста.
Реализация профессионально направленного обучения математике студентов экономических вузов связана с решением трех основных проблем [1]:
- определение его целей и содержания,
- отбор средств организации усвоения содержания,
- повышение мотивации изучения математики.
Определение целей и содержания математической подготовки будущего экономиста в условиях профессионально направленного обучения, то есть решение первой проблемы, должно происходить с учетом целей и содержания его профессиональной деятельности. При условии сохранения логической целостности изучаемой математической дисциплины содержание необходимо обогащать профессионально ориентированным материалом, т. е. материалом, касающимся объектов будущей профессиональной деятельности экономиста (производственных процессов, функционирующих рынков, хозяйствующих агентов, финансовых и информационных потоков). Интегративный характер математики позволяет соединить математическую и профессиональную подготовку будущего экономиста посредством включения такого материала.
Решению второй задачи, связанной с поиском методов и приемов реализации профессиональной направленности обучения математике, будет способствовать использование средств, позволяющих моделировать элементы профессиональной деятельности экономиста. Важнейшим из них, на наш взгляд, является метод математического моделирования реальных экономических процессов и явлений. Математическое образование будущего экономиста призвано обучать умению строить модели, математические по форме, экономические по содержанию. Использование метода математического моделирования способствует развитию интеллектуальных умений, личностных свойств, обеспечивающих выполнение основных видов деятельности в профессиональной сфере.
Поскольку для студентов экономических направлений подготовки математика не является профилирующей дисциплиной, то многие студенты изучают математические дисциплины формально, воспринимают их как абстрактные, знание которых не понадобится ни при последующем изучении специальных дисциплин, ни в будущей профессиональной деятельности. Применение метода математического моделирования позволяет раскрыть экономический смысл математических понятий, показать универсальность математического аппарата для познания действительности, а также демонстрирует прикладную направленность математики. А это способствует осознанию студентами необходимости математических знаний для дальнейшего обучения и профессиональной деятельности, то есть повышает мотивацию изучения математики и позволяет решить третью проблему.
Решение обозначенных проблем, а следовательно, реализация профессиональной направленности обучения математике студентов-экономистов в рамках традиционного обучения в вузе обеспечиваются, по нашему мнению, за счет использования текстовых математических задач с экономическим содержанием, поскольку специфика математики такова, что основным видом учебной деятельности студентов на занятиях по математике является решение задач. Кроме того, такие задачи являются инструментом реализации метода математического моделирования — важнейшего метода обучения и познания действительности средствами математики. В педагогической и методической литературе их называют по-разному: профессионально ориентированные, профессионально направленные, профильные, прикладные, экономико-математические задачи и др. Мы будем называть их профессионально ориентированными математическими задачами. Различные авторы по-разному трактуют понятие такой задачи. Приведем некоторые из них.
- Прикладная задача — это задача, поставленная вне математики и решаемая с помощью математического аппарата.
- Экономико-математическая задача — это задача экономического содержания, для решения которой необходимо использовать математические средства и методы, а также соответствующие умения ими оперировать.
- Профессионально ориентированная задача — это задача, условие и требование которой представляют собой модель некоторой ситуации, возникающей в профессиональной деятельности, а исследование этой ситуации осуществляется средствами математики.
Мы будем понимать под профессионально ориентированной математической задачей такую задачу, содержание которой связано с объектами и процессами будущей профессиональной деятельности обучаемого, а ее исследование с помощью математического аппарата способствует осознанному применению математических знаний при изучении цикла общепрофессиональных и специальных дисциплин, а также формированию профессиональной компетентности будущего специалиста. В профессионально ориентированных математических задачах с экономическим содержанием отражаются межпредметные связи с экономикой и раскрываются прикладные аспекты научных знаний в профессиональной деятельности экономиста.
В профессионально ориентированном обучении математике студентов-экономистов можно выделить следующие направления их подготовки:
- общеобразовательное направление, основная цель которого — базовая математическая подготовка в контексте будущей профессиональной деятельности экономиста.
- развивающее направление, приоритетом которого является развитие качеств мышления и качеств личности.
- прикладное направление, основная его цель — практико-ориентированная подготовка в рамках предполагаемой профессиональной деятельности.
Специфика и особенности профессионально ориентированных математических задач позволяют использовать их в качестве важнейшего средства формирования общекультурных и профессиональных компетенций в рамках всех выделенных направлений.
Рассмотрение профессионально ориентированной математической задачи как многоаспектного явления в профессионально направленном обучении математике будущих экономистов позволило нам определить роль и функции задач в этом процессе [1].
1) Профессионально ориентированная задача может выступать как форма подачи профессионально направленного содержания, т. е. как носитель новых профессионально значимых знаний и способов действий.
2) Такие задачи есть средство реализации метода математического моделирования экономических объектов и процессов, являющегося одним из важнейших методов обучения математике.
3) Использование профессионально ориентированных математических задач позволяет формировать приемы формализации и интерпретации как основные составляющие умения моделировать.
4) Текстовые задачи, имеющие экономическую фабулу, способствуют повышению мотивации изучения математики студентами-экономистами, являются средством развития познавательного интереса студентов, формирования интеллектуальной гибкости, развития качеств мышления.
Все чаще в профессиональной деятельности многих специалистов, в том числе и специалистов финансовой сферы, встречаются ситуации и задачи, решение которых связано с разработкой и составлением математических моделей.
Если попытаться классифицировать математические модели, используемые в экономике, то можно выделить свыше десяти различных признаков, по которым модели можно разбить на ряд классов. К числу таких признаков можно отнести: особенности моделируемого объекта, цели моделирования, назначение модели, учет фактора неопределенности модели, характер математического объекта и мн.др. С точки зрения обучения студентов моделированию средствами дисциплин математического блока из большого числа классификаций экономико-математических моделей наиболее подходящей, на наш взгляд, является классификация, предложенная в пособии [2]. Авторы выделяют следующие типы моделей:
- макроэкономические (описывают экономику страны как единое целое, связывая между собой укрупненные материальные и финансовые показатели: ВВП, потребление, бюджет, занятость, инфляцию и т. д.) и микроэкономические (описывают взаимодействие структурных и функциональных составляющих экономики, т. е. предприятий, фирм и т. д.);
- теоретические (отображают общие свойства экономики и ее компонентов) и прикладные (обеспечивают возможность оценки параметров функционирования конкретного экономического объекта для формулировки практических рекомендаций);
- оптимизационные (связаны с изучением и разработкой методов решения экстремальных задач, с выбором наилучшего варианта из множества вариантов производства, распределения или потребления), равновесные или балансовые (описывают поведение субъектов хозяйствования в стабильных устойчивых состояниях), имитационные (используется машинная имитация изучаемых систем и процессов) и трендовые (описывают развитие моделируемой системы через длительную тенденцию ее основных показателей);
- статические (описывают состояние экономического объекта в конкретный текущий момент или период времени) и динамические (отражают весь экономический процесс, т. е. переход из исходного состояния в конечное);
- детерминированные (предполагают жесткие функциональные связи между элементами модели) и стохастические (допускают наличие случайных воздействий на исследуемые показатели), и другие.
В ходе изучения дисциплин математического блока студентами бакалавриата по направлению «Экономика» (линейная алгебра, математический анализ, методы оптимальных решений, теория игр, теория вероятностей и математическая статистика) создается возможность познакомить студентов со всеми перечисленными типами моделей и сформировать умения по работе с ними за счет использования соответствующих профессионально ориентированных математических задач.
Рассмотрим возможности профессионально ориентированных математических задач курса теории вероятностей и математической статистики в формировании умений студентов-бакалавров направления «Экономика» исследовать стохастические процессы с использованием в качестве формализованных моделей вероятностных формул и законов.
Приведем несколько примеров таких задач.
1) Из пятнадцати акционерных обществ (АО) четыре являются банкротами. Гражданин приобрёл по одной акции пяти АО. Какова вероятность того, что среди купленных акций две окажутся акциями банкротов?
2) Банк решил вложить поровну средств в три предприятия при условии возврата ему каждым предприятием через определенный срок 154 % от вложенной суммы. Вероятность банкротства каждого из предприятий 0,21. Найдите вероятность того, что по истечении срока кредитования банк получит, по крайней мере, вложенную сумму.
3) В большой рекламной фирме 21 % работников получает высокую зарплату. Известно, что 40 % работников фирмы — женщины, а 6,4 % работников — женщины, получающие высокую зарплату. Можно ли утверждать, что на фирме существует дискриминация женщин в оплате труда?
4) Банк разместил свои кредитные ресурсы следующим образом: 25 % — кредиты государственным органам, 30 % — кредиты другим банкам, 45 % — кредиты физическим лицам. Вероятности невозврата кредита соответственно равны 0,01, 0,02 и 0,03. Руководителю кредитного отдела сообщили, что получена информация о невозврате кредита, но факс плохо пропечатал данные клиента. Найдите вероятность того, что это был другой банк.
5) Вероятность того, что клиент банка не вернет заем в период экономического роста, равна 1/7, а в период экономического кризиса — 1/15. Предположим, что вероятность того, что начнется период экономического роста, равна 0,65. Чему равна вероятность того, что случайно выбранный клиент банка не вернет полученный кредит?
6) Каждый день акции корпорации «АБВ» поднимаются в цене или падают в цене на один пункт с вероятностями соответственно 0,75 и 0,25. Найдите вероятность того, что акции после шести дней вернутся к своей первоначальной цене. Принять условие, что изменения цены акции вверх и вниз — независимые события.
7) Вероятность повышения цены акции за один рабочий день на 2 % равна 0,3, вероятность повышения на 0,1 % равна 0,5, а вероятность понижения на 3 % равна 0,2. Найдите математическое ожидание изменения цены акции за 100 рабочих дней, считая, что начальная цена акции составляет 1000 рублей, а относительные изменения цены за различные рабочие дни — независимые случайные величины.
На примере решения задачи 6 рассмотрим возможность формализации стохастического процесса с использованием схемы повторных независимых испытаний.
Решение: Чтобы акции за 6 дней вернулись к первоначальной цене, нужно, чтобы за это время они 3 раза поднялись в цене и 3 раза опустились в цене. Если ввести событие А — «цена акций за 1 день поднялась на один пункт», то по условию задачи его вероятность Р(А)=0,75, а вероятность противоположного события, т. е. того, что цена за 1 день снизится на 1 пункт, соответственно равна 0,25. Поскольку увеличение или снижение цены акций за один день не зависит от того, что произошло с ценой в другие дни, и возможны только два исхода — цена поднялась (успех) или снизилась (неудача), вероятности которых не меняются, то мы имеем дело с независимыми испытаниями Бернулли. Поэтому для решения задачи необходимо воспользоваться формулой Бернулли: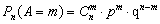 
. При этом достаточно вычислить вероятность того, что из 6 дней 3 дня цена поднималась (или снижалась), т. е. вероятность того, что в шести испытаниях Бернулли событие А наступило ровно 3 раза равна: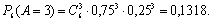 
Рассмотренная задача демонстрирует возможность применения формулы Бернулли в качестве математической модели стохастического типа для исследования экономического процесса изменения цен на акции.
Еще один пример использования профессионально направленных задач в курсе теории вероятностей и математической статистики приведен в статье [3].
Знакомство с различными типами экономико-математических моделей в процессе работы с профессионально ориентированными задачами позволяет сформировать у студентов убеждение о значимости математики в их будущей профессиональной деятельности. Профессионально ориентированные задачи с экономическим содержанием, которые могут быть решены средствами дисциплин математического цикла, в частности теории вероятностей и математической статистики, многообразны и разносторонни. Их использование способствует организации профессионально направленного обучения математике студентов-экономистов, что обеспечивает более успешное изучение специальных дисциплин и формирование профессиональной компетентности будущих экономистов.
Литература:
1. Никаноркина, Н. В. К вопросу о роли профессионально ориентированных задач в формировании профессиональной компетентности студентов экономических вузов при обучении математике [Электронный ресурс] / Н. В. Никаноркина // Письма в Эмиссия. Оффлайн (The Emissia. Offline Letters): электронный научный журнал. — Октябрь 2013, ART 2078. — CПб., 2013 г. Режим доступа: http://www.emissia.org/offline/2013/2078.htm. — [дата обращения 04.08.2014].
2. Замков, О. О. Математические методы в экономике [Текст]: учебник / О. О. Замков, А. В. Толстопятенко. — М.: МГУ им.М. В. Ломоносова, Изд-во Дис, 1998. — 368 с.
3. Зайчикова, И.В., Никаноркина, Н. В. К вопросу о подготовке студентов экономических вузов к использованию математического моделирования в профессиональной деятельности [Текст] / И. В. Зайчикова, Н. В. Никаноркина // Математическое моделирование в экономике, управлении, образовании. Материалы Международной научно-практической конференции. — Калуга: Изд-во «Эйдос», 2012. С.236–241.
