Рассмотрены два метода нахождения корней полинома, получаемого при выполнении алгоритма редукции ранга для пеленгования источников радиоизлучения UCA‑Root‑Rare. Продемонстрированы результаты численного моделирования. Приведён соответствующий листинг программ в пакете Mathcad.
Ключевые слова: UCA‑Root‑Rare, полином, Mathcad, polyroots, roots.
Введение. Определённый подкласс быстрых корреляционных алгоритмов оценивания координат источников излучения (ИИ), требует для своего применения выполнения поиска корней полиномов, степень, а соответственно и число корней, которых, в некоторых случаях, может быть более 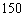 . В таких случаях, некоторые встроенные корни функции Mathcad не позволяют выполнить поиск решений.
. В таких случаях, некоторые встроенные корни функции Mathcad не позволяют выполнить поиск решений.
Цель работы — используя свойства полинома, получаемого при выполнении алгоритма UCA‑Root‑Rare (Rare‑полином) [1], найти решения Rare‑полинома при помощи встроенных функций пакета Mathcad для произвольной степени полинома.
1.Алгоритм UCA‑Root‑Rare. Вычисление координат ИИ, в данном случае азимута, при помощи алгоритма UCA‑Root‑Rare, выполняется путём нахождения корней следующего полиномиального уравнения:
 , (1)
, (1)
где 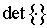 — определитель матрицы,
— определитель матрицы,
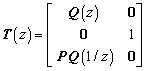 (2)
(2)
матрица размера  ,
,
 (3)
(3)
диагональная матрица размера 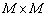 ,
,  оператор диагонализации элементов,
оператор диагонализации элементов,
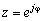 . (4)
. (4)
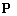 — это
— это  матрица отражений или антидиагональная единичная матрица:
матрица отражений или антидиагональная единичная матрица:
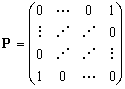 . (5)
. (5)
Используя (1)‑(3) и (5) матрица 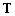 для
для  будет иметь следующий вид:
будет иметь следующий вид:
 . (6)
. (6)
Матрица 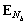 — это матрица собственных векторов, соответствующих подпространству шума корреляционной матрицы данных в пространстве лучей [2].
— это матрица собственных векторов, соответствующих подпространству шума корреляционной матрицы данных в пространстве лучей [2].
Исследование уравнения (1) показывает, что степень полинома будет  , а следовательно уже для
, а следовательно уже для 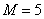 число корней Rare‑полинома будет равным
число корней Rare‑полинома будет равным 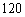 .
.
2. Встроенные функции пакета Mathcad. Встроенные функции Mathcad в состоянии решить любое алгебраическое уравнение. Для решения уравнения с одним неизвестным можно использовать функции root и polyroots. Mathcad решает уравнения итерационным методом, поэтому перед решением необходимо задать начальное приближение для всех корней [3].
2.А. Функция root.
Функция root используется для решения одного уравнения с одним неизвестным. Обращение к функции: root(f(x)), где 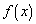 — выражение, равное нулю;
— выражение, равное нулю; 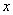 — аргумент, варьируя который, система ищет значение, обращающее функцию в нуль. Функция
— аргумент, варьируя который, система ищет значение, обращающее функцию в нуль. Функция  и аргумент
и аргумент 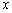 должны быть скалярами, то есть результат вычисления функции — число, а не вектор или матрица. Функция root использует итерационный метод секущих. Корень уравнения — ближайшее к начальному приближению значение
должны быть скалярами, то есть результат вычисления функции — число, а не вектор или матрица. Функция root использует итерационный метод секущих. Корень уравнения — ближайшее к начальному приближению значение 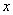 , обращающее функцию
, обращающее функцию  в нуль. Если корней несколько, для отыскания каждого корня необходимо задавать свое начальное приближение. Если уравнение не имеет действительных корней, то есть функция
в нуль. Если корней несколько, для отыскания каждого корня необходимо задавать свое начальное приближение. Если уравнение не имеет действительных корней, то есть функция  нигде не равна нулю, то Mathcad выводит комплексное число [3].
нигде не равна нулю, то Mathcad выводит комплексное число [3].
2.А. Функция polyroots
Для нахождения корней полинома можно использовать функцию polyroots(K), которая определяет все корни полинома одновременно. Здесь 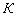 — вектор коэффициентов полинома, начиная со свободного члена. Нулевые коэффициенты опускать нельзя. Если полином имеет
— вектор коэффициентов полинома, начиная со свободного члена. Нулевые коэффициенты опускать нельзя. Если полином имеет  корней (с учетом кратности), то вектор
корней (с учетом кратности), то вектор 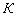 включает в себя
включает в себя 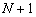 коэффициент. Начальное приближение вводить не надо. Следует обратить внимание, что вектор
коэффициент. Начальное приближение вводить не надо. Следует обратить внимание, что вектор 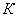 должен содержать от
должен содержать от 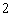 до
до 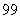 коэффициентов.
коэффициентов.
3. Получение оценок. Вэтом разделе рассматриваются оценки, получаемые при решении уравнения (1) при помощи функций polyroots и root.
3.А. Получение решений при помощи функции polyroots.
Как говорилось ранее, функция polyroots работает только с полиномами, степень которых не превышает 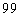 . Накладываемое функцией polyroots ограничение позволяет применять её для решения уравнения (1) в случае, если параметр размера
. Накладываемое функцией polyroots ограничение позволяет применять её для решения уравнения (1) в случае, если параметр размера 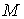 матрицы
матрицы 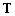 не превышает
не превышает 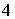 , что будет соответствовать
, что будет соответствовать 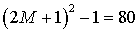 корням. Для
корням. Для  применение функции polyroots невозможно, поскольку в этом случае степень Rare‑полинома превышает значение
применение функции polyroots невозможно, поскольку в этом случае степень Rare‑полинома превышает значение 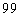 и будет больше
и будет больше 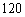 . Решения уравнения (1) при помощи функции polyroots показаны на рисунке 1 а), где крестиком обозначены истинные координаты азимута трех источников, кружками обозначены корни уравнения (1), пунктирной линией показана единичная окружность.
. Решения уравнения (1) при помощи функции polyroots показаны на рисунке 1 а), где крестиком обозначены истинные координаты азимута трех источников, кружками обозначены корни уравнения (1), пунктирной линией показана единичная окружность.

а) б)
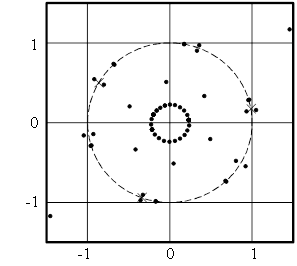
Рис. 1. Решения Rare‑полинома при помощи функции: а) polyroots, 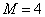 ; б) root,
; б) root,  . Азимут источников излучения
. Азимут источников излучения 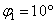 ,
, 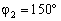 ,
, 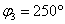 .
.
3.А. Получение решений при помощи функции root.
Исследование уравнения (1) показывает, что истинными оценками азимута будут являться только те корни, которые максимально близко расположены к единичной окружности. Следовательно, для поиска корней полинома степени большей, чем  можно применить функцию root, ограничив область поиска значениями, лежащими на единичной окружности взяв их с некоторым шагом. Для комплексной плоскости этим значениям будет соответствовать некоторый угол
можно применить функцию root, ограничив область поиска значениями, лежащими на единичной окружности взяв их с некоторым шагом. Для комплексной плоскости этим значениям будет соответствовать некоторый угол 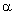 , косинус которого будет соответствовать действительной части числа, а синус мнимой. Ниже приведён листинг программы в пакете Mathcad реализующий поиск корней Rare‑полинома произвольной степени при помощи функции root.
, косинус которого будет соответствовать действительной части числа, а синус мнимой. Ниже приведён листинг программы в пакете Mathcad реализующий поиск корней Rare‑полинома произвольной степени при помощи функции root.
Листинг 1. Нахождение корней Rare‑полинома произвольной степени
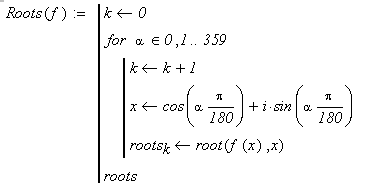
где  — это соответствующий полном уравнения (1). В случае, если заданы только коэффициенты полинома, то необходимо преобразовать функцию
— это соответствующий полном уравнения (1). В случае, если заданы только коэффициенты полинома, то необходимо преобразовать функцию 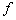 в выражение, используя, например, следующий листинг:
в выражение, используя, например, следующий листинг:
Листинг 2. Преобразование коэффициентов полинома в выражение
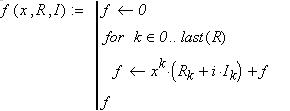
где 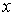 — это переменная полинома,
— это переменная полинома, 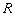 — вектор столбец из действительных частей коэффициентов полинома,
— вектор столбец из действительных частей коэффициентов полинома, 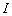 — вектор столбец из мнимых частей полинома. После применения листинга 2 необходимо выполнить листинг 1. Соответствующее решение уравнения (1) показаны на рисунке 1 б).
— вектор столбец из мнимых частей полинома. После применения листинга 2 необходимо выполнить листинг 1. Соответствующее решение уравнения (1) показаны на рисунке 1 б).
Одним из свойств корней Rare‑полинома, является то, что все его корни обладают так называемым свойством взаимной сопряжённости, которое означает, что если 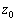 — это корень полинома, то
— это корень полинома, то 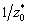 также будет корнем полинома [4]. Иными словами, корни симметричны относительно единичной окружности, что можно наблюдать на рисунке 1 а). Для корней вблизи центра окружности, их
также будет корнем полинома [4]. Иными словами, корни симметричны относительно единичной окружности, что можно наблюдать на рисунке 1 а). Для корней вблизи центра окружности, их 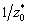 парные корни находятся за пределами области построения графика, и охватывают окружность с наружи таким же плотным кольцом, как и корни вблизи центра окружности.
парные корни находятся за пределами области построения графика, и охватывают окружность с наружи таким же плотным кольцом, как и корни вблизи центра окружности.
Поиск корней по методу, приведённому в листингах 1 и 2, даёт только один корень. Учитывать корень 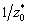 нет необходимости, однако при желании это возможно сделать, просто выполнив операцию
нет необходимости, однако при желании это возможно сделать, просто выполнив операцию 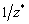 для каждого найденного решения.
для каждого найденного решения.
Следует также обратить внимание, на то, что полученные решения по листингам 1 и 2 получаются несколько искажёнными, а кольцо вблизи центра окружности на рисунке 1 б) имеет деформацию, в отличие от аналогичного кольца на рисунке 1 а). Такое различие может быть вызвано как большой дискретностью шага поиска, так и отличием методов поиска решений функций polyroots иroot.
Заключение. В статье были рассмотрены два варианта нахождения корней полинома, получаемого в результате нахождения определителя в уравнении (1). Приведён соответствующий листинг предлагаемых методов. На численном примере в графическом отображении показаны отличия, между нахождением корней полинома стандартными функциями пакета Mathcad polyroots иroot.
Литература:
1. Pesavento M., Böhme J. F. Direction of arrival estimation in uniform circular arrays composed of directional elements // Sensor Array and Multichannel Signal Processing Workshop. 2002. No 8. P. 503–507.
2. Marple L. Digital spectral analysis with applications. New Jersey: Prentice-Hall, 1987. P. 492.
3. Макаров Е. Инженерные расчёты в Mathcad 15: Учебный курс — Спб.: Питер, 2011. — 400 с.: ил.
4. Li. H. Y., Xie J. L., He Z. S. A fast DOA estimation algorithm for uniform circular arrays in the presence of unknown mutual coupling // Progress In Electromagnetics Research C, 2011, Vol. 21, 257–271.







