Рассматриваются методы спектрального сверхразрешения, основанные на модификации собственных значений корреляционной матрицы принимаемого сигнала. Последующий учёт априорной информации используется для получения улучшенного частотного разрешения.
Ключевые слова: спектр, корреляция, модификация собственных значений.
Введение. Применение параметрических моделей случайных процессов обусловлено возможностью получения на основе этих моделей более точных оценок спектральной плотности мощности (СПМ), чем это возможно с помощью классических методов спектрального оценивания [1]. Классические методы дают оценки СПМ по взвешенной последовательности данных или оценок автокорреляции. Отсутствующие данные или неоценённые значения автокорреляционной последовательности за пределами применяемого окна неявно полагаются равными нулю, что является нереалистическим допущением и, как следствие, приводит к искажениям спектральных оценок. На практике часто имеется некоторая априорная информация относительно процесса, из которого берутся отсчёты данных, что позволяет принимать более адекватные допущения об обрабатываемых данных.
Так, при короткой выборке x процесса параметрические методы оценки СПМ дают лучшее спектральное разрешение и оценивание частоты, однако при низких отношениях сигнал-шум параметрические методы (например, авторегрессионный метод и метод Прони) не в состоянии разрешить близкие по частоте моды [1].
Цель статьи — используя априорную информацию о сигнале, разработать метод улучшенного спектрального разрешения, основанного на анализе априорной информации.
Одним из методов улучшения характеристик спектрального оценивания является анализ собственных значений λn оценок R автокорреляционной матрицы Rx анализируемого процесса, полученных по зашумлённой выборке x. Ключевой операцией в этих методах является разделение информации, содержащейся в R, на два векторных подпространства — подпространство сигнала и подпространство шума [1].
Сравним различные методы оценки СПМ на примере анализа процесса, многомодового по спектру процесса с нормированной корреляционной матрицей Rx= [Rj,k], соответствующей аддитивной сумме M односвязных марковских процессов:
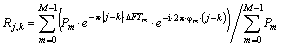 ,
,
где ΔFTm — относительная ширина m‑ой спектральной моды, φm — относительная частота m‑ой моды, Pm — относительная мощность моды, M — количество спектральных мод, i — мнимая единица.
В качестве контрольной модели используем авторегрессионную модель (АР) 200-го порядка, коэффициенты которой рассчитываются по нормальному уравнению Юла-Уолкера [1]:
ax=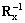 i,
i,
где ax — вектор коэффициентов авторегрессии контрольной АР‑модели, i — крайний левый столбец единичной матрицы. Она является идеализированной и не содержит мешающие компоненты, в качестве которых используется аддитивный комплексный белый гауссовский шум с нулевым средним и дисперсией 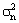 .
.
Критерий сравнения. Для сравнения используются два метода, основанные на анализе собственных чисел λn (p+1)×(p+1)‑мерной матицы R для её последующей модификации R͂ с целью получения вектора a=R͂−1i оценок коэффициентов авторегрессии оптимизированной АР-модели p‑го порядка.
В качестве критерия эффективности спектрального анализа используется нормированный к числу L спектральных отсчётов квадрат среднего отклонения ε между нормированными СПМ c= [сl] контрольной модели и s= [sl] оптимизированной модели, полученной по зашумлённым данным:
ε=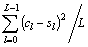 =(с − s)T(с − s)/L, (1)
=(с − s)T(с − s)/L, (1)
где T — знак транспонирования.
Моделирование зашумлённой выборки x осуществляется путём суммирования полученной при помощи контрольной АР-модели выборки x идеализированного процесса с отсчётами комплексного белого гауссовского шума.
Первый метод основан на получении матрицы R͂1 из оценки автокорреляционной матицы R путём вычитания из её главной диагонали оценки мощности шума, в качестве которой принимается минимальное собственное число λmin≈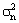 матрицы R [2]:
матрицы R [2]:
R͂1=R−λminI,
где λmin=min(λ) — минимальное собственное число матрицы R, соответствующее оценке мощности шумовой компоненты аддитивной смеси x сигнала и шума, I — единичная матрица, λ — вектор собственных чисел матрицы R. Тогда вектор АР-коэффициентов a1 для первой модели: a1=(R͂1)−1i.
Второй метод основан на введении в сигнал априорной информации, содержащей значение максимального собственного числа λx матрицы Rx. Зная λx и максимальное собственное значение λmax=max(λ) матрицы R можно найти коэффициент k, характеризующий изменение собственных чисел корреляционной матрицы Rx сигнала, вызванное его зашумлением при передаче по каналу связи, исходя из равенства: (λmax)k=λx. Тогда модифицированный вектор λ̃= [λ̃0, λ̃1, …, λ̃ p] собственных значений может быть рассчитан следующим образом: λ̃ = [(λ̃0)k, (λ̃1)k, …, (λ̃p)k], где k=ln(λx)/ln(λmax).
Восстанавливая модифицированную корреляционную матрицу R͂2 через преобразование Карунена-Лоева, получаем:
R͂2=G [diag(λ̃)] G−1
где G — собственный вектор матрицы R. Вектор АР-коэффициентов для второй модели обозначим как a2=(R͂2)−1i.
С целью оценки эффективности первого и предлагаемого второго методов проведём статистическое моделирование, основанное на спектральном анализе зашумлённой выборки x, описание которой приведено выше. При этом параметры модели следующие: M=3, ΔFT0 = ΔFT1 = ΔFT2 = 0.1, φ0 = 0.25, φ1 = 0.1, φ2 = 0.2, P0 = 1, P1 = P2 = 0.2. Модель имитирует сигнал 3U0 напряжения, возникающего в устройстве релейной защиты высоковольтных (6…10 кВ) кабельных сетях при однофазном замыкании на землю [3] и содержит три низкочастотных гармоники переменного тока частотой 50 Гц.
Проведённое моделирование выбранных методов показывает, что при малых (−10...−15 дБ) отношениях b сигнал-шум наилучшим, с точки зрения выбранного критерия (1), является предлагаемый второй метод, основанный на учёте априорной информации о максимальном собственном значении λx. Первый метод даёт выигрыши при значительном превышении уровня полезного сигнала над шумом (b>5 дБ). Отсутствие модификации корреляционной матрицы при синтезе АР-моделей целесообразно в рассмотренной задаче при b>10 дБ.
Таблица
СКО предлагаемых методов
|
b, дБ |
−15 |
−10 |
−5 |
0 |
|
ε1 |
0,05 |
2,162∙10–3 |
1,234∙10–3 |
8,607∙10–4 |
|
ε2 |
5,013∙10–3 |
1,361∙10–3 |
8,931∙10–4 |
5,744∙10–4 |
|
ε3 |
0,45 |
0,138 |
0,032 |
1,65∙10–3 |
Анализ таблицы показывает, что при b=−5 дБ отношение μ=ε1/ε2 СКО отклонений спектров ε1 и ε2 для первого и второго методов соответственно составляет μ=1.38, а при b=−15 дБ достигает величины μ=9.97.
Заключение. Использование априорной информации о максимальном собственном числе λx нормированной корреляционной матрицы Rx передаваемого сигнала позволяет сократить в 9.97 раз отклонения ε спектров контрольной и рабочей моделей, построенных по модифицированной по второму методу корреляционной матрице R͂2 по сравнению с известным первым методом, использующим величину R͂1. Выигрыш достигается за счёт учёта дополнительной информации о спектре λ собственных значений сигнала для синтеза модифицированной матрицы R͂2 путём использования преобразования Карунена — Лоева.
Литература:
1. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения: Пер. с англ.— М.: Мир, 1990.— 584 с.
2. Кошелев В. И., Андреев В. Г. Оценка собственных значений в задаче обработки эхо-сигналов // 100-летие начала использования электромагнитных волн для передачи сообщений и зарождения радиотехники: тезисы докладов Международной конференции, г. Москва, 4 6 мая 1995 г.— М.: Изд-во журнала «Радиотехника», 1995.— C. 180‑181.
3. Андреев В. А. Релейная защита и автоматика систем электроснабжения.— М.: Высшая школа, 1991.— 496 с.







