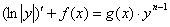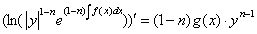В статье представлены усовершенствованные варианты логарифмических методов решения некоторых видов дифференциальных уравнений.
Здесь и далее: 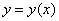 ,
, 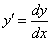 ,
,
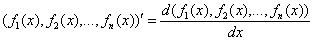 ,
,
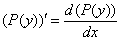 ,
, 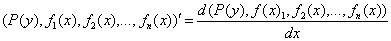 ,
,
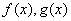 — известные интегрируемые функции,
— известные интегрируемые функции, 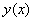 — неизвестная функция,
— неизвестная функция, 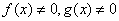 ,
,
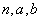 – вещественные постоянные,
– вещественные постоянные, 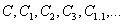 – константы интегрирования.
– константы интегрирования.
1. Интегрирование улучшенным вариантом логарифмического метода уравнений вида:
Улучшенный метод решения:
Полагая 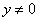 , и разделяя уравнение (1) на
, и разделяя уравнение (1) на 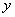 :
:
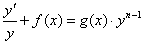
Далее действия очевидны:
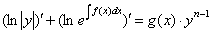
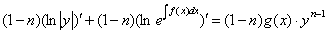
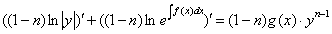
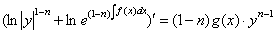
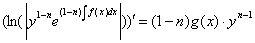
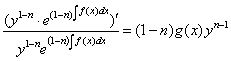
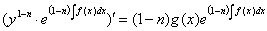
Интегрируя:
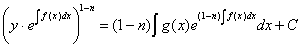
Окончательно:
Вторым решением будет, очевидно:
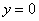
1.1. Если 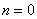 , то уравнение (1) будет иметь вид
, то уравнение (1) будет иметь вид
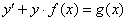 (2)
(2)
Метод интегрирования: так как, по предположению, 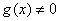 , то и
, то и 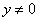 , и уравнение (2) может быть представлено в виде
, и уравнение (2) может быть представлено в виде
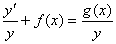
Далее действия сходные с предыдущими:
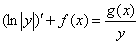
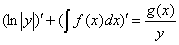
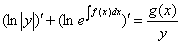
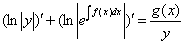
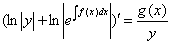
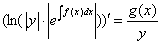 , что равносильно
, что равносильно 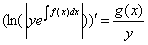 , далее
, далее
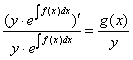
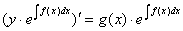
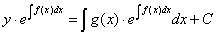
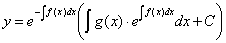 (3)
(3)
В данном случае метод был показан только для целых чисел 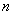 в уравнении (1), за исключением
в уравнении (1), за исключением 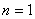 . Действия, подобные указанным, очевидно, применимы и к случаю, когда
. Действия, подобные указанным, очевидно, применимы и к случаю, когда 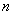 — любое вещественное число, не равное единице, если после шага (1.1) сразу дифференцировать первое слагаемое по правилу дифференцирования логарифма. Но это затем приведет к долгим и не интересным выкладкам. В 4-м пункте статьи будет показан менее громоздкий вариант метода, который устраняет лишние действия.
— любое вещественное число, не равное единице, если после шага (1.1) сразу дифференцировать первое слагаемое по правилу дифференцирования логарифма. Но это затем приведет к долгим и не интересным выкладкам. В 4-м пункте статьи будет показан менее громоздкий вариант метода, который устраняет лишние действия.
2. Улучшенный метод интегрирования уравнения вида:
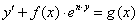
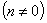
Ход метода:
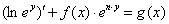
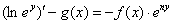
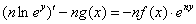
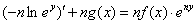
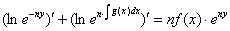
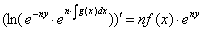
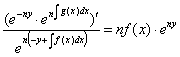
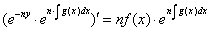
Интегрируя: 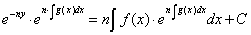
Окончательно: 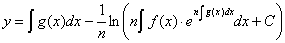
3. Уравнения вида:
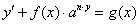
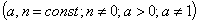
Метод интегрирования: в этом случае допустимо подставить 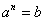 , тогда уравнение будет иметь вид:
, тогда уравнение будет иметь вид:
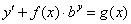
Далее действия очевидны:
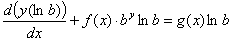
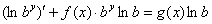
Подстановка 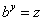 приводит последнее уравнение к уравнению вида (1) [при
приводит последнее уравнение к уравнению вида (1) [при 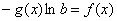 ,
, 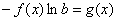 ,
, 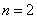 ], и его решение по соответствующей формуле будет:
], и его решение по соответствующей формуле будет:
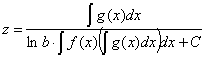 ,
,
возвращаясь к подстановке:
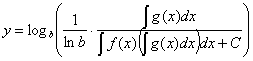 , где
, где 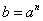
4. Частные случаи хода логарифмического метода:
4.1. Решая аналогично уравнение (2), придем (при 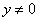 ) к уравнению
) к уравнению 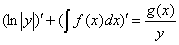
Оно будет равносильно уравнению: 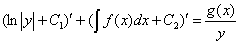
Его можно представить в виде:
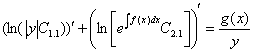
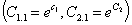
В свою очередь, 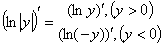 ,
,
Тогда, если 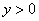 , то
, то 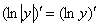 .
.
Если 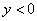 , то
, то 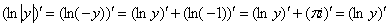 ,
,
так как 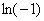 — однозначная комплексная постоянная, а значит допустимо дифференцирование по комплексной функции, а дифференциал от комплексной постоянной равен нулю. Исходя из этого, во всех вариантах логарифмического метода решения дифференциальных уравнений, выражение
— однозначная комплексная постоянная, а значит допустимо дифференцирование по комплексной функции, а дифференциал от комплексной постоянной равен нулю. Исходя из этого, во всех вариантах логарифмического метода решения дифференциальных уравнений, выражение 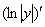 может быть в данных случаях всегда заменено выражением
может быть в данных случаях всегда заменено выражением 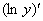 , и наоборот. На результат это не повлияет. Аналогично обстоит дело и с
, и наоборот. На результат это не повлияет. Аналогично обстоит дело и с 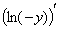 , которое при дифференцировании, так же как и
, которое при дифференцировании, так же как и 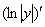 , тоже обращается в
, тоже обращается в 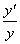 . Исходя из этого, полученное уравнение
. Исходя из этого, полученное уравнение 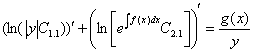 может быть заменено равносильным ему
может быть заменено равносильным ему 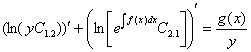 , где
, где 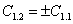 , в зависимости от того, предположено ли
, в зависимости от того, предположено ли 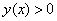 , или
, или 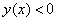 соответственно. Далее, по формуле сложения производных:
соответственно. Далее, по формуле сложения производных: 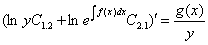 , или
, или
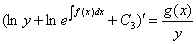 , где
, где 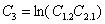
Далее действия очевидны:
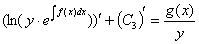 ,
,
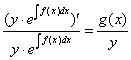
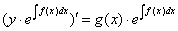
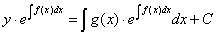
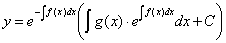
4.2. Так как 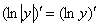 , то первый метод решения уравнений вида
, то первый метод решения уравнений вида 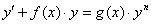 , где
, где 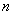 — будет теперь любое вещественное число, удовлетворяющее условию
— будет теперь любое вещественное число, удовлетворяющее условию 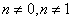 , может быть заменен более облегченным;
, может быть заменен более облегченным;
Полагая 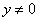 , и разделяя уравнение на
, и разделяя уравнение на 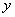 :
:
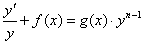
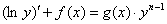
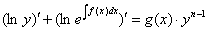
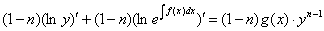
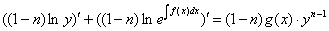
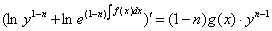
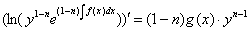
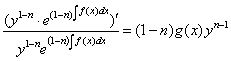
Интегрируя: 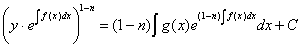
Окончательно: 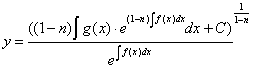
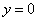
В только что описанном варианте метода уже нет лишних элементарных преобразований, которые нисколько не интересны и лишь увеличивают количество действий.
4.3. Аналогичным пошаговым упрощенным методом для уравнений вида 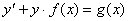
будет (полагая 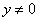 ) следующий:
) следующий:
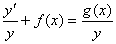
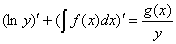
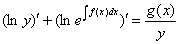
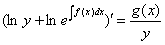
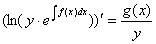
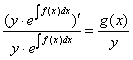
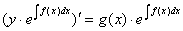
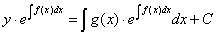
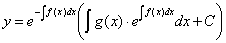
4.4. Уравнение
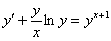 (4)
(4)
тоже может быть решено логарифмическим методом, если избавится от модуля под знаком дифференциала логарифма. Если 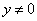 , то исходное уравнение будет равносильно
, то исходное уравнение будет равносильно 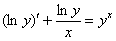 ; затем пошаговыми действиями выводится конечное решение:
; затем пошаговыми действиями выводится конечное решение: 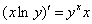 ,
, 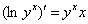 , после чего допустима подстановка
, после чего допустима подстановка 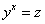 .
.
Окончательное решение: 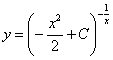 , а также
, а также 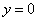 . Подстановка
. Подстановка 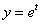 дает то же решение.
дает то же решение.
Общим видом уравнения (4) является:
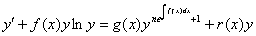
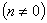 (5)
(5)
Метод решения:
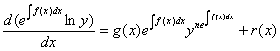
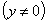
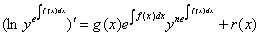
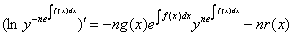
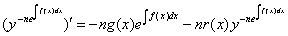
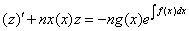 , где
, где 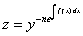 ,
,
а решением последнего уравнения служит формула (3).
Выбор же 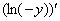 , или
, или 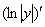 в качестве первого слагаемого в первом шаге решения уравнений (4), или (5), снова приводит ко многим лишним действиям.
в качестве первого слагаемого в первом шаге решения уравнений (4), или (5), снова приводит ко многим лишним действиям.
Литература:
1. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления: в 3 т. Изд-во: Физматгиз, 1959 г.
2. Пономаренко А. Н. Логарифмический метод решения обыкновенных дифференциальных уравнений первого порядка. Журнал «Молодой ученый» (№ 7 (54), июль 2013 г.), с. 3–5.







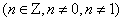 (1)
(1)