В соответствии с образовательным стандартом высшего профессионального образования по направлению подготовки 250400 Технология лесозаготовительных и деревоперерабатывающих производств (квалификация (степень) «бакалавр») при изучении дисциплины «Моделирование и оптимизация процессов», входящей в базовую часть математического и естественно-научного цикла, бакалавр должен:
знать: основные понятия и методы математического анализа, теорию вероятностей и математической статистики, дискретной математики; методы получения математических моделей технологических процессов; математические методы и программы ЭВМ для решения моделей;
уметь: использовать математические методы в технических приложениях; использовать возможности вычислительной техники и программного обеспечения; самостоятельно формулировать задачу научного исследования, наметить пути ее решения, организовать проведение научных исследований, делать выводы и обобщения;
владеть: методами математического анализа; средствами компьютерной графики (ввод, вывод, отображение, преобразование и редактирование графических объектов на ПЭВМ); основными методами работы на ПЭВМ с прикладными программными средствами; математическими методами планирования эксперимента для получения математических моделей описания технологических процессов, методами статистической обработки результатов эксперимента и проверки адекватности математической модели.
Для оптимизации учебного процесса и обеспечения межпредметной взаимосвязи между дисциплинами естественно-научного цикла при организации курса “Моделирование и оптимизация процессов” на кафедре МиММ ПГУАС предлагается проводить занятия по принципу: одна задача — несколько решений [1,2]. Реализацию этого принципа можно показать на примере транспортной задачи.
Пример. На три базы a i поступил однородный груз в количестве: 100; 200; 90 тонн. Полученный груз требуется перевезти в три пункта b j, потребности которых составляют: 190; 120; 30 тонн. Расстояние Cij в ед.км. (i=1,2,3; j=2,2,3) между пунктами отправления и пунктами назначения приведены в табл.1.
Таблица 1
|
b j a I |
b 1=190 |
b 2=120 |
b 3=30 |
|
a 1=100 |
4 |
2 |
3 |
|
a 2=200 |
3 |
5 |
3 |
|
a 3=90 |
1 |
4 |
6 |
Рассмотрим решение транспортной задачи методом потенциалов при изучении дисциплины «Моделирование и оптимизация процессов».
Так как ∑ai=100+200+90=390, ∑bj=190+120+30=340, т. е. ∑ai≠∑bj, имеем открытую модель транспортной задачи, где суммарные запасы превышают суммарные потребности.
Математическая модель задачи формулируется следующим образом:
Найти min значение линейной функции 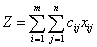 при ограничениях
при ограничениях
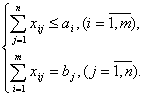
Данная открытая модель решается приведением к закрытой путем введения фиктивного потребителя, потребности которого bn+1=∑aI — ∑bj=390–340=50. Стоимость перевозок для потребителя bn+1 полагается равной нулю.
Составим первоначальный план перевозок, используя метод наименьшей стоимости, таблица 2.
Таблица 2
|
b j a I |
b 1=190 |
b 2=120 |
b 3=30 |
b 4=50 |
|
a 1=100 |
4 |
2 100 |
3 |
0 |
|
a 2=200 |
3 100 |
5 20 |
3 30 |
0 50 |
|
a 3=90 |
1 90 |
4 |
6 |
0 |
Проверяем оптимальность полученного плана перевозок методом потенциалов. Поставщику ставим в соответствие потенциалы Ui, а потребителюVj и определяем их исходя из условия Cij=Ui+Vj. Для всех свободных клеток находим ∆Cij (таблица 3). Так как для свободных клеток все ∆Cij≥0, то получен оптимальный план перевозок.
Таблица 3
|
Vj UI |
v 1=0 |
v 2=2 |
v 3=0 |
v 4=-3 |
|
U 1=0 |
4 0 |
2 100 |
3 0 |
0 –3 |
|
U 2=3 |
3 100 |
5 20 |
3 30 |
0 50 |
|
u 3=1 |
1 90 |
4 3 |
6 1 |
0 –2 |
Таким образом, получили оптимальный план перевозок
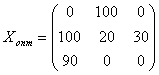 ,
,
обеспечивающий минимальную стоимость перевозок:
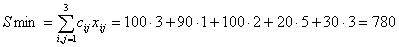 .
.
Теперь рассмотрим реализацию представленной транспортной задачи (таблица 1) при изучении дисциплины «Математические методы и модели в расчетах на ЭВМ». Решение задачи производим в программе Microsoft Excel. Создаем на Листе Excel таблицу с исходными данными и таблицу с изменяемыми ячейками, в которые будут записываться результаты плана перевозок (рис.1).
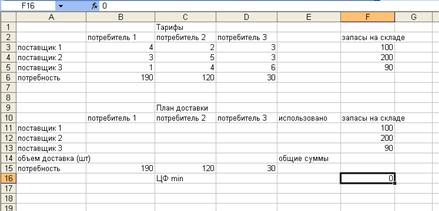
Рис. 1. Фрагмент листа Excel с исходными данными
Для поиска оптимального плана перевозок, соответствующего минимальному значению ЦФ, воспользуемся надстройкой Поиск решения, активизировав параметры: линейная функция и неотрицательные значения. Результат выполнения поиска решения представлен на рисунке 2.
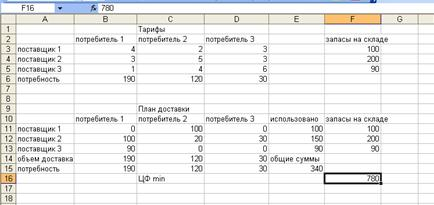
Рис. 2. Результат расчета.
Предложенный метод организации учебного процесса позволяет студентам оценить, выделить преимущества каждого метода решения предлагаемой задачи и выбрать наиболее оптимальный [3,4,5].
Выстроенный таким образом учебный процесс, на наш взгляд, в полной мере соответствует новым образовательным стандартам и способствует формированию профессиональных знаний, умений и навыков.
Литература:
1. Бочкарева, О. В. Математические задачи как средство формирования профессиональных качеств личности / О. В. Бочкарева, Т. Ю. Новичкова, О. В. Снежкина, Р. А. Ладин // Современные проблемы науки и образования.–2014.–№ 2; URL: www.science-education.ru/116–12584
2. Ладин, Р. А. Математика и междисциплинарные связи/Р. А. Ладин, О. В. Снежкина, О. В. Бочкарева, Н. В. Титова//Молодой ученый.- 2014.- № 1.- С. 550–552.
3. Бочкарева, О. В. Формирование профессиональных умений на занятиях по математике/ О. В. Бочкарева, О. В. Снежкина, М. А. Сироткина // Молодой ученый.- 2014.- № 2 (61).- С. 735–738.
4. Ладин, Р. А. Математика в учебном процессе строительного вуза/ Р. А. Ладин, О. В. Снежкина, Г. А. Левова //Вестник магистратуры.- 2013.- № 12–4 (27).- С. 56–59.
5. Сироткина, М. А. К вопросу о профессиональной направленности обучения математике / М. А. Сироткина, О. В. Бочкарева, О. В. Снежкина // Вестник магистратуры.- 2014.- № 2 (29).-С. 59–61.







