Различные модификации метода последовательных приближений для одного уравнения и системы уравнений рассмотрены в работах [1–3].
В данной работе исследуется модифицированная система аналогичная системe рассмотренный в работе [3].
Рассмотрим систему дифференциальных уравнений
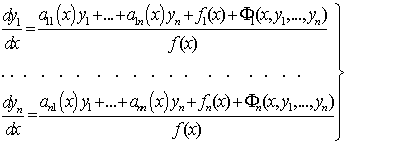 (1)
(1)
где 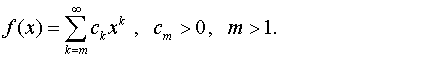
Правые части системы (1) определены, непрерывны, а функции 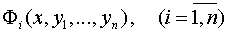 непрерывны и обладают непрерывными частными производными по переменными
непрерывны и обладают непрерывными частными производными по переменными 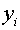 в окрестности
в окрестности
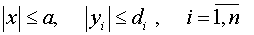 (2)
(2)
начала координат.
Пусть выполнены условия: 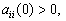
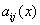 непрерывные функции
непрерывные функции
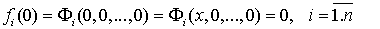 (3)
(3)
Тогда получим:
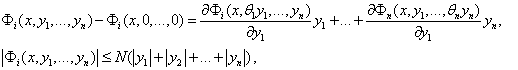 (4)
(4)
здесь 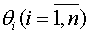 достаточное малое число,
достаточное малое число,
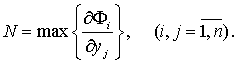
Для дальнейшего исследования введём следующие обозначения:
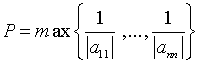
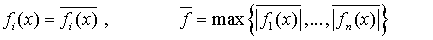
Ищем решение системы, удовлетворяющие начальным условиям
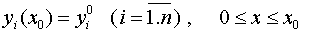 (5)
(5)
причем эти условия подчинены неравенствам
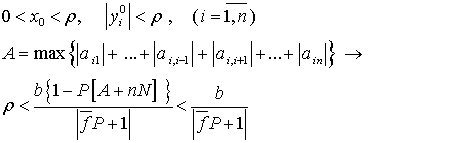
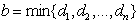
Отметим, что решение находим на сегмента 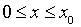 .
.
В дальнейшем у функции 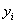 будет два индекса: первый индекс — номер функции, второй индекс — номер последовательных приближений.
будет два индекса: первый индекс — номер функции, второй индекс — номер последовательных приближений.
Приближения выбираем так, что выполняется условие:
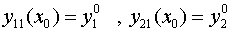 (6)
(6)
Первое приближение отыскиваем как решение системы укороченных дифференциальных уравнений
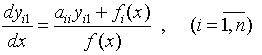 (7)
(7)
Введя функции 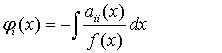
получим общее решение системы (7)
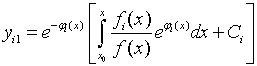 .
.
Вследствие выбора начальных условий по формулам (5) и (6) получим 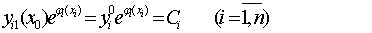
Считаем, что начальные условия выбраны так, что
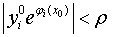
Вторые приближения находим из следующей системы дифференциальных уравнений
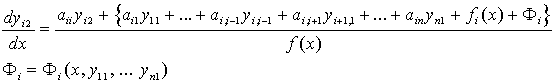
Отсюда получим выражения для второго приближения
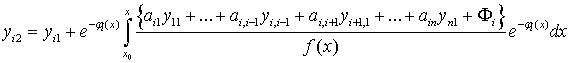
совершенно аналогично получим, что 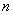 -е приближения находятся из системы
-е приближения находятся из системы
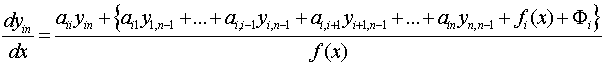 .
.
Отсюда получим
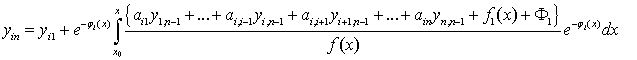 Оценим все последовательные приближения, с целью показать, что они не выходят за пределы области определения правых частей системы (1). Пользуясь формулами (4), (8) и тем, что
Оценим все последовательные приближения, с целью показать, что они не выходят за пределы области определения правых частей системы (1). Пользуясь формулами (4), (8) и тем, что
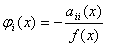
т. е. функции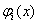 убывают, получим:
убывают, получим:
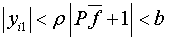 (9)
(9)
Пользуясь выше перечисленными формулами, а также (4), (9) получим 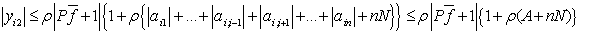
Проводя исследования методом математической индукции, предполагаем, что имеет место оценка
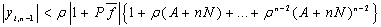
Получим, что имеет место также оценка 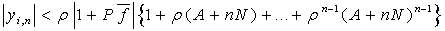
Из полученных оценок следует, что все последовательные приближения не выходят за пределы области (2).
Далее пользуясь методом математической индукции оценим разности 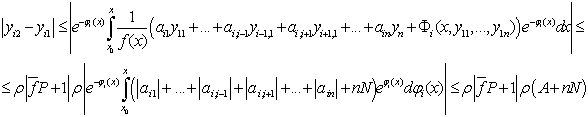
Предполагая, что верна оценка
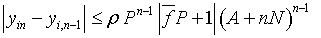
легко докажем, что верна и оценка
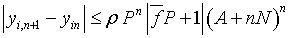
Из полученных оценок для разности ясно, что ряды
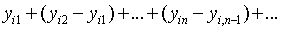
абсолютно и равномерно сходятся и их суммы будут некоторые функции.
Очевидно, что эти функции удовлетворяют некоторой системе интегральных и соответственно, системы дифференциальных уравнений (1) с начальными условиями (5). Затем при наших предположениях доказывается, что
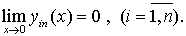
Т. е. доказана следующая теорема:
Теорема. Пусть правые части системы (1) определены, непрерывны, а функции 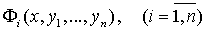 непрерывны и обладают непрерывными частными производными по
непрерывны и обладают непрерывными частными производными по 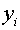 в окрестности (2) начала координат и выполнены условия (3), тогда существует решение системы (1) удовлетворяющее условию (5) которая стремится к нулю при стремлении
в окрестности (2) начала координат и выполнены условия (3), тогда существует решение системы (1) удовлетворяющее условию (5) которая стремится к нулю при стремлении 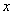 к нулю.
к нулю.
Литература:
1. А. А. Шестаков. Поведение интегральных кривых системы вида 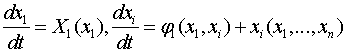 в окрестности особой точки. ДАН СССР. т.LX11.№ 5,стр.591–594, 1948 г.
в окрестности особой точки. ДАН СССР. т.LX11.№ 5,стр.591–594, 1948 г.
2. А. А. Шестаков. О поведении интегральных кривых системы дифференциальных уравнений в окрестности особой точки высшего порядка. ДАН СССР, т.LXV,№ 2,стр.139–142, 1949 г.
3. Д. М. Груз. Последовательные приближения для систем двух уравнений типа Брио и Буке. Исследования по дифференциальным уравнениям. Изд. АНУзССР. Ташкент, стр.40–46, 1963 г.







