Данная работа посвящена анализу влияния стратегий поведения исследователей на диффузионные потоки фундаментальных знаний. Диффузионные потоки знаний рассматриваются с позиции публикационной активности исследователей системы. В качестве носителя новых фундаментальных знаний рассматривается научная статья. Она же содержит ссылки автора на другие статьи, содержание которых использовалось автором при создании данной статьи. Количество данных ссылок считается мерой потока знаний переданных автору от исследователей, создавших данные знания. Иными словами, научные статьи (точнее их авторы) в данном исследовании выступают в качестве источников и реципиентов фундаментальных знаний. Диффузия знаний, то есть количество переданных знаний от источника к реципиенту измеряется количеством ссылок последнего на публикации статей источника. Величина диффузионных потоков во многом определяется стратегией, принятой реципиентом (или группой реципиентов) при проведении исследовательских работ. Если акторы-реципиенты ставят целью своей работы значительное расширение существующей базы знаний путем подхватывания уже известных результатов ИиР и их пошагового, инкрементального усовершенствования, то потоки диффузии, обеспечивающие данный процесс, могут быть весьма значительны. Если действия акторов-реципиентов направлены на получение знаний, радикально изменяющие ситуацию в данной области науки, то потоки диффузии знаний, необходимые для получения данных результатов не столь значительны, поскольку не существует или достаточно мало аналогов разрабатываемым результатам.
Реципиенты и источники знаний (акторы системы производства фундаментальных знаний) в данной работе объединены в укрупненные группы, сформированные по отраслям наук и мировым регионам. В качестве базы данных, определяющей продукты процесса производства знаний (публикации) и их диффузию, используется Web of Science.
При анализе процессов создания и диффузии знаний в отраслях наук, выделяются, в соответствии с методологией Web of Science, пять укрупненных научных отраслей: наука о жизни и биомедицина, естественные науки, технические и прикладные науки, искусство и гуманитарные науки, социальные науки. Для анализа пространственного распределения процессов рассматриваются следующие мировые регионы: Северная Америка, Западная Европа (15 стран Европейского союза со стажем), Восточная Европа, Тихоокеанский регион, Юго-восточная Азия и Япония (далее будем ссылаться на данный регион как регион Юго-Восточной Азии). Специальное внимание уделяется анализу российской и китайской системы производства новых знаний. Поэтому отдельно рассматриваются две страны — Россия и Китай. Чтобы выявить достоинства и недостатки стратегий акторов НИС этих стран производится бенчмаркинг, то есть сопоставление российских и китайских показателей процесса создания и диффузии знаний с соответствующими показателями мировых регионов.
1. Основные типы диффузии знаний как характеристики процесса создания новых знаний
При анализе статистических данных было установлено, что для ряда исследуемых объектов (акторов системы) характерен резкий рост интереса актов-исследователей к произведенным знаниям в первые 2–3 года после выхода публикаций. Этот рост достаточно быстро сменяется постепенным падением интереса исследователей к этим публикациям. Характер диффузионных процессов свидетельствует о постепенном исчерпании ценности соответствующих результатов для исследователей по тематике, заданной работами раннего периода. Примеры такой стратегии подхватывания первичных результатов ИиР дают ученые, занимающиеся проблемами физиологии. Динамика процесса подхватывания и распространения знаний по физиологии, произведенных в 1995 году, приведена на рис.1.
Возможен и другой вариант процесса подхватывания возникающих новых знаний. При реализации этого варианта первая волна интереса исследователей-акторов (аналогичная только что описанной) сменяется второй волной подхватывания и расширения первичных знаний. Иными словами, после некоторого падения интереса к знаниям, сформулированных в первичных публикациях, возрождается интерес к развитию этих знаний и начинают доминировать стратегии исследователей, направленные не на создание радикально новых знаний, а на распространение и инкрементальное совершенствование уже существующей базы знаний. Наличие такой второй волны динамики диффузионных потоков знаний характерно для гуманитарных наук, в частности социологии, где первая волна резкого роста интереса к первичным знаниям (в первые 2–3 года) сменяется вторичной волной подхватывания спустя 7–10 лет.
Приведенные эмпирические данные свидетельствуют о необходимость разработки и применения математических моделей подхватывания и диффузии новых знаний, способных отразить только что описанные типы стратегий акторов в процессах создания новых знаний.
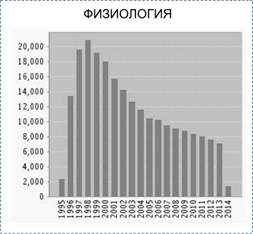
Рис. 1 Структура цитируемости знаний произведенных в 1995 году по физиологии
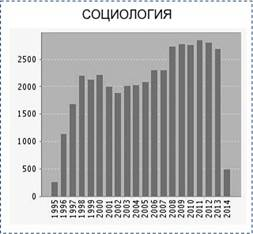
Рис. 2 Структура цитируемости знаний произведенных в 1995 году по социологии
Процессы диффузии новых знаний обладают многими чертами сходными с процессами диффузии инноваций. Класс диффузионных моделей в области инноваций достаточно широк [2]. В данной работе для построения базовой модели диффузии знаний используется однофакторная и двухфакторная диффузионная модели Басса [1], применение и развитие которых позволяет описать разных типов стратегий акторов-исследователей при создании новых знаний и характерные черты соответствующие им процессы распространения новых знаний, указанные выше.
Ниже при изложении моделей Басса в аспекте ее применения к распространению новых знаний предполагается, что существует два канала передачи информации о новых знаниях, формирующих соответственно первую и вторую волны интереса к первичным знаниям.
Используя первый из них пользователи (акторы-исследователи) получают новые знания из внешних первичных источников. В качестве первичных источников выступают научные статьи, обладающие высокой степенью новизны. При этом исследователи чаще всего выбирают источник новых знаний, исходя из его положительной репутации — известного имени автора публикации, или высокого импакт-фактора научного журнала. Акторы, которые пользуются этим каналом передачи информации, являются адаптаторами новых знаний. Если через некоторое время в среде исследователей после некоторого падения интереса к первичным знаниям не наблюдается появления новых акторов, деятельность которых направлена на дальнейшее распространение этих знаний, то процесс диффузии знаний на этом заканчивается. Для описания данного канала рационально использование однофакторной процесса Басса.
Если процесс диффузии знаний не затухает, то начинает действовать второй канал передачи знаний. В основе действия второго канала лежит вторичное использование знаний, переработанных адаптаторами. Класс исследователей-акторов, обеспечивающих действие второго канала, по сути, образуют имитаторы известных научных результатов, которые во многом повторяя уже известные результаты, пытаются их несколько усовершенствовать. Необходимо отметить, что имитаторы получают информацию о первичных знаниях в результате использования первого канала.
Что же касается взаимодействий между двумя типами акторов, то данная модель является ассиметричной, так как первый тип исследователей — адаптаторы оказывают влияние на второй тип — имитаторов, но не существует обратного взаимодействия. При этом стоит отметить принцип усиливающейся обратной связи — количество адаптаторов увеличивает поток новых имитаторов за счет эффекта межличностных коммуникаций.
Для описания последовательного действия двух каналов в большей степени подходить двухфакторная модель Басса.
2. Двухфакторная модель диффузии
Из рис.3 видно, что существует два локальных максимума цитируемости статей. Первый из них является результатом распространения нового знания среди исследователей-адаптаторов (передача информации о новом продукте осуществлялась посредством первого канала). Второй максимум образуется путем распространения новых знания среди исследователей-имитаторов.
Для более точного анализа перейдем к двухфакторной модели.
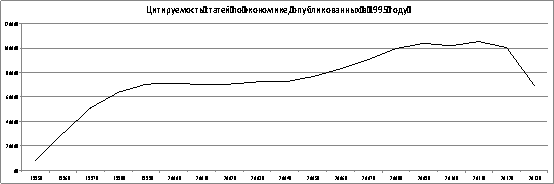
Рис. 3 Цитируемость статей по экономике, опубликованных в 1995 году
В двухфакторной модели Басса исследователи деляться на два класса — адаптаторы и имитаторы, а также данная модель определяет влияние первого класса исследователей на второй. В нижеприведенных формулах учитывается, что:
- фактор внутреннего влияния для адаптаторов q1=0;
- факторы внешнего влияния для адаптаторов и имитаторов одинаковы p1=p2=p;
- кумулятивное число ссылок на статьи, в которых могут использоваться новые знания m1+m2=m, где m1 — кумулятивное число ссылок на статьи, которые относятся к классу адаптаторов новых знаний; m2 — кумулятивное число ссылок на статьи, которые относятся к классу имитаторов новых знаний;
- число ссылок на статьи, в которых на момент t уже использовались новые знания N1(t)+N2(t)=N(t), где N1(t) — число ссылок на статьи, в которых к моменту t новые знания уже использовались адаптаторами; N2(t) — число ссылок на статьи, в которых к моменту t новые знания уже использовались имитаторами;
Динамика распространения новых знаний:
Адаптаторами 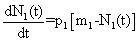 (1)
(1)
Имитаторами 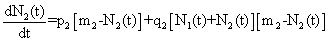 (2)
(2)
Прирост ссылок произведенных адаптаторами за момент времени t пропорционален вероятности появления нового знания у адаптаторов, а также количеству знаний произведенных адаптаторами за момент времени t. В то время как прирост ссылок совершенных имитаторами равен сумме адаптационных характеристик, когда знания получаются первым путем передачи информации, и имитационных характеристик.
Тогда общая формула распространения новых знаний:
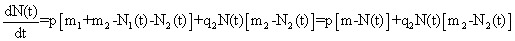 (3)
(3)
Таким образом суммарный прирост ссылок пропорционален кумулятивному адаптационному поведению как адаптаторов, так и имитаторов, а также имитационному поведению имитаторов.
На рис. 4 показано прогнозирование диффузии новых знаний адаптаторами и имитаторами с помощью двухфакторной модели Басса.
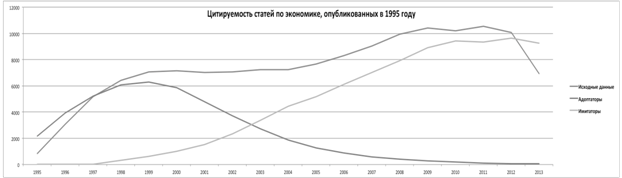
Рис. 4 Моделирование поведения адаптаторов и имитаторов на примере цитируемость статей по экономике, опубликованных в 1995 году
Данная модель (3) содержит три параметра (p, q, m), нахождение которых можно осуществить с помощью МНК [4]. Процедура МНК включает в себя оценку параметров путем дискретного или регрессионного аналога дифференциального уравнения (3) — (4): (где 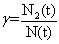 )
)
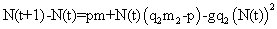 (4)
(4)
Тогда:
(5)
где a1=pm; a2=q2m2-p; a3=-γq2.
Использование МНК метода позволит выделить коэффициенты внутреннего (a1) и внешнего (a3) влияния без решения диффузионных уравнений для всех рассматриваемых объектов. Подразумевается, что параметры m и γ одинаковы внутри группы рассматриваемых объектов, поэтому для целей данной работы достаточно определить a1 и a3.
3. Выводы
В результате анализа модели были выделены адаптационные и имитационные параметры стратегий акторов системы производства фундаментальных знаний (отдельных ученых, отраслей наук, мировых регионов и т. д.)
Литература:
1. Bass F. M. A new product growth model for consumer durables // Management Science. 1969
2. Fareena Sultan, John U. Farley, Donald R. Lehmann A Meta-Analysis of Diffusion Models // Journal of Marketing Research. 1990.
3. Franses P. H. Forecasting in marketing. Econometric Institute Report EI 2004–40, EUR
4. Mahajan V., Muller E., Bass F. New Product Diffusion Models in Marketing: A Review and Directions for Research // Journal of Marketing. 1990. Vol. 54.







