Целью данной работы является моделирование синхронного неявнополюсного дугостаторного двигателя (СНДД) с помощью магнитных и электрических схем замещения [1], [2], [3]. Статорная (индукторная) обмотка представляет собой классическую трехфазную обмотку (Z1 = 6, m1 = 3, q = 1) с нулевым проводом, позволяющую построить корректную математическую модель системы «АИН ШИМ – синхронный неявнополюсный дугостаторный двигатель», которую представим в одной из следующих статей. Вследствие разомкнутости магнитопровода появится несимметрия в токах по фазам и ток в нулевом проводе. Кроме того, возникнет неподвижный в пространстве и пульсирующий во времени поток (продольный краевой эффект), влияние которого на электромагнитные процессы тем больше, чем выше скорость ротора. В данной работе обмотка индуктора питается от трехфазного синусоидального напряжения. Роторная обмотка состоит из шести катушек (Z2 = 12), соединенных последовательно (4-7, 5-8, 6-9, 10-1, 11-2 и 12-3). На начало 4-й катушки и конец провода 3-й катушки через кольца подается постоянное напряжение Uf (рис. 1). В данной работе рассматривается частотный пуск, поэтому напряжение постоянного тока в роторную обмотку подается раньше, чем на статорную обмотку. Частота подводимого напряжения на индуктор изменяется от 0 до конечного значения по пропорциональному закону, а модули трехфазного напряжения по параболическому закону (возможен пропорциональный закон), которые будут приведены ниже в самой математической модели. Данная работа адресована студентам, поэтому дана без сокращений.
Запишем основные уравнения для «n»-ого участка схемы замещения.
Баланс магнитных напряжений магнитной цепи
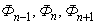– контурные магнитные потоки;
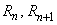– магнитные сопротивления воздушных участков;
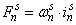– магнитодвижущая сила, созданная статорным током 
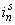, протекающим по всем проводникам паза (
);
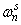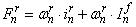– М.Д.С. тока в обмотке ротора;
– в шунтирующих зонах.
Баланс М.Д.С. для «n»-го участка имеет следующий вид:
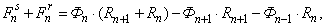
где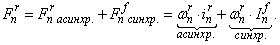 
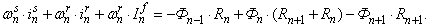
Ток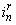 
условно назовем асинхронной составляющей полного тока в роторной обмотке. Этот ток создается от Э.Д.С. трансформации, Э.Д.С. движения, от изменяющегося потока во времени или от движущего потока в пространстве. При построении обобщенной математической модели двигателей, исключая вторую составляющую М.Д.С. 
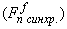с помощью соответствующих ключей, можно перейти к линейным (дугостаторным) асинхронным двигателям [5], [6], [7].
Вторая составляющая М.Д.С. (условно назовем синхронная составляющая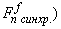 
представляет собой бегущую в пространстве ступенчатую фигуру в соответствии с дискретным расположением роторной обмотки.
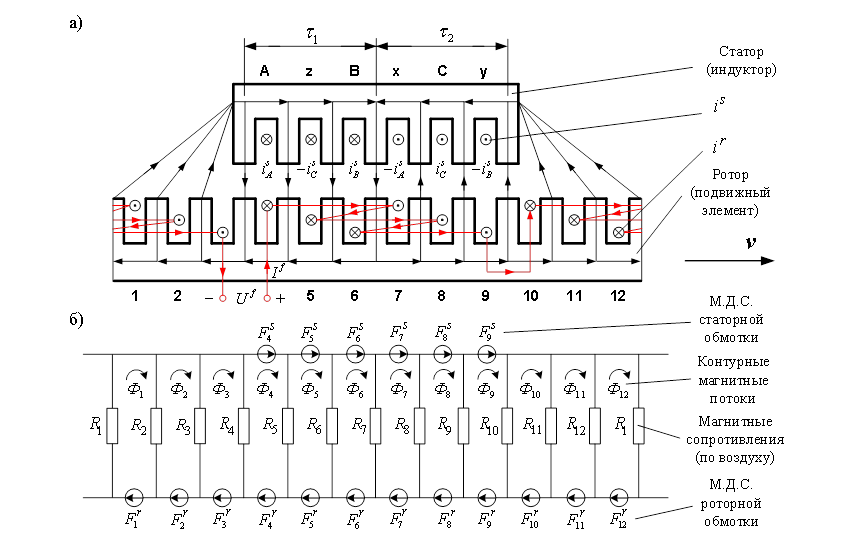
Рис. 2. а) Синхронный неявнополюсный дугостаторный двигатель (2р = 2, Z1 = 6); б) Магнитная схема замещения
В данной работе синхронную составляющую выразим 1-й гармоникой бегущей волны:
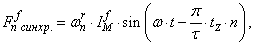
где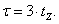 
Отсюда асинхронная составляющая тока в обмотке ротора определится по следующему выражению:
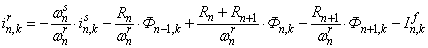. (1)
Уравнение баланса напряжений электрической цепи ротора для асинхронной составляющей тока ротора
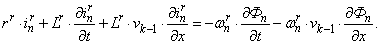(2)
Выразим производные во времени через конечные разности:
,
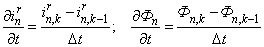где n – номер зубцового деления;
k – номер шага разбиения по времени.
В формуле (2) линейную скорость ротора принимаем равной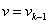 
и в пределах «k» интервала считается постоянным.
Производные по пространственной координате «х» выразим через центральные конечные разности:
.
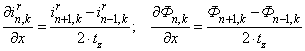С учетом вышеприведенных замечаний уравнение (2) примет следующий вид:
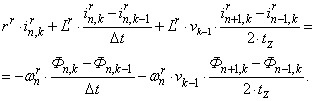(3)
Исключим из уравнения (3) асинхронную составляющую тока в роторе. Для этого подставим выражение (1) в уравнение (3) и получим:
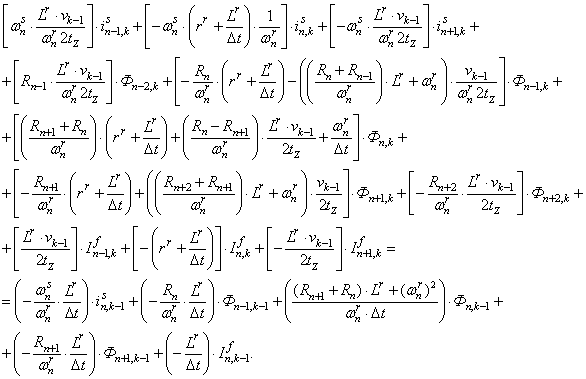(4)
Это уравнение может быть реализовано при произведении матрицы А, элементы которой записаны в квадратных скобках, на матрицу-столбец X, состоящей из потоков (Ф) и токов статорной обмотки. Правая часть уравнения (4) формирует первые двенадцать элементов матрицы-столбца свободных членовS в (k-1) момент времени. Элементы 13, 14 и 15 строк матрицы А и соответствующие элементы s13, s14 и s15 будут сформированы из баланса напряжений статорной обмотки.
Наконец, последние элементы матриц А и S определятся из баланса токов в трехфазной обмотке соединенной в звезду с нулевым проводом. Матрица-столбец Х сформирована из первых двенадцати элементов, соответствующих потокам Ф1, … , Ф12, а остальные – токам статорной обмотки iАs, iСs, iВs и i0s.
Общий вид матриц при числе полюсов 2р = 2 и общем числе пазов индуктора (статора) Z1 = 6 приведен на рис.3.
Введем следующие обозначения:
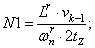
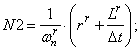
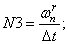
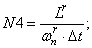
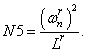
- Магнитные сопротивления в шунтирующих зонах:
R1 = 500∙Rδ;
R2 = R12 = 50∙Rδ;
R3 = R11 = 5∙Rδ.
- Магнитные сопротивления в индукторной зоне:
R4 = R5 = … = R10 = Rδ.
- Элементы матрицы А, перемножаемые на потоки матрицы-столбца Х:
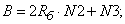
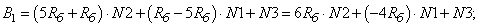
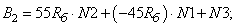
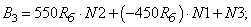
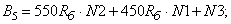
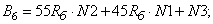
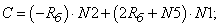
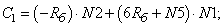
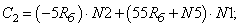
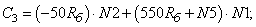
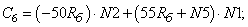
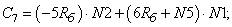
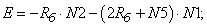
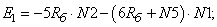
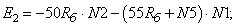
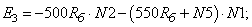
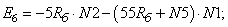
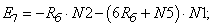
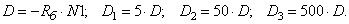
- Элементы матрицы А, перемножаемые на токи матрицы Х:
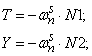
- Элементы матрицы-столбца свободных членов S:
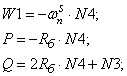
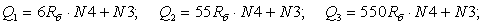
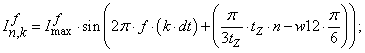
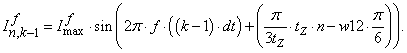
Уравнение (4) позволит определить для первых двенадцати строк элементы матрицы А и с первый по двенадцатый элементы матрицы-столбца S, для этого последовательно зададимся n:
n = 1.
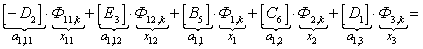
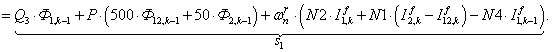
Запишем элементы матрицы А:
; 
; 
; 
; 
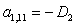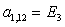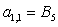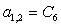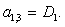
В правой части сформирован элемент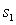 
матрицы-столбца S:
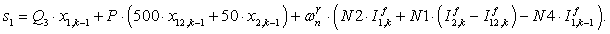
Примечание: вначале матрица А предстанет «пустой» и после каждой операции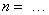 
определятся постепенно элементы для каждой строки и только в конце всех операций матрица А предстанет перед читателем в том виде как она дана на рис. 3. Но эта «пустая» матрица А уже должна быть подготовлена. Эта «пустая» форма направляет, выступает «организующим началом» по поиску элементов в каждой строке.
При n = 1, как было показано выше, определились элементы первой строки. Найденные коэффициенты вписываем в матрицу А. В дальнейшем становится понятным алгоритм заполнения матрицы.
|
Матрица А |
Х |
S |
|||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
||
|
1 |
a1,1 |
a1,2 |
a1,3 |
a1,11 |
a1,12 |
× |
x1 = Ф1 |
= |
s1 |
||||||||
|
2 |
a2,1 |
a2,2 |
a2,3 |
a2,4 |
a2,12 |
x2 = Ф2 |
s2 |
||||||||||
|
3 |
a3,1 |
a3,2 |
a3,3 |
a3,4 |
a3,5 |
a3,13 |
x3 = Ф3 |
s3 |
|||||||||
|
4 |
a4,2 |
a4,3 |
a4,4 |
a4,5 |
a4,6 |
a4,13 |
a4,14 |
x4 = Ф4 |
s4 |
||||||||
|
5 |
a5,3 |
a5,4 |
a5,5 |
a5,6 |
a5,7 |
a5,13 |
a5,14 |
a5,15 |
x5 = Ф5 |
s5 |
|||||||
|
6 |
a6,4 |
a6,5 |
a6,6 |
a6,7 |
a6,8 |
a6,13 |
a6,14 |
a6,15 |
x6 = Ф6 |
s6 |
|||||||
|
7 |
a7,5 |
a7,6 |
a7,7 |
a7,8 |
a7,9 |
a7,13 |
a7,14 |
a7,15 |
x7 = Ф7 |
s7 |
|||||||
|
8 |
a8,6 |
a8,7 |
a8,8 |
a8,9 |
a8,10 |
a8,13 |
a8,14 |
a8,15 |
x8 = Ф8 |
s8 |
|||||||
|
9 |
a9,7 |
a9,8 |
a9,9 |
a9,10 |
a9,11 |
a9,14 |
a9,15 |
x9 = Ф9 |
s9 |
||||||||
|
10 |
a10,8 |
a10,9 |
a10,10 |
a10,11 |
a10,12 |
a10,15 |
x10 = Ф10 |
s10 |
|||||||||
|
11 |
a11,1 |
a11,9 |
a11,10 |
a11,11 |
a11,12 |
x11 = Ф11 |
s11 |
||||||||||
|
12 |
a12,1 |
a12,2 |
a12,10 |
a12,11 |
a12,12 |
x12 = Ф12 |
s12 |
||||||||||
|
13 |
a13,4 |
a13,7 |
a13,13 |
x13 = iАS |
s13 |
||||||||||||
|
14 |
a14,6 |
a14,9 |
a14,15 |
x14 = iСS |
s14 |
||||||||||||
|
15 |
a15,5 |
a15,8 |
a15,14 |
x15 = iВS |
s15 |
||||||||||||
|
16 |
a16,13 |
a16,14 |
a16,15 |
a16,16 |
x16 = i0S |
s16 |
|||||||||||
Рис. 3. Общий вид матриц A, X и S.
n = 2.
; 
; 
; 
; 
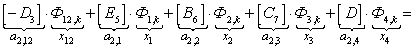
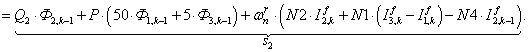
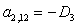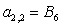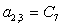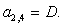
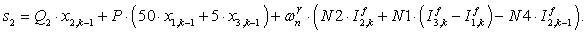
n = 3.
; 
; 
; 
; 
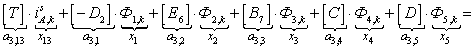
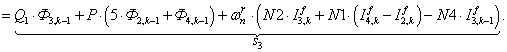
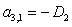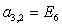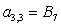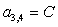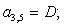
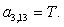
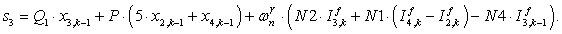
Примечание: при подстановке в уравнение (4) n = 4, мы увидим в соответствии с рис. 1, что войдет ток iСS с отрицательным знаком, в то же время в матрице-столбце Хнет знака «–» , поэтому его необходимо учесть в соответствующем элементе матрицы А.
Аналогично для других фаз, в концах обмоток x, y, z условно принимаем знак «–» и этот знак вводим в соответствующие элементы матрицы А.
n = 4.
; 
; 
; 
; 
; 
; 
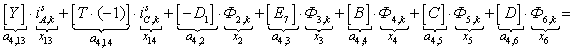
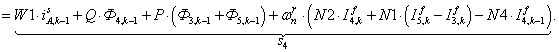
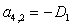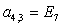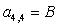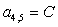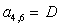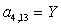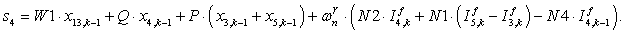
n = 5.
; 
; 
; 
; 
; 
;
; 
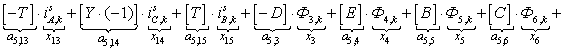
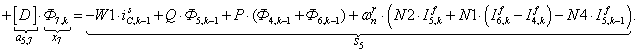
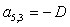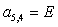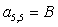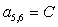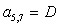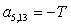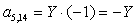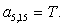
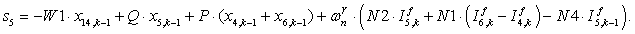
n = 6.
; 
; 
; 
; 
; 
;
; 
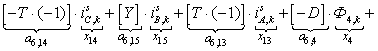
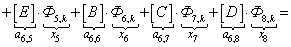
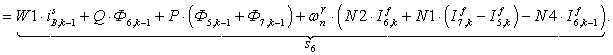
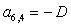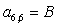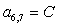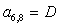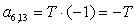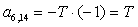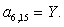
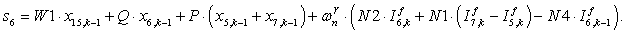
n = 7.
; 
; 
; 
; 
; 
;
; 
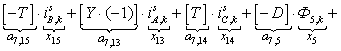
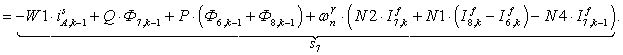
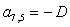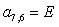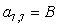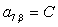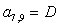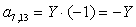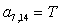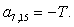
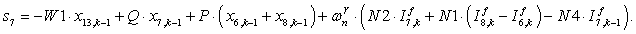
n = 8.
; 
; 
; 
; 
; 
;
; 
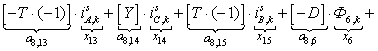
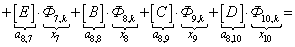
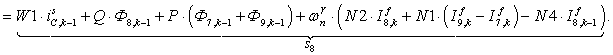
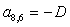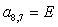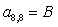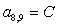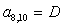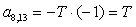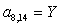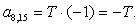
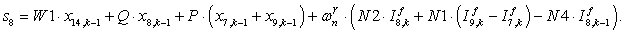
n = 9.
; 
; 
; 
; 
; 
; 
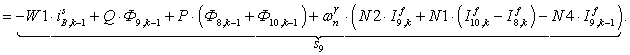
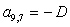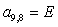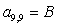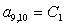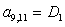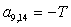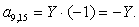
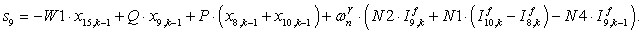
n = 10.
; 
; 
; 
; 
; 
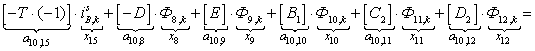
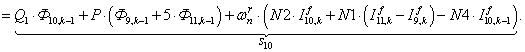
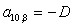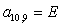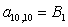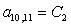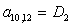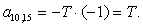
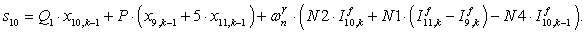
n = 11.
; 
; 
; 
; 
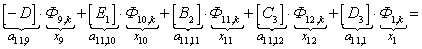
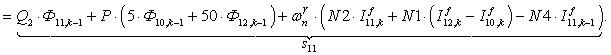
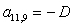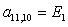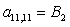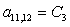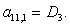
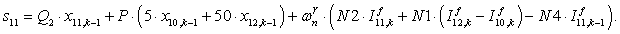
n = 12.
; 
; 
; 
; 
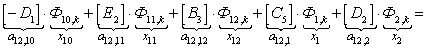
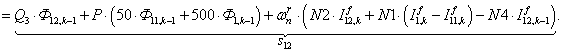
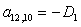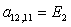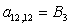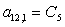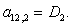
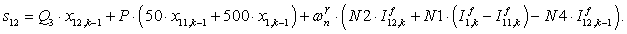
Элементы строк 13 и 14 и 15 матрицы А и соответствующие элементы матрицы-столбца S определяются из баланса электрических напряжений обмоток статора.
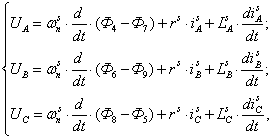(5)
где 
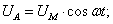
(6)
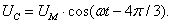
С учетом шага по времени ∆t в k-ый момент времени:
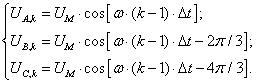(7)
n = 13.
Выразим производные тока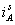 
, потоков 
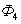и 
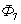через конечные разности:
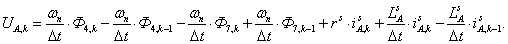
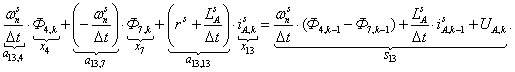
Обозначим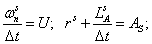 
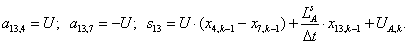
Аналогично для строк 14 и 15:
n = 14.
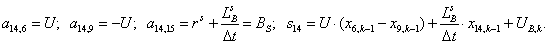
n = 15.
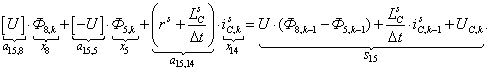
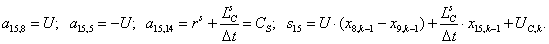
n = 16.
Наконец, сумма токов определяет элементы шестнадцатой строки матрицы А и элемент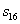 
матрицы-столбца S.
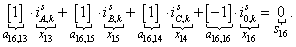
Окончательно, матрица А примет следующий вид, удобный для программирования в MATLAB (рис.4):
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
1 |
B5 |
C6 |
D1 |
-D2 |
E3 |
|||||||||||
|
2 |
E5 |
B6 |
C7 |
D |
-D3 |
|||||||||||
|
3 |
-D2 |
E6 |
B7 |
C |
D |
T |
||||||||||
|
4 |
-D1 |
E7 |
B |
C |
D |
Y |
-T |
|||||||||
|
5 |
-D |
E |
B |
C |
D |
-T |
-Y |
T |
||||||||
|
6 |
-D |
E |
B |
C |
D |
-T |
T |
Y |
||||||||
|
7 |
-D |
E |
B |
C |
D |
-Y |
T |
-T |
||||||||
|
8 |
-D |
E |
B |
C |
D |
T |
Y |
-T |
||||||||
|
9 |
-D |
E |
B |
C1 |
D1 |
-T |
-Y |
|||||||||
|
10 |
-D |
E |
B1 |
C2 |
D2 |
T |
||||||||||
|
11 |
D3 |
-D |
E1 |
B2 |
C3 |
|||||||||||
|
12 |
C5 |
D2 |
-D1 |
E2 |
B3 |
|||||||||||
|
13 |
U |
-U |
AS |
|||||||||||||
|
14 |
U |
-U |
BS |
|||||||||||||
|
15 |
-U |
U |
CS |
|||||||||||||
|
16 |
1 |
1 |
1 |
-1 |
Рис. 4
Неизвестные переменные (потоки и токи в статорной обмотке) в k-й момент времени определяются в результате следующей операции с матрицами:
X=A-1·S,
Далее, подставляя в уравнение (1) n = 1…12, определяем суммарные токи в роторе:
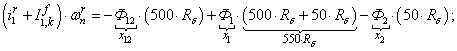
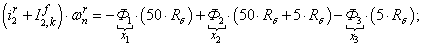
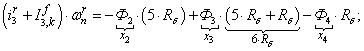
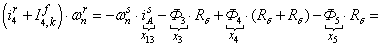
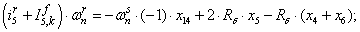
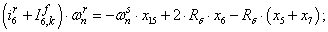
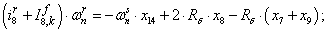
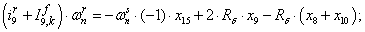
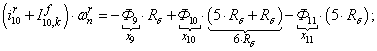
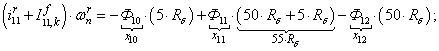
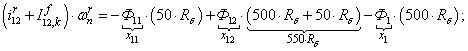
Электромагнитные усилия на зубцовом делении определяются по следующим формулам:
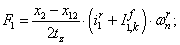
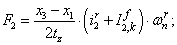
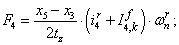
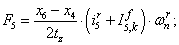
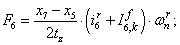
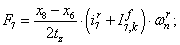
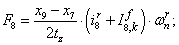
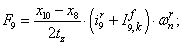
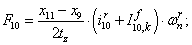
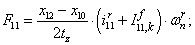
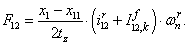
Суммарное усилие: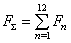 
.
Линейная скорость ротора в k-й момент времени: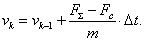 
Математическая модель синхронного неявнополюсного дугостаторного двигателя реализована в программном пакете MATLAB методом Гаусса-Жордана. Ниже приведен пример расчета.
% Математическая модель СНДД с укладкой статорной обмотки классическим
% способом (z=6) с нулевым проводом
% function lad_z12_6_zero
% Исходные данные синхронного двигателя
Rb=0.1003*10^7;
rs=9.98;
LsA=0.22;
LsB=0.23;
LsC=0.21;
rr=47.25;
Lr=0.18;
dt=0.001;
As=rs+LsA/dt;
Bs=rs+LsB/dt;
Cs=rs+LsC/dt;
tz=9.769*10^-3;
m=2.66;
v0=0;
wns=200;
wnr=1200;
UA=wns/dt;
X=zeros(16,1);
F=0;
Ufm=65;
Ifm=Ufm/rr;
w12=1.12;
mass_Um = 0;
mass_f = 0;
mass_t = 0;
tk=8;
Ukon=80;
Unach=3;
K=input('Длительность цикла k=');
for k=1:(K+1)
if ((k*dt >= 0) && (k*dt <=tk))
fc = k*dt*45/tk;
w=2*pi*fc;
Um = Unach+(Ukon-Unach)*((k*dt)^1.6)/((tk)^1.6);
end;
if (k*dt > tk)
fc=45+5*((tanh(k*dt-1)^0.6))*0;
w=2*pi*fc;
Um = Ukon+10*((tanh(k*dt-1)^0.6))*0;
end;
if ((k*dt >= 0) && (k*dt <= 5))
Fc = 0;
end;
if (k*dt > 5)
Fc=0;
end;
v(1,k)=v0; % Создание вектор-строки для графика скорости
f(1,k)=sum(F)-Fc; % Создание вектор-строки для графика усилия
Ua=Um*cos(w*(k-1)*dt);
Ub=Um*cos(w*(k-1)*dt-2*pi/3);
Uc=Um*cos(w*(k-1)*dt-4*pi/3);
i0(1,k)=X(16);
i_a(1,k)=X(13);
i_b(1,k)=X(15);
i_c(1,k)=X(14);
% Формирование матрицы А
A=zeros(16);
N1=Lr*v0/(wnr*2*tz);
N2=(rr+Lr/dt)/wnr;
N3=wnr/dt;
N4=Lr/(wnr*dt);
N5=(wnr^2)/Lr;
B=2*Rb*N2+N3;
B1=6*Rb*N2-4*Rb*N1+N3;
B2=55*Rb*N2-45*Rb*N1+N3;
B3=550*Rb*N2-450*Rb*N1+N3;
B5=550*Rb*N2+450*Rb*N1+N3;
B6=55*Rb*N2+45*Rb*N1+N3;
B7=6*Rb*N2+4*Rb*N1+N3;
C=-Rb*N2+(2*Rb+N5)*N1;
C1=-Rb*N2+(6*Rb+N5)*N1;
C2=-5*Rb*N2+(55*Rb+N5)*N1;
C3=-50*Rb*N2+(550*Rb+N5)*N1;
C5=-500*Rb*N2+(550*Rb+N5)*N1;
C6=-50*Rb*N2+(55*Rb+N5)*N1;
C7=-5*Rb*N2+(6*Rb+N5)*N1;
D=-Rb*N1;
D1=5*D;
D2=50*D;
D3=500*D;
E=-Rb*N2-(2*Rb+N5)*N1;
E1=-5*Rb*N2-(6*Rb+N5)*N1;
E2=-50*Rb*N2-(55*Rb+N5)*N1;
E3=-500*Rb*N2-(550*Rb+N5)*N1;
E5=-50*Rb*N2-(550*Rb+N5)*N1;
E6=-5*Rb*N2-(55*Rb+N5)*N1;
E7=-Rb*N2-(6*Rb+N5)*N1;
T=-wns*N1;
Y=-wns*N2;
for n=1:12
If(n)=Ifm*sin(w*k*dt+((pi/3)*n-w12*pi/6));
end;
for n=1:12
If1(n)=Ifm*sin(w*(k-1)*dt+((pi/3)*n-w12*pi/6));
end;
W1=-wns*N4;
P=-Rb*N4;
Q=2*Rb*N4+N3;
Q1=6*Rb*N4+N3;
Q2=55*Rb*N4+N3;
Q3=550*Rb*N4+N3;
for n=1:3
A(n+2,n+12)=(-1)^(n+1)*T;
A(n+3,n+12)=(-1)^(n+1)*Y;
A(n+4,n+12)=(-1)^n*T;
A(n+5,n+12)=(-1)^n*T;
A(n+6,n+12)=(-1)^n*Y;
A(n+7,n+12)=(-1)^(n+1)*T;
end;
for n=1:3
A(16,n+12)=1;%hh
end;
A(16,16)=-1;%jgj
for n=1:6
A(n+3,n+3)=B;
A(n+4,n+3)=E;
A(n+2,n+3)=C;
end;
for n=1:7
A(n+1,n+3)=D;
A(n+4,n+2)=-D;
end;
A(1,1)=B5;
A(1,2)=C6;
A(1,3)=D1;
A(1,11)=-D2;
A(1,12)=E3;
A(2,1)=E5;
A(2,2)=B6;
A(2,3)=C7;
A(2,12)=-D3;
A(3,1)=-D2;
A(3,2)=E6;
A(3,3)=B7;
A(4,2)=-D1;
A(4,3)=E7;
A(9,10)=C1;
A(9,11)=D1;
A(10,10)=B1;
A(10,11)=C2;
A(10,12)=D2;
A(11,1)=D3;
A(11,10)=E1;
A(11,11)=B2;
A(11,12)=C3;
A(12,1)=C5;
A(12,2)=D2;
A(12,10)=-D1;
A(12,11)=E2;
A(12,12)=B3;
A(13,4)=UA;
A(14,6)=UA;
A(15,8)=UA;
A(13,7)=-UA;
A(14,9)=-UA;
A(15,5)=-UA;
A(13,13)=As;
A(14,15)=Bs;
A(15,14)=Cs;
% Матрица свободных членов
S=[ Q3*X(1)+P*(500*X(12)+50*X(2))+wnr*N2*If(1)+wnr*N1*(If(2)-If(12))-wnr*N4*If1(1); %1
Q2*X(2)+P*(50*X(1)+5*X(3))+wnr*N2*If(2)+wnr*N1*(If(3)-If(1))-wnr*N4*If1(2); %2
Q1*X(3)+P*(5*X(2)+X(4))+wnr*N2*If(3)+wnr*N1*(If(4)-If(2))-wnr*N4*If1(3); %3
W1*X(13)+Q*X(4)+P*(X(3)+X(5))+wnr*N2*If(4)+wnr*N1*(If(5)-If(3))-wnr*N4*If1(4); %4
(-1)*W1*X(14)+Q*X(5)+P*(X(4)+X(6))+wnr*N2*If(5)+wnr*N1*(If(6)-If(4))-wnr*N4*If1(5); %5
W1*X(15)+Q*X(6)+P*(X(5)+X(7))+wnr*N2*If(6)+wnr*N1*(If(7)-If(5))-wnr*N4*If1(6); %6
(-1)*W1*X(13)+Q*X(7)+P*(X(6)+X(8))+wnr*N2*If(7)+wnr*N1*(If(8)-If(6))-wnr*N4*If1(7); %7
W1*X(14)+Q*X(8)+P*(X(7)+X(9))+wnr*N2*If(8)+wnr*N1*(If(9)-If(7))-wnr*N4*If1(8); %8
(-1)*W1*X(15)+Q*X(9)+P*(X(8)+X(10))+wnr*N2*If(9)+wnr*N1*(If(10)-If(8))-wnr*N4*If1(9); %9
Q1*X(10)+P*(X(9)+5*X(11))+wnr*N2*If(10)+wnr*N1*(If(11)-If(9))-wnr*N4*If1(10); %10
Q2*X(11)+P*(5*X(10)+50*X(12))+wnr*N2*If(11)+wnr*N1*(If(12)-If(10))-wnr*N4*If1(11); %11
Q3*X(12)+P*(50*X(11)+500*X(1))+wnr*N2*If(12)+wnr*N1*(If(1)-If(11))-wnr*N4*If1(12); %12
UA*(X(4)-X(7))+(LsA/dt)*X(13)+Ua; %13
UA*(X(6)-X(9))+(LsB/dt)*X(15)+Ub; %14
UA*(X(8)-X(5))+(LsC/dt)*X(14)+Uc; %15
0]; %16
% Решение методом Гаусса-Жордана
Z=rref([A S]); %Приведение расширенной матрицы к треугольному виду
X=Z(1:16,17:17); %Выделение последнего столбца из матрицы
% Ток в роторе
IR=[ Rb*(550*X(1)-50*X(2)-500*X(12)); %1
Rb*(55*X(2)-5*X(3)-50*X(1)); %2
Rb*(6*X(3)-X(4)-X(2)); %3
(-wns*X(13)+Rb*(2*X(4)-X(5)-X(3))); %4
((-1)*(-wns)*X(14)+Rb*(2*X(5)-X(6)-X(4))); %5
(-wns*X(15)+Rb*(2*X(6)-X(7)-X(5))); %6
((-1)*(-wns)*X(13)+Rb*(2*X(7)-X(8)-X(6))); %7
(-wns*X(14)+Rb*(2*X(8)-X(9)-X(7))); %8
((-1)*(-wns)*X(15)+Rb*(2*X(9)-X(10)-X(8))); %9
Rb*(6*X(10)-5*X(11)-X(9)); %10
Rb*(55*X(11)-50*X(12)-5*X(10)); %11
Rb*(550*X(12)-500*X(1)-50*X(11))]; %12
% Электромагнитное усилие
F(1)=(X(2)-X(12))*(IR(1))/(2*tz);
for n=1:10
F(n+1)=(X(n+2)-X(n))*(IR(n+1))/(2*tz);
end;
F(12)=(X(1)-X(11))*(IR(12))/(2*tz);
% Скорость
v0=v0+((sum(F)-Fc)/m)*dt;
mass_Um(k)=Um;
mass_fc(k)=fc;
mass_t(k)=k*dt;
end;
% Построение графиков
figure(1);
plot(mass_t,mass_Um,'r',mass_t,mass_fc,'b');
grid on;
axis([0 10 0 100]);
figure(2);
k=0:K;
subplot(2,1,1);
plot(k*dt,v);
title('Скорость');
xlabel('t,c');
ylabel('v,m/c');
grid on;
subplot(2,1,2);
plot(k*dt,f);
title('Сила');
xlabel('t,c');
ylabel('F,H');
grid on;
%end
Временные зависимости скорости и электромагнитного усилия синхронного неявнополюсного дугостаторного двигателя в режиме частотного пуска, полученные на математической модели при Ufm = 65 (80 и 100) В, представлены на рис. 5–10.
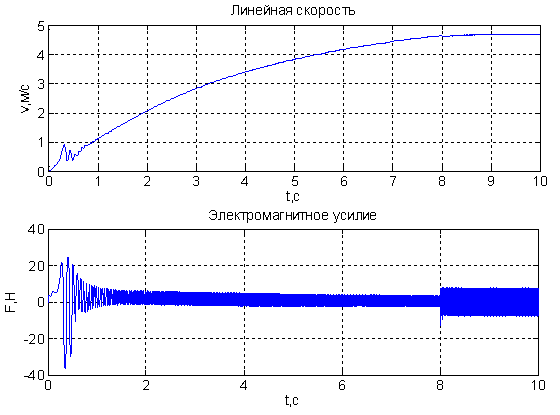
Рис. 5. Результат моделирования синхронного неявнополюсного дугостаторного двигателя в режиме частотного пуска при Ufm = 65 В
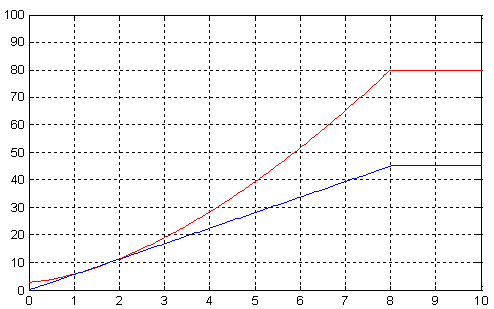
Рис. 6. Изменение напряжения Um и частоты f при частотном пуске с напряжением Ufm = 65 В
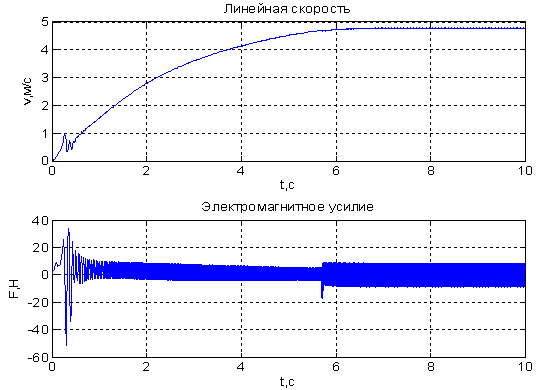
Рис. 7. Результат моделирования синхронного неявнополюсного дугостаторного двигателя в режиме частотного пуска при Ufm = 80 В
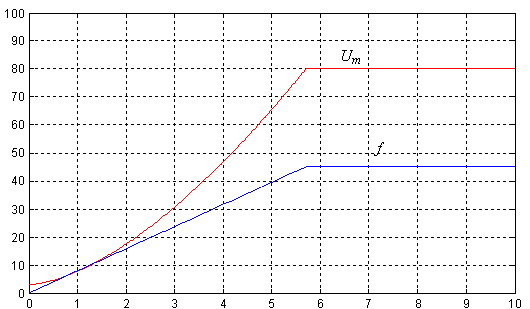
Рис. 8. Изменение напряжения Um и частоты f при частотном пуске с напряжением Ufm = 80 В
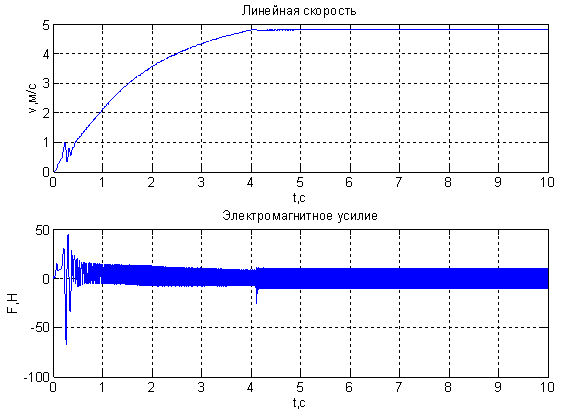
Рис. 9. Результат моделирования синхронного неявнополюсного дугостаторного двигателя в режиме частотного пуска при Ufm = 100 В
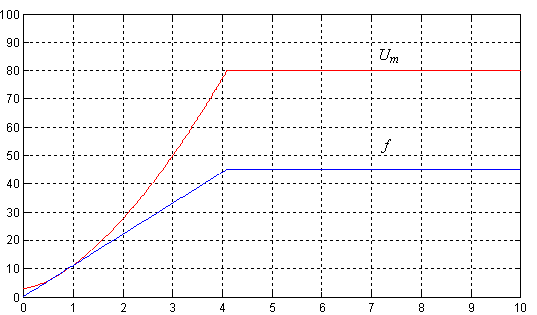
Рис. 10. Изменение напряжения Um и частоты f при частотном пуске с напряжением Ufm = 100 В
Данная модель позволяет легко смоделировать прямой пуск асинхронного дугостаторного двигателя [4], [5], [6] и [7], для этого необходимо задать Ufm= 0, f = 45 Гц и Um = 80 В. Соответствующие пункты в математической модели с законами f(t) и Um(t) необходимо закомментировать (рис. 11).
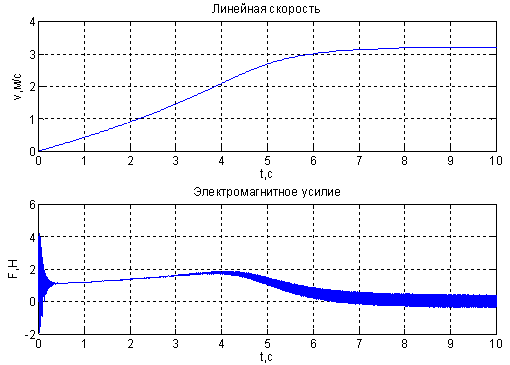
Рис. 11. Результат моделирования асинхронного дугостаторного двигателя в режиме прямого пуска при Um = 80 В и f = 45 Гц
Результаты расчетов СНДД потока Ф и М.Д.С.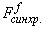 
в различные моменты времени в установившемся режиме с напряжением Ufm= 80 (проверка на синхронность), рис. 12 и рис. 13.
|
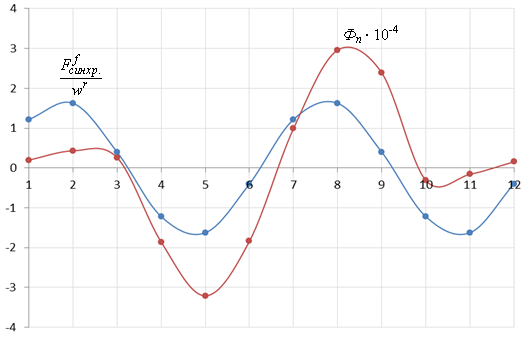
Рис. 12. Результат моделирования СНДД в установившемся режиме при Ufm= 80 В и k = 7000
|
|
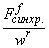
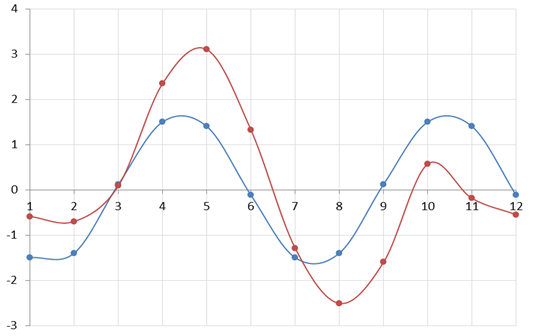
Рис. 13. Результат моделирования СНДД в установившемся режиме при Ufm= 80 В и k = 6990
Зависимости токов ,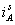 
, 
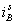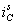и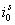 
даны на рис. 14.
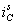
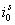
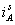
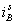
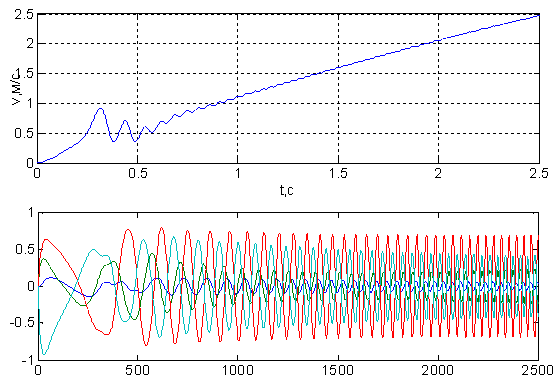
Рис. 14. Временные зависимост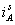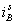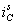и , , и 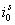при k = 2500
Литература:
1. Веселовский О.Н. и др. Линейные асинхронные двигатели / Веселовский О.Н., Коняев А.Ю., Сарапулов Ф.Н. – М.: Энергоатомиздат, 1991. – 256 с.
2. Емельянов А.А., Богатов Е.А., Клишин А.В., Медведев А.В., Симонович В.Г. Математическая модель линейного асинхронного двигателя на основе магнитных схем замещения // Молодой ученый. – 2010. - №5. – С. 14-22.
3. Емельянов А.А., Медведев А.В., Богатов Е.А., Кобзев А.В., Бочкарев Ю.П. Программирование линейного асинхронного двигателя в MATLAB // Молодой ученый. – 2013. - №3. – С. 129-143.
4. Емельянов А. А., Медведев А. В., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Киряков Г.А., Чернов М.В., Габзалилов Э.Ф., Иванин А.Ю. Программирование линейного асинхронного двигателя с числом пазов в индукторе равном шесть // Молодой ученый. – 2013 –. № 10 – С. 23-38.
5. Емельянов А. А., Медведев А. В., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Киряков Г.А., Чернов М.В., Габзалилов Э.Ф., Иванин А.Ю. Моделирование линейного асинхронного двигателя с укладкой обмотки индуктора (Z1=6) через спинку ярма // Молодой ученый. – 2013 –. № 10 –С. 39-54.
6. Емельянов А.А., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Бочкарев Ю.П., Авдеев А.С., Киряков Г.А., Чернов М.В., Габзалилов Э.Ф., Иванин А.Ю. Программирование линейного асинхронного двигателя (Z1 = 6) с трехфазной обмоткой индуктора с нулевым проводом // Молодой ученый. – 2014. – №2. – С. 36-51.
7. Емельянов А.А., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Габзалилов Э.Ф., Киряков Г.А. Моделирование системы АИН ШИМ — линейный асинхронный двигатель (Z1 = 6) с классическим типом обмотки с нулевым проводом // Молодой ученый. – 2014. – №6(65,май). – С. 24-43.
