В статье анализируется изгиб линейной части трубопровода, возникающий при ударных нагрузках. Предложена модель поперечных перемещений заглубленного трубопровода, которая позволяет оценить параметры импульсной ударной нагрузки.
Ключевые слова: воздействие взрывной нагрузки, нагрузки на трубопровод, поперечные перемещения трубопровода.
При воздействии ударной импульсной нагрузки на заглубленные сооружения (трубопроводы) обычно выделяют три типа деформации:
изгиб линейной части;
продольное перемещение;
смятие цилиндрических диаметров линейной части.
В статье анализируется второй тип деформаций, возникающий достаточно часто даже при средних ударных нагрузках, если эпицентр её приложения попадает в некоторую критическую зону вблизи заглубленного трубопровода. При превышении допустимых нагрузок и пределов текучести материала трубопровода такие деформации приводят к трещинообразованию в его линейной части и, как следствие, техногенным авариям.
Целесообразно рассмотреть две модели продольных деформаций трубопровода:
без учёта рассеивание ударной энергии в материале трубопровода;
с учетом влияния рассеивания ударной энергии.
При составлении этих моделей полагаем:
трубопровод заглублен в грунт на 1–2 метра, что позволяет рассматривать плоскостную задачу, имеющую меньшую сложность по сравнению с объёмной задачей;
координатная ось (абсцисс) направлена вдоль условной оси бесконечного трубопровода;
начало координат находится в точке пересечения оси с перпендикуляром, опущенным из эпицентра приложения ударной импульсной нагрузки.
Дифференциальное уравнение вынужденных продольных перемещений «бесконечного» трубопровода при воздействии на него взрывной волны записывается в виде [1]:
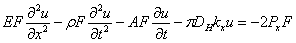 , (1)
, (1)
где 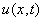 — перемещение поперечного сечения трубопровода на расстояние x от начала координат в момент времени t;
— перемещение поперечного сечения трубопровода на расстояние x от начала координат в момент времени t; 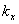 — коэффициент касательного сопротивления грунта;
— коэффициент касательного сопротивления грунта; 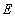 — модуль упругости материала;
— модуль упругости материала; 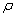 — плотность материала;
— плотность материала; 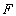 — площадь поперечного сечения;
— площадь поперечного сечения; 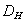 - наружный диаметр трубопровода,
- наружный диаметр трубопровода, 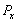 — проекция нагрузки вдоль оси трубопровода.
— проекция нагрузки вдоль оси трубопровода.
Предполагается, что между контактными касательными напряжениями 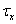 и осевыми перемещениями
и осевыми перемещениями 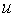 существует линейная зависимость, т. е.
существует линейная зависимость, т. е.
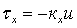 .
.
Возможность использование линейной зависимости подтверждается экспериментальными данными [2].
Значение коэффициента 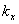 определяется свойствами грунта. Для приближённых расчётов рекомендованы следующие значения:
определяется свойствами грунта. Для приближённых расчётов рекомендованы следующие значения:
для грунтов малой плотности — 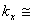 0,3 кг/см3;
0,3 кг/см3;
средней плотности — 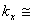 1 кг/см3;
1 кг/см3;
повышенной плотности -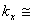 2 кг/см3.
2 кг/см3.
Продольные деформации сопровождаются также поперечными деформациями, т. е. изменением поперечных сечений при удлинении трубопровода. Однако, при воздействии волн, длина которых значительно превышает размеры поперечных сечений трубопровода, этими изменениями можно пренебречь [3].
Скорости распространения волн в материале стальных труб отличаются от скоростей распространения волн в грунте. В нашей модели предполагается, что при прохождении взрывного импульса по стальному трубопроводу до точки х, грунт в этой точке ещё неподвижен.
Вследствие симметрии деформации трубопровода в упругой среде под воздействием взрывной волны рассмотрим только на положительной полуоси.
Учитывая, что в начальный момент трубопровод находится в покое, зададим граничные условия:
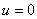 при
при 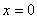 ;
;
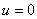 при
при 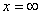 ,
,
а также начальные условия при 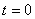 :
:
u = 0; 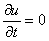 . (2)
. (2)
Уравнение (1) запишем в виде:
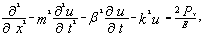 (3)
(3)
где 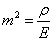 ;
; 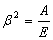 ;
; 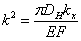 .
.
Для решения уравнения (3) с граничными и начальными условиями (2) применим косинус-преобразование Фурье.
Для функции 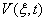 получим дифференциальное уравнение:
получим дифференциальное уравнение:
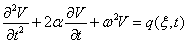 (4)
(4)
при начальных условиях 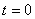 :
:
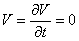 ,
,
где 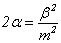 ;
; 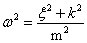 ;
;
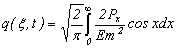 . (5)
. (5)
Из полученных уравнений (4) и (5) видно, что если известен закон распределения нагрузки во времени, то можно получить решение для вычисления деформаций, распределенных по длине трубопровода. При кратковременном воздействии импульсной нагрузки, используя дельта-функцию Дирака и проинтегрировав (5), получим
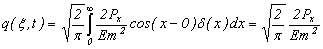 . (6)
. (6)
Проекцию взрывной ударной нагрузки Рх на ось х, вызывающей продольные деформации трубопровода, определим из известного соотношения:
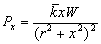 , (7)
, (7)
где W — приведенная мощность взрывного импульса, 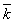 - коэффициент, зависящий от свойства грунта, r — расстояние от эпицентра приложения взрывного импульса.
- коэффициент, зависящий от свойства грунта, r — расстояние от эпицентра приложения взрывного импульса.
Решением уравнения (4) является сумма общего решения однородного линейного дифференциального уравнения и частного решения неоднородного дифференциального уравнения с постоянными коэффициентами.
Учитывая, что деформация трубопровода достигает максимального значения в конце воздействия ударной нагрузки (т. е. при 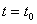 ), для продольных перемещениях трубопровода получим:
), для продольных перемещениях трубопровода получим:
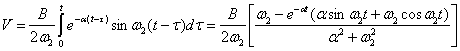 ; (8)
; (8)
где 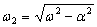 ;
;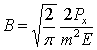 .
.
Используя формулу обращения косинус-преобразования Фурье, получим:
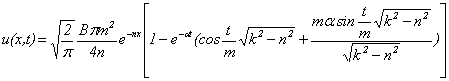 , (9)
, (9)
где 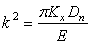 ,
, 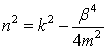 .
.
В полученной модели (9) первый член представляет продольное смещение «полубесконечного» трубопровода, лежащего в грунте на Винклеровом основании при статическом действии нагрузки. Динамический коэффициент смещения, в первом приближении, можно считать постоянным, не зависящим от инерционных свойств или массы трубопровода [4].
После дифференцирования уравнения (9) по переменной x, получим напряжения растяжения (сжатия):
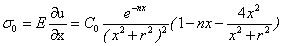 ; (10)
; (10)
где Со — некоторый коэффициент в частном решении неоднородного дифференциального уравнения, вычисляемый по формуле:
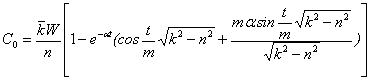 . (11)
. (11)
В вышеприведенной модели продольных деформаций трубопровода (9, 10) не учитывалось рассеивание энергии в материале трубопровода.
Рассмотрим модель продольных деформаций трубопровода с учетом влияния рассеивания энергии взрывной ударной нагрузки.
Предположим, что диссипация энергии в материале трубопровода зависит только от продолжительности взрывного импульса и свойств материала трубопровода. Исследование влияния рассеяния энергии в материале трубопровода проведено с учетом зависимости напряжения от деформации материала трубопровода Кельвина-Фохта:
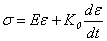 ,
,
где 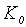 − коэффициент вязкости, ε — относительная деформация материала трубопровода.
− коэффициент вязкости, ε — относительная деформация материала трубопровода.
С учетом затухания энергии рассеивания дифференциальное уравнение продольных смещений подземного трубопровода примет вид:
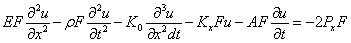 . (12).
. (12).
Для решения уравнения (12) выполним математические выкладки аналогичные ранее приведенным. Получим следующие соотношения для вычисления смещения трубопровода:
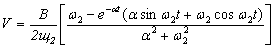 ;
;
где 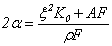 ;
; 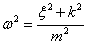 ;
; 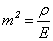 ;
; 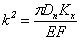 ;
; 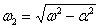 .
.
По формуле обращения косинус-преобразования Фурье получим:
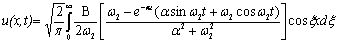 (13)
(13)
Для вычисления интеграла разобьем выражение (13) на три интеграла.
Первый интеграл, описывающий статическую деформацию трубопровода, примет вид:
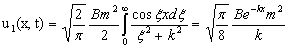 .
.
Второй интеграл
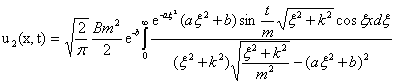 ,
,
где 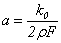 ;
; 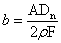 ,
,
имеет главную часть на участке от нуля до единицы, далее его подынтегральная функция быстро убывает, так как наличие экспоненты с отрицательной степенью в подынтегральном выражении приводит к тому, что величина интеграла в дальнейшем становится незначительной. По этой причине вторым интегралом можно пренебречь.
При вычислении третьего интеграла:
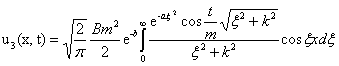 ,
,
учтем, что в него входят быстро осциллирующие функции, которые делают достаточно сложным его аналитическое вычисление.
Окончательное вычисление продольного смещения заглубленного трубопровода под воздействием ударной импульсной нагрузки можно выполнить только численными методами исходя из следующей формулы:
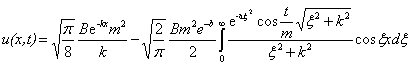 . (14)
. (14)
Для определения максимальных значений продольных напряжений вычислим интеграл при х=0. Продифференцировав уравнение (14) по переменной x и разложив подынтегральную функцию в ряд по функциям Бесселя, получим продольное напряжение в точке х=0 с учетом рассеивания энергии в материале трубопровода:
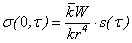 , (15)
, (15)
где s(τ) — функция времени, параметров трубопровода и среды, предварительно вычисляемая по следующей формуле:
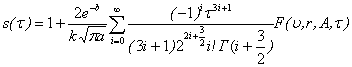 , (16)
, (16)
где 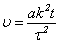 ,
, 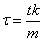 ,.
,. 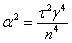 ,
, 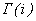 -гамма-функция,
-гамма-функция, 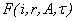 – обобщенная, функция, полученная на основе гипер-геометрической, с параметрами, зависящими от индекса суммирования, жесткости трубопровода и акустического сопротивления грунта.
– обобщенная, функция, полученная на основе гипер-геометрической, с параметрами, зависящими от индекса суммирования, жесткости трубопровода и акустического сопротивления грунта.
Ряд в функции (16) сходится достаточно быстро, и для ее вычисления достаточно взять 3–4 члена ряда.
На рисунке 1 приведены зависимости максимальных значений напряжений продольного перемещения от расстояний до эпицентра приложения взрывной нагрузки:
сплошной линией отображена зависимость без учета рассеяния энергии взрывной нагрузки в материале трубопровода;
пунктирной линией отображена аналогичная зависимость с учетом рассеяния энергии взрывной нагрузки;
точками отображены величины напряжений, полученные экспериментальным путем.
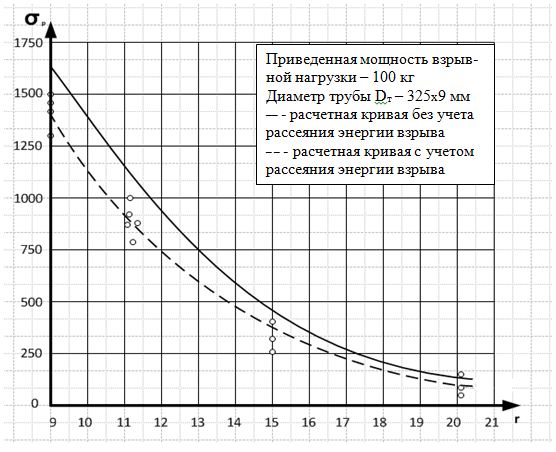
Рис. 1. График зависимостей продольных напряжений σр в заглубленном трубопроводе от расстояний r до эпицентра взрывной нагрузки
При построении графиков расчеты выполнены для магистрального трубопровода диаметром 325 мм с толщиной стенок 9 мм. Вычисление нагрузки произведено по формуле (7), при зависящих от свойств грунта значениях коэффициентов 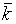 и
и 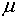 , типичных для большинства областейевропейской части РФ.
, типичных для большинства областейевропейской части РФ.
В полученном решении (15), позволяющем найти продольные напряжения трубопровода, учитывается рассеяние энергии в материале трубопровода.
Из приведенных графиков видно, что экспериментальные точки расположены несколько ниже расчетной кривой, полученной по формулам (10) и достаточно близко к расчетной кривой (15), что свидетельствует о фактическом рассеивании энергии взрывной нагрузки в материале трубопровода.
Рассмотренные модели продольных перемещений заглубленного трубопровода с учетом и без учета рассеивания энергии взрывной нагрузки в материале трубопровода являются адекватными экспериментальным данным, т. к. результаты расчетов в достаточной степени согласуется с ними.
Полученные соотношения (9, 10, 14, 15) позволяют оценить критические параметры внешней нагрузки, приводящей к продольным перемещениям трубопровода и деформациям, при которых достигаются пределы текучести, возникает усталость материала оболочки и происходит трещинообразование в линейной части трубопровода под воздействием импульсных ударных нагрузок.
Литература:
1. Мавлютов Р. М. Исследование поражаемости и напряженного состояния магистральных нефтепродуктопроводов при проведении взрывов: дисс. … канд.техн.наук. — Уфа: УГНТУ, 1971.
2. Большаков Ю. Н. Разработка метода демонтажа трубопроводов энергией взрыва: дисс. … канд.техн.наук. — Тюмень, 2004.
3. Садовский М. А. Механическое действие воздушных ударных волн по данным экспериментальных исследований// Сб.Физика взрыва. — М.: Изд-во АН СССР, 1952.
4. Ляхов Г. М. Основы динамики взрывов в грунтах и жидких средах. — М.:Недра, 1964.
5. Взрывные явления. Оценка и последствия: в 2 кн./У.Бейкер, П.Кокс, П.Уэстайн [и др.]; пер. с англ. — М.: Мир, 1986.







