Одна из целей современной высшей школы — дать студентам не только общую, но и профессиональную подготовку, необходимую базу для самообразования, применения знаний в реальных производственных проблемах.
Изучение курса «Оптимизационные задачи в экономике» позволяет будущему экономисту просчитывать последствия тех или иных решений, прогнозировать развитие событий. В связи с этим основной задачей изучения дисциплины является обучение основам знаний, необходимым для решения оптимизационных задач в области экономики. Будущий специалист должен знать основы математического моделирования и уметь составлять математические модели оптимизационных задач.
При изучении данного курса рассматриваются темы: линейного программирования, динамического программирования, сетевого моделирования.
Предложенные алгоритмы решения алгоритмы могут быть использованы для анализа следующих задач:
1) задача максимизации или минимизации производственной функции при наличии ограничений;
2) задача производственного планирования;
3) задача об оптимальном соотношении ингредиентов смеси;
4) транспортная задача;
5) задача о назначениях;
6) задача о распределении инвестиций;
7) задача о замене оборудования;
8) задача о кратчайшем пути;
9) задача оптимизации временных параметров сетевых графиков.
Изучаемые примеры экономических задач носят схематический характер. Реальные задачи, безусловно, имеют больший объем исходных данных и требуют трудоемкого анализа, поэтому их решение возможно лишь с помощью компьютера. Показать возможности моделирования, проследить основные этапы анализа легче на упрощенных моделях. Это дает возможность в сложной ситуации грамотно формализовать цель и необходимые ограничения на рассматриваемые факторы экономического процесса, адекватно интерпретировать математический итог решения задачи, особенно, если алгоритм дает неопределенный или противоречивый ответ.
Рассмотрим пример решения задачи на минимум издержек от эксплуатации оборудования.
Найти оптимальный план замены оборудования на пятилетний период, если известны:
- прибыль от эксплуатации оборудования 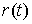 в зависимости от возраста;
в зависимости от возраста;
- остаточная стоимость 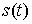 оборудования в зависимости от возраста;
оборудования в зависимости от возраста;
- стоимость нового оборудования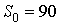 .
.
|
Возраст |
0 новое |
1 |
2 |
3 |
4 |
5 |
|
Прибыль |
70 |
70 |
65 |
40 |
30 |
|
|
Остаточная стоимость |
70 |
60 |
40 |
30 |
20 |
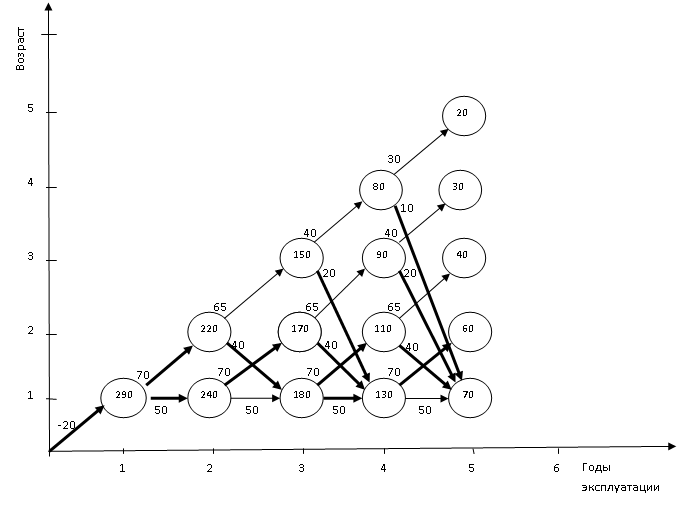
Рис. 1
По выделенным стрелкам видны три оптимальные траектории (рис. 2, 3, 4).
Траектория рис. 2 означает следующее оптимальное управление по годам:
|
Год |
1 |
2 |
3 |
4 |
5 |
|
Управление |
сохраняем |
обновляем |
сохраняем |
обновляем |
продаем |
Траектория рис. 3 означает следующее оптимальное управление по годам:
|
Год |
1 |
2 |
3 |
4 |
5 |
|
Управление |
обновляем |
сохраняем |
обновляем |
сохраняем |
продаем |
Траектория рис. 4 означает следующее оптимальное управление по годам:
|
Год |
1 |
2 |
3 |
4 |
5 |
|
Управление |
сохраняем |
обновляем |
обновляем |
сохраняем |
продаем |
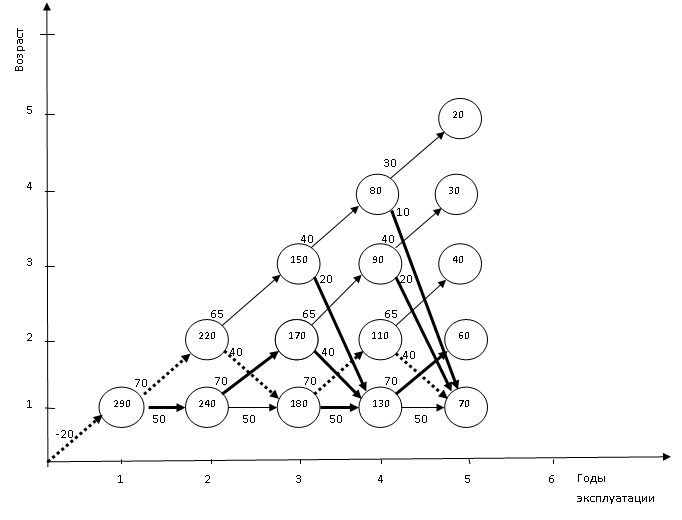
Рис. 2
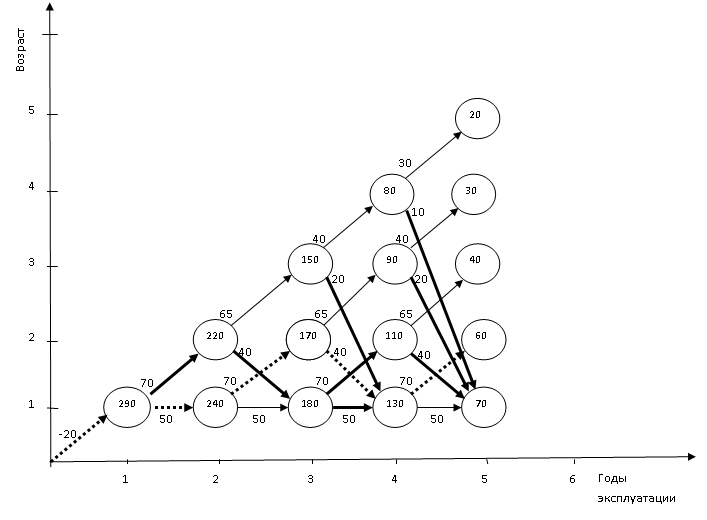
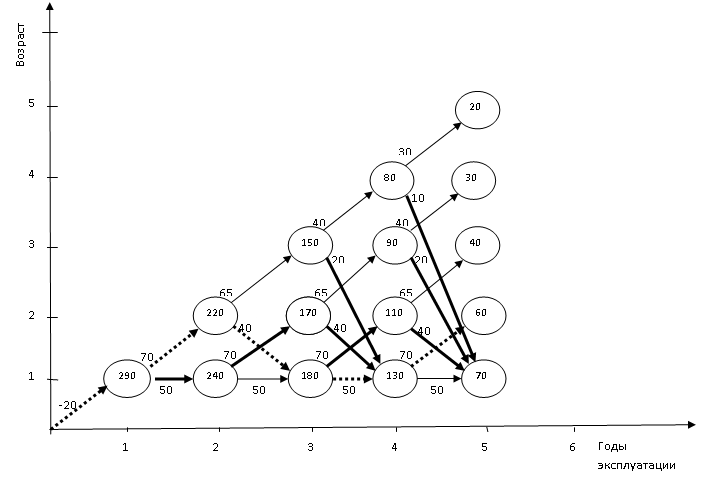 Рис. 3
Рис. 3
Рис. 4
В рассмотренной выше задаче выделяются три оптимальные траектории. И для принятия оптимального решения студентам, будущим экономистам необходимы знания методов исследования операций. Овладение методами логико-математического анализа решения оптимизационных задач позволяет отсеивать заведомо худшие варианты решения сложных ситуаций, предохраняя тем самым от грубых экономических ошибок в профессиональной деятельности. Кроме того, процесс формализации задачи выявляет дополнительную информацию, на основе которой множество альтернатив может быть сужено, что увеличивает шансы на правильный выбор оптимальной стратегии. Таким образом, овладение методами решения оптимизационных экономических задач позволяет глубже проникнуть в суть изучаемой проблемы и способствует развитию способностей, необходимых в дальнейшей профессиональной деятельности.
Литература:
1. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Профессиональная подготовка строителей через решение математических задач // Современные проблемы науки и образования. — 2014. — № 2. — С.168.
2. Куимова К. А. К вопросу преподавания дисциплины «Спецглавы математики» [Текст] / К. А. Куимова, Е. И. Куимова, С. Н. Ячинова // Молодой ученый. — 2014. — № 4. — С.1011–1014.
3. Ячинова С. Н. Мотивация обучения студентов посредством моделирования [Текст] / С. Н. Ячинова, В. С. Гудкова // Молодой ученый. — 2014. — № 4. — С.1141–1144.







