В статье рассматривается, как с помощью компьютерной модели интерференции когерентных волн от двух точечных источников, предлагаемой автором, демонстрируется зависимость интерференционной картины (распределения интенсивности результирующей волны вдоль отрезка прямой) от расстояния до источников волн.
Ключевые слова:визуализация, компьютерная визуализация, компьютерное моделирование, модель, учебная компьютерная модель, интерференция, когерентные волны, опыт Юнга.
Эта статья является логическим продолжением нашей статьи, опубликованной ранее [2], и конкретизирует некоторые результаты, представленные в других работах [3; 4; 5; 6; 13; 14; 15; 18; 19; 20]. Она наглядно демонстрирует, как с помощью компьютерного моделирования можно визуализировать учебные модели, описываемые математическими соотношениями [8; 9], дополняя их образными моделями [2; 3; 5; 6; 11] и другой графической информацией [1; 4; 7; 10; 12; 16; 17]. В предыдущей статье [2] кратко описывается методика демонстрации явления интерференции от двух точечных источников когерентных волн [3; 6; 17; 18]. В ней также приводится формула для расчета ширины максимумов интенсивности результирующей волны (рис. 1):
Δx= xk+1 — xk= yλ / d, k = 0, ±1, ±2, …,
где k — номер интерференционного максимума, y — расстояние от отрезка, соединяющего источники волн; λ — длина волны; d — расстояние между источниками. Выражение получено аналитически, при этом считалось, что расстояние y >> d. Именно, исходя из этого, на графике зависимости интенсивности I(x) интерферируемой волны максимумы интенсивности имеют одинаковую ширину. Кроме того, формула позволяет сделать вывод, согласно которому при удалении от источников ширина интерференционного максимума увеличивается пропорционально расстоянию y от картины распределения до отрезка d, соединяющего источники (коэффициент пропорциональности равен λ/d). Если же рассматривать картину между источниками, то вдоль отрезка, соединяющего источники, картина качественно будет такой же, какой она изображена на рис. 1 в его верхней части.
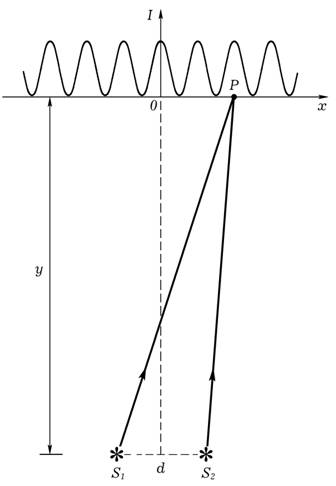
Рис. 1. Схема опыта Юнга, используемая для расчета приближенной интерференционной картины
Компьютерная модель явления строилась на том основании, что точечные источники испускают когерентные гармонические волны, которые являются сферическими (фронт волны представляет собой сферу). Такая модель является более точной, в сравнении с приближением, представленным выше и согласно которому наблюдаемая картина распределения интенсивности находится очень далеко от источников волн (в этом случае волны можно было бы считать плоскими). Полученное при компьютерном моделировании распределение интенсивности интерферируемой волны на плоскости (рис. 2) позволяет обучающимся сразу увидеть, как изменяется вид распределения по мере удаления от источников волн. Для количественной оценки на экран выводится еще и распределение интенсивности результирующей волны вдоль прямой, которое расположено в верхней части окна приложения (рис. 2).
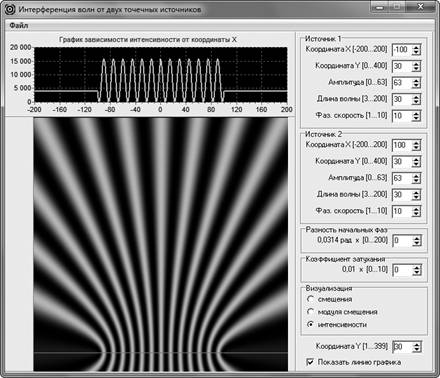
Рис. 2. Распределения интенсивности интерферируемой волны вдоль прямой, проходящей через источники волн, и на плоскости
По мере удаления от источников прямой, вдоль которой получается график зависимости I(x), картина распределения интенсивности вдоль этой прямой изменяется, что видно при сравнении рис. 2 и рис. 3. И чем дальше эта прямая от источников (рис. 4), тем больше распределение похоже на то, что получено аналитически (рис. 1). Таким образом компьютерная модель демонстрирует обучающимся «приближенность» учебной теории интерференции. Рассматривая распределения, показанные на рис. 2, рис. 3 и рис. 4, можно показать учащимся увеличение ширины максимума интерференционной картины по мере удаления наблюдаемой картины от источников волн, отличное от ожидаемого согласно теории. Например, на рис. 4 расстояние от картины распределения, представленной в верхней части окна приложения, до источников в три раза больше, чем на рис. 3. Обучающиеся могут легко заметить, что ширина центрального (нулевого) максимума интенсивности на рис. 4 при этом примерно в два раза больше (а не в три, как «предсказывает» фрагмент теории, приведенный в начале статьи).
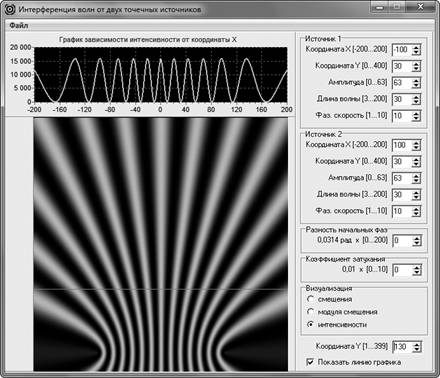
Рис. 3. Вид распределения интенсивности интерферируемой волны вдоль прямой, проходящей на некотором удалении от источников волн и параллельной прямой, проходящей через эти источники
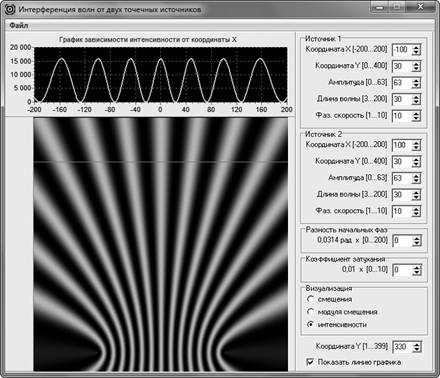
Рис. 4. Изменение вида распределения интенсивности интерферируемой волны вдоль прямой при удалении этой прямой от источников волн
Очень важно, чтобы преподаватель сообщил обучающимся, что и компьютерная модель не является «точным отображением» реальной интерференции, так как построена на математических (абстрактных) моделях. Например, интерферирующие волны являются гармоническими, испускающие их источники — точечными, а вокруг них отсутствуют какие-либо объекты. Среда, в которой распространяются волны, однородна и изотропна. Создать такие условия в реальной учебном физическом эксперименте невозможно [1; 7; 10; 124 14; 16; 17]. Можно только создать условия, более или менее близкие к этим условиям (волны являются почти гармоническими; среда — почти изотропная и однородная; объекты, расположенные вокруг, влияют на результаты экспериментов незначительно, размеры источников волн малы и т. п.). Поэтому также важно, чтобы учащиеся наблюдали результаты не только вычислительного, но и соответствующего натурного учебного эксперимента, и видели различие между реальным объектом исследования и его компьютерной моделью [2; 3; 6; 18].
Литература:
1. Данилов О. Е. Демонстрационный эксперимент по изучению звуковых полей методом компьютерного сканирования / О. Е. Данилов // Педагогика: традиции и инновации: материалы IV междунар. науч. конф. (г. Челябинск, декабрь 2013 г.). — Челябинск: Два комсомольца, 2013. — С. 209–212.
2. Данилов О. Е. Демонстрация явления интерференции волн от двух точечных источников с помощью компьютерной модели / О. Е. Данилов // Молодой ученый. — 2014. — № 13. — С. 5–10.
3. Данилов О. Е. Изучение интерференции с помощью компьютерного моделирования / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 9. — С. 50–58.
4. Данилов О. Е. Использование компьютерных моделей при обучении физике / О. Е. Данилов // Проблемы школьного и дошкольного образования: Материалы III регионального науч.-практ. семинара «Достижения науки и практики — в деятельность образовательных учреждений». — Глазов: Глазов. гос. пед. ин-т, 2012. — С. 101–102.
5. Данилов О. Е. Компьютерная визуализация распределений физических величин в пространстве / О. Е. Данилов // Молодой ученый. — 2013. — № 11. — С. 582–587.
6. Данилов О. Е. Компьютерная модель интерференции от двух точечных источников / О. Е. Данилов // Информатика: проблемы, методология, технологии: Материалы XI Международной научно-практической конференции, Воронеж, 10–11 февраля 2011 г.: в 3 т. Т. 3. Школа-конференция «Информатика в образовании». — Воронеж: Издательско-полиграфический центр Воронежского государственного университета, 2011. — С. 87–89.
7. Данилов О. Е. Компьютерная экспериментальная установка для сканирования полей физических величин / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2014. — № 1. — С. 77–80.
8. Данилов О. Е. Компьютерное моделирование: Волновое уравнение. Численные методы решения физических задач. Borland Pascal. Учебно-методическое пособие / О. Е. Данилов. — Глазов: ГГПИ, 2009. — 24 с.
9. Данилов О. Е. Компьютерное моделирование колебательного движения. Численные методы решения задач: учебно-методическое пособие / О. Е. Данилов, А. Ю. Трефилова. — Глазов: Глазов. гос. пед. ин-т, 2012. — 36 с.
10. Данилов О. Е. Метод компьютерного сканирования полей физических величин и его применение в учебном физическом эксперименте / О. Е. Данилов // Актуальные задачи педагогики: материалы V междунар. науч. конф. (г. Чита, апрель 2014 г.). — Чита: Издательство «Молодой ученый», 2014. — С. 231–235.
11. Данилов О. Е. Обучение компьютерному моделированию на примере создания компьютерной модели кругового математического маятника / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 10. — С. 80–87.
12. Данилов О. Е. Педагогические исследования по доказательству эффективности применения метода компьютерного сканирования полей при обучении физике / О. Е. Данилов // Инновации в образовании. — 2014. — № 6. — С. 147–158.
13. Данилов О. Е. Применение имитационного моделирования механических взаимодействий при обучении физике / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2014. — № 5. — С. 97–103.
14. Данилов О. Е. Принципы использования метода компьютерного сканирования полей физических величин в учебном процессе / О. Е. Данилов // Актуальные вопросы современной педагогики: материалы IV междунар. науч. конф. (г. Уфа, ноябрь 2013 г.). — Уфа: Лето, 2013. — С. 220–222.
15. Данилов О. Е. Формирование умения проводить теоретическое исследование при изучении распределения физической величины в пространстве с помощью компьютерной модели / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 7. — С. 84–94.
16. Данилов О. Е. Экспериментальное изучение интерференции звука на зеркале Ллойда с помощью компьютерных технологий / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2014. — № 4. — С. 89–94.
17. Данилов О. Е. Экспериментальное изучение явления интерференции с помощью метода сканирования полей физических величин / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 11. — С. 105–115.
18. Компьютерная модель интерференции / О. Е. Данилов. — Электрон. дан. — Сайты Google, 2011. — Режим доступа: https://sites.google.com/site/intercommod/. — Загл. с экрана.
19. Профессиональное образование: модернизационные аспекты: коллективная монография. В 9 т. Т. 4. / Р. М. Абдулгалимов, Н. А. Артеменко, С. В. Белоусов, Т, Е. Беньковская, О. М. Бородулина, О. Е. Данилов, С. И. Моднов, Т. К. Ивашковская, А. Г. Маланов, М. В. Пац, Н. В. Попова, Н. Е. Попова, Е. И. Черкашина; под ред. О. П. Чигишевой. — Ростов-н/Д: Издательство Международного исследовательского центра «Научное сотрудничество», 2014. — 267 с.
20. Danilov O. Particular didactic principles on the use of computer visualization of the fields of physical quantities in the educational process / O. Danilov // Young Scientist USA: Education. — Lulu, 2014. — P. 29–32.







