Кремний является одним из перспективных материалов микроэлектроники. В последние годы интенсивно исследуются физические свойства различных наноструктур на основе кремния и германия [1–12].
Важной задачей является расчет электрон — дырочных спектров наночастиц кремния погруженный в широкозонной диэлектрик, например в SiO2. Для расчета электронного спектра необходимо учитывать специфики зоны: многодолинности, анизотропию масс электронов и. т.д., а валентная зона является сильно вырожденным. В подобных структурах поглощение света связано с переходом электронов и дырок в дискретных уровнях, что может быть использовано для создания фотоприёмников [13].
Теоретические расчеты электронно-дырочных спектров в приближении эффективной массы проведены во многих работах, например, на основе теории возмущений [14,15], или численным методом [16] применительно квантовой точки (КТ) Si-SiO2 сферической формы.
В данной работе приведены результаты расчетов несколько нижних электронных уровней КТ Si-SiO2, где, сфера заменяется “моделирующим кубом” (т. е. квантовым ящиком). Учтены конечности высоты потенциальных барьеров, анизотропию и скачок массы электронов на границе гетероперехода Si-SiO2. Междолинное перемешивание не учитывалось. Значение полученных энергетических уровней сравниваются с результатами других авторов.
Уравнение Шредингера (УШ) для электрона вблизи “X ” долины имеет вид

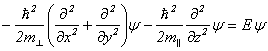 (1)
(1)
Если предположить, что КТ имеет кубическую форму, то переменные в УШ разделяется и требуется решать одномерной задачи (рис.1).
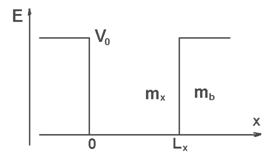
Рис.1. Профиль потенциала гетероперехода по оси x, энергия отсчитывается от дна ямы
Гамильтониан, описывающий движение электрона по оси x имеет вид
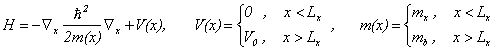 (2)
(2)
Здесь 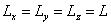 — ребра куба,
— ребра куба, 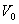 - высота потенциального барьера на границе гетероперехода Si-SiO2,
- высота потенциального барьера на границе гетероперехода Si-SiO2, 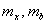 - масса электрона в зоне проводимости наночастиц Si и в запрещенной зоне SiO2 соответственно. Процедура решение задачи (2) (без учёта скачок массы) приведен во многих учебниках, см. например [17], которые в области I,II,III имеют вид
- масса электрона в зоне проводимости наночастиц Si и в запрещенной зоне SiO2 соответственно. Процедура решение задачи (2) (без учёта скачок массы) приведен во многих учебниках, см. например [17], которые в области I,II,III имеют вид
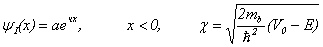 (3)
(3)
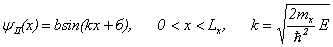 (4)
(4)
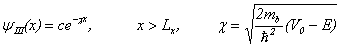 (5)
(5)
Граничные условия в точках 0 и 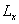 (условия Бастарда) имеют вид
(условия Бастарда) имеют вид
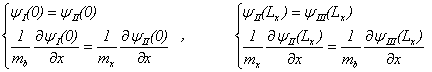 (6)
(6)
Поставляя сюда (3)-(5) и после некоторых упрощений получаем
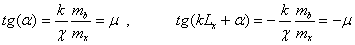 (7)
(7)
Исключив a из системы (7) и учитывая периодичность функций, получаем
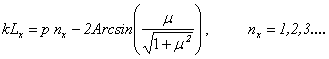 (8)
(8)
Это уравнение можно обобщить для других направлений и переписать так
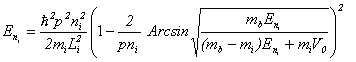 (9)
(9)
Здесь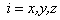 . В пределе равных масс
. В пределе равных масс 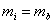 из (9) получается известное трансцендентное уравнение [17]. Хотя, для одномерного движения частиц в потенциальной яме всегда существуют связанного состояния, условия связывания частиц в трехмерной яме определяется как
из (9) получается известное трансцендентное уравнение [17]. Хотя, для одномерного движения частиц в потенциальной яме всегда существуют связанного состояния, условия связывания частиц в трехмерной яме определяется как
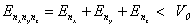 (10)
(10)
Если приближенно заменить сферы с эквивалентным кубом (равные объёмы), то
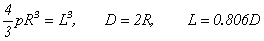 (11)
(11)
Согласно [14,15] 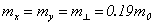 ,
, 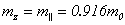 ,
, 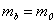 ,
,  .
.
Численно решая уравнение (9) с учетом (10) (11) можно определить зависимость значения энергетических уровней 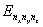 от диаметра сферы
от диаметра сферы 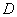 . Результаты расчетов представлены на рис.2.
. Результаты расчетов представлены на рис.2.
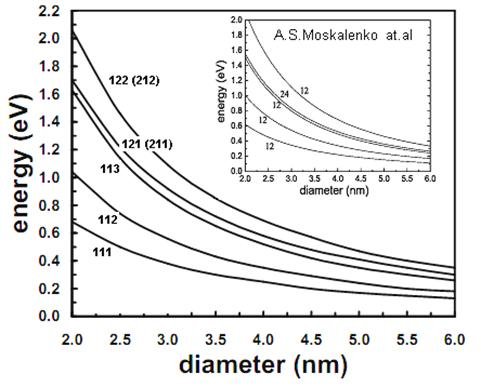
Рис.2. Зависимость положение энергетических уровней электрона от диаметра сферы
Цифры означают значений квантовых чисел nx, ny, nz. Энергетические уровни вырождены по {nx, ny}, так как 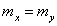 . На вставке показан результат численного решения дифференциального уравнение (1) внутри сферической КТ Si-SiO2 из работы [16]. Видно, что для нижних уровней результаты сходится.
. На вставке показан результат численного решения дифференциального уравнение (1) внутри сферической КТ Si-SiO2 из работы [16]. Видно, что для нижних уровней результаты сходится.
Обычно, в реальных условиях КТ не являются, идеально сферическими. По этой причине, для приближенного расчета энергетических уровней (в рамке принятых выше приближений) можно пользоваться методом квантового ящика.
Литература:
1. L. Pavesi, L. Dal Negro, C. Mazzoleni, G. Franzo, and F. Priolo, Nature (London) 408, 440 (2000).
2. M. V. Wolkin, J. Jorne, P. M. Fauchet, G. Allan, and C. Delerue, Phys. Rev. Lett. 82, 197 (1999).
3. M. Zacharias and P. M. Fauchet, Appl. Phys. Lett. 71, 380 (1997).
4. S. Takeoka, M. Fujii, S. Hayashi, and K. Yamamoto, Phys. Rev. B58, 7921 (1998).
5. L. T. Canham, Appl. Phys. Lett. 57, 1046 (1990).
6. A. Puzder, A. J. Williamson, J. C. Grossman, and G. Galli, Phys. Rev. Lett. 88, 097401 (2002).
7. P. D. J. Calcott, K. J. Nash, L. T. Canham, M. J. Kane, and D. Brumhead, J. Phys.: Condens. Matter 5, L91 (1993).
8. M. L. Brongersma, P. G. Kik, A. Polman, K. S. Min, and H. Atwater, Appl. Phys. Lett. 76, 351 (2000).
9. A. Y. Kobitski, K. S. Zhuravlev, H. P. Wagner, and D. R. T Zahn, Phys. Rev. B 63, 115423 (2001).
10. D. Kovalev, H. Heckler, G. Polisski, and F. Koch, Phys. Status Solidi B 215, 871 (1999).
11. F. A. Reboredo, A. Franceschetti, and A. Zunger, Phys. Rev. B 61, 13 073 (2000).
12. C. Delerue, M. Lannoo, and G. Allan, Phys. Rev. Lett. 84, 2457 (2000).
13. K. Brunner, Rep. Progr. Phys. 65, 27 (2002).
14. В. А. Бурдов. ЖЭТФ 121, 480–488, (2002)
15. В. А. Бурдов. ФТП 36, 1233–1236, (2002)
16. A. S. Moskalenko, J. Berakdar, A. A. Prokofiev and I. N. Yassievich. Phys. Rev. B 76, 085427 (2007).
17. Л. Д. Ландау, Е. М. Лифшиц. Квантовая механика (М., Наука, 1989).







