Математическая модель классификации состава выпускаемых изделий с использованием экспертных методов

В сегодняшнее время существуют разные математические методы [6] для решения задачи управления торговли, подбора товаров на разных уровнях предприятий.

Из проведенного анализа зарубежных и отечественных разработок в области математического моделирования вытекает: разработка математических методов в определении качества выпускаемых изделий должна формироваться по этапной схеме. Автоматизация формирования множества признаков товаров однородных по смыслу их качеств, разработка критериев, формирование резерва выпуска изделий из сформированных множества товаров. Ниже сформулирован первый этап разработки математических методов в определения качества выпускаемых изделий.

Уровень развития производства (предприятий, объединений, ведомость) зависит от качественного состава выпускаемых изделий. Качественный состав выпускаемых изделий — это такой аспект развития производства, который в числе других факторов обеспечивает выполнение спроса потребителей. Этот аспект описывается различными признаками, которые относятся к отдельному виду товаров, имеющихся в производстве. На основе этого набора признаков сформулируем задачу классификации выпускаемых изделий следующим образом. На каждом месте работы или в быту потребители сталкиваются с выбором качественных предметов из совокупности однородных предметов. Например, при покупке машины, одежды или фруктов мы можем просмотреть вначале целый ряд примерно однородных предметов, прежде чем остановим свой выбор одном из них. Или возьмем другой пример, относящийся к производству: при выпуска изделий его качества рассматривается специальными комиссиями, которые оценивают производственные достижения и качество работы отдельных работников и целых коллективов, затем ранжируются по степеням, качеству работы однородных предприятий и работников. Отсюда видно, что каждый член комиссии выставляет определенную оценку, основываясь на объективных признаках, а также своем профессиональном опыте и интуиции.

Отсюда вытекает вопрос: нельзя ли, анализируя трудовую и качественную деятельность каждого производства товаров, автоматизировать вышеизложенные процессы, используя современные новые информационные технологии? Если этот вопрос реализуется, то не будет нужды создавать комиссии для обработки информации выпускаемых изделий ручным способом, так как у нас будет формализованный способ решения задачи классификации параметров, которые позволяет качества выпускаемых изделий предприятия.

Классификация выпускаемых изделий, на основе удовлетворенности спроса потребителей, т. е. учитывая совокупность качеств в условиях функционирования новые информационные технологии предприятий торговли — более сложная проблема. Однако успешное функционирование производства во многом зависит от качественного уровня товаров. Главным критерием распределения выпускаемых товаров по спросам потребителей должна быть только труд — его количество и качество. Однако, в практических условиях не всегда бывает так. Возникает различного рода уравниловка, факты начисления зарплаты по существу лишь за явку на работу, а не за ее реальные результаты, выдача незаслуженных премий и т. д. Устранение таких вредных явлений в обществе во многом зависит от формирования социальных качеств работников производство и управляющего персонала предприятий. По этому поводу надо отметить следующие факторы: для производства качественных изделий необходимо всегда и повсеместно обеспечивать справедливую и объективную оценку трудового вклада каждого работающего. Надо всемерно поощрять добросовестных работников [1,2], не оставлять лодырям и бракоделам никаких лазеек для хорошей жизни при никудышной работе.

Исходя из этого, в настоящее время производства ощущает подобрать в таких математических моделей и технологии, которые обладают высокими уровнями качеств выпускаемых изделий.

Постановка задачи классификации качеств выпускаемых изделий на основе их степени спроса и других качественных и количественных признаков осуществляется впервые. Реализацию этой задачи можно использовать как методику руководителями при системе управлении и поддержки принятия решений для самоорганизации социально-экономических систем предприятия торговли. Теперь сформулируем постановку задачи на языке математического аппарата.

Пусть 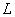 — статистическое пространство. Элементами  является множество сырье подлежащих в производстве. Предположим, что каждый товаров характеризуется набором количественных и качественных признаков 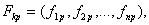 которые описывают 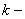го товара как 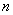-мерные точки в , -где .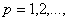

Задача классификации товаров по их качествам производится разбиением 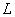на классы [3], так что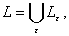 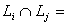 Ø или 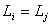 и отнести 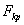-го товара к одному из классов 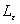. Пространство  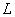является однородным, если выполняется условие [4,5],  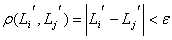где 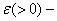заданное число;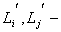выборочные среднее значение соответственно, класса  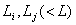и вычисляется: 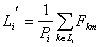, 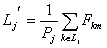. Класс 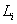является однородным, если выполняется условие:  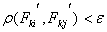(1) где 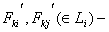выборочное среднее значение  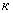и 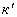 товара вычисляется соответственно:

, .

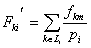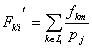Теорема. Рассмотрим случайную величину, 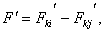 т. е. разность средних двух выборок  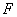имеет выборочное распределение со средним  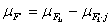и дисперсией 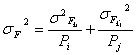(2). Если  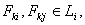то обозначая 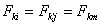и по (2) получаем:  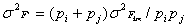(3)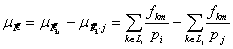 (4). Тогда выборочные оценки дисперсий в классе  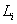равны: 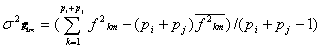(5).

Используя, (3) и (5) получим меру рассеяния элементов в пространстве 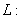 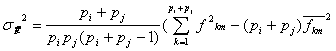 (6). Используя метод максимального правдоподобия, определим плотность вероятности нормального распределения качества признаков товара в классе  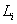и 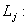 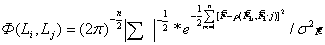 (7). Из (7):  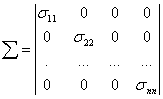учитывая, (1) получим  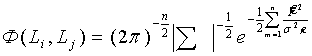(8). Из (8) вычислим  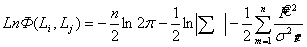отсюда следует:  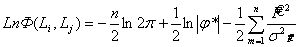(9) где  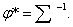Из (9) видно, что если  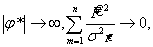то 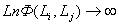. Функция (7) имеет максимальное значение, если выражение  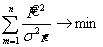(10).

Выражение из (10) заменим их значениями, приведенными в (4) и (6): 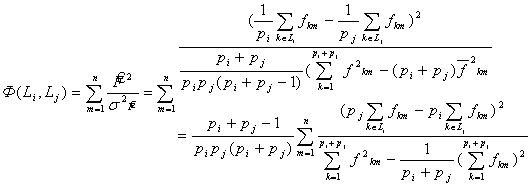 (11)

где 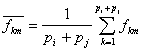 должна достигаться в минимальном значении при  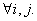Однородность класса  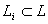достигается при  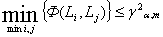(12) где 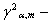пороговое значение, по уровню значимост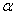и и 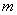степенями свободы.

Литература:

1.         Анициферова В. И., Зольников В. К. Анализ подготовки специалистов по радиоэлектронике для научно-производственных и коммерческих структур в современных условиях.Моделирование систем и процессов. 2009. № 3–4.С.5–12.

2.         БеляеваТ. П., Зольников В. К., Чубур К. А. Экспертно-мониторинговый анализ на этапе выработки и поддержки принятия управленческих решений. Моделирование систем и процессов. 2012. № 1. С.22–27.

3.         Бибиков Ю. Н. Курс обыкновенных дифференциальных уравнений: учеб. для вузов. — М.: Лань, 2011. — 304 с.

4.         Гладков Л. А., Курейчик В. В., Курейчик В. М. Генетические алгоритмы: учеб. для вузов. — М.: Физматлит, 2010. — 368 с.

5.         Зольников В. К., Манучарян Л. А. Валидация извлеченной информации на основе онтологического описания. Моделирование систем и процессов. 2012. № 3.С.28–30.

6.         Abdullaev U. A. Modeling of the development of trade-based enterprise application software package Maple.// 1^st International Scientific Conference, European Applied Sciences: modern approaches in scientific researches, Stuttgart, Germany December 17–19, 2012. P. 139–142.