В литературе освещен вопрос о существования и построения асимптотических решений систем линейных дифференциальных уравнений первого и второго порядков [1;3]. Что же касается систем уравнений высших порядков, то они изучены мало. Сведение таких систем к системам первого порядка повышает степень характеристического уравнения. Кроме того, такие сведение приводит к очень громоздким вычислениям.
Системы линейных дифференциальных уравнений высших порядка изучены в работе [4].
В данной работе исследуются системы нелинейных дифференциальных уравнений порядка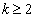 
вида
(1)
где х, f — n- мерный векторы, из них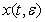 
искомый, A(τ,ε) — n- мерный квадратный матрицы, ε>0малые параметр, 
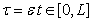медленные время, 
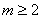натуральный, L>0 данный число, A(τ,ε) — квадратная матрица n-го порядка, допускаются разложения
(2)
Известно, что структура формальных, в смысле [1,2]частных решений системы (1) тесно связана с поведением корней так называемого характеристического уравнения
det [A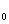
(τ)-λE]=0, (3)
где E — единичная матрица.
В настоящей работе рассматривается вопрос построения решения системы (1) при наличии нулевого корня уравнение (3), т. е. так называемый критический случай [5]. Этот случай, для системы вида (1) в литературе не рассматривались. Поэтому несомненно представляет определенный интерес исследование систем вида (1), к которым приводятся некоторые задачи физики и техники.
В дальнейшем будем считать, что выполняются условия:
1. Матрицы на отрезке [0,L] неограниченное число раз дифференцируемы;
2. ƒ(τ,x,ε) вектор в области , где P(τ,x) — некоторая область пространства переменных τ, x неограниченно дифференцируемых;
3. При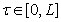 
корни уравнение (3) удовлетворяют условия
(4)
4. , (5)
где (см. [3]), для функции дадим пояснение несколько позже.
Справедлива теорема.
Теорема 1. Если для системы дифференциальных уравнений (1) выполняются условия 1–4, то уравнения (1) имеет формальные частные решение вида
(6)
Доказательства. Подставляя (6) в (1), раскладывая векторƒ(τ,u(τ,ε),o) в ряд Тейлора в окрестности точки ив полученном разложении собираем члены с одинаковыми степенями ε. Итак, имеет соотношение
(7)
где элементы матрицы и компоненты вектора вычисляются в точке ,авектор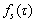
(s=2,3,…) выражаются определённым образом через .
Приравнивая коэффициенты при, одинаковых степенях ε в равенства (7), получим рекуррентные уравнения для определения неизвестных элементов ряда (6).
,(8)
,(9)
,(10)
..................…………………………………………….
,(11)
где
Покажем разрешимость этих уравнений, из уравнения (8) согласно [6], находим
,(12)
где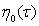 
- произвольные, отличные от нуля , функции, которые определяем на следующем иначе.
Уравнение (9), с учетом (12) имеет вид
(13)
Для разрешимости уравнения (13) необходимо и достаточно для выполнения условия разрешимости вида
(14)
Отсюда имеем
(15)
Таким образом, получаем нелинейное алгебраическое уравнение относительно неизвестных функции .
Предположим, что для уравнения (15) выполняются все условия теоремы о неявной функции [7] и определим . Так как условие разрешимости для уравнения (13)имеет место, то находим
,(16)
где
,
— неизвестная функция, которая определяется наследующем шаге, а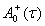 
— обобщенно-обратная матрица к матрице , имеющая вид
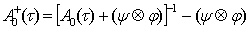, (17)
здесь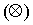 
- знак тензорного произведения векторов 
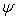и 
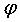из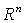 
.
Учитывая (16), уравнение (10)запишем так
(18)
Согласно условию разрешимости вида (14), получаем алгебраическое уравнение для определения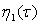 
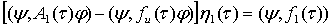. (19)
Отсюда с учетом (5) имеем
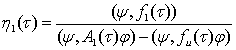(20)
Условие (19) для уравнения (18) имеет место, то из уравнения (18) находим
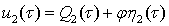, (21)
где
,
а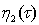 
, как предыдущая неизвестная функция, определяется на следующем шаге.
Продолжая этот процесс, из (11) получаем уравнения для определения элементов ряда (6), т. е.
, (22)
где
.
Пусть для уравнения (22) выполняется условие вида (14)
. (23)
Отсюда получим
. (24)
Из уравнения (24) определим неизвестная функции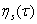 
:
. (25)
Так как для уравнения (22) условия (23) выполняются, то находим
, (26)
где
,
а 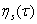неизвестная функция, определяется на следующем шаге.
Описанная здесь схема решения показывает, как можно найти элементы формального ряда (6), т. е. векторы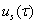 
с любым номером 
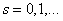. Теорема 1 доказана.
В заключение рассматриваемого вопроса сформулируем теорему, указывающую на асимптотический характер построенного решения (6).
Теорема 2. Пуст для системы дифференциальных уравнений(1) выполняются условия теоремы 1 и вектор-функция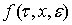 
удовлетворяет условия Липшица с постоянной l:
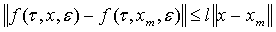(27)
а также
, 
, 
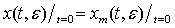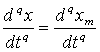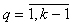, (28)
где 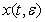— точное, 
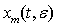— m- приближенное решение системы (1). Тогда для произвольногоL>0 существует постоянная c>0, независящая от ε и такая, что 
, 
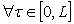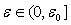имеют место неравенства
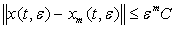, (29)
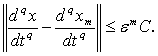(30)
Литература:
1. Боголюбов Н. И., Митропольский Ю. А. Асимптотические методы в теории нелинейных колебаний. — М.: Наука, 1974, — 504 с.
2. Фещенко С. Ф., Шкиль Н. И., Ныколенко Л. Д. Асимптотические методы в теории линейных дифференциальных уравнений. — К: Наукова думка, 1966, — 252 с.
3. Сотниченко Н. А., Фешенко С. Ф. Асимптотическое интегрирование дифференциальных уравнений. — К: 1980, — 48 с. — /Препринт/ А. Н. УCCР, Ин-т математики; 80. 3/.
4. Шкиль Н. И., Кушнир В. А. Об асимптотическом решении систем линейных дифференциальных уравнений высших порядков в случае кратных корней характеристического уравнения. — В сб.: Суммирование расходящихся рядов и дифференциальные уравнения с малым параметром. К.: КГПН, 1985, с. 112–118.
5. Васильева А. Б., Бутузов В. Ф. Сингулярной возмущение уравнения в критических случаях. — Изд. МГУ, 1978. — 107 с.
6. Алишев А. Г. Решение нелинейных дифференциальных уравнений. Дробного ранга. ДАН. УССР. Сер А, № 6, 1982, с. 6–9.
7. Фихтенгольц Г. М. Основы математического анализа. — М: Наука, т.1. 1968, –464 с.
