Система выбора поставщиков перерабатывающего предприятия в условиях неопределенности

В условиях изобилия в стране количество поставщиков производственных ресурсов резко увеличилось. Перерабатывающие предприятия, зависящие во многом от поставщиков, стараются отыскать для себя наиболее оптимальный вариант, который полностью будет удовлетворять всем требованиям, как заказчика, так и исполнителя. С этой целью была разработана и предложена методология выбора поставщиков по качественному параметру с применением лингвистических переменных, подсистемы логического вывода в теории нечетких множеств. Данная методология позволяет пользователю принять адекватное решение о выборе необходимого исполнителя заказа по установленным параметрам в кротчайшие сроки.

Введение

Перерабатывающие предприятия во многом зависят от качества поставляемой продукции. При качественном и не дорогом сырье продукция, выпускаемая предприятием, будет во многом определять такие экономические показатели предприятия, как выручка, прибыль и рентабельность. Поэтому перед данными предприятиями особо остро встает вопрос выбора наиболее приемлемого поставщика ресурсов. Достаточно сложно количественно оценить и ранжировать поставщиков ресурсов по таким параметрам, как качество, цена, условия оплаты, кредитоспособность, дополнительные услуги, сроки и способ поставок, комплектность поставок, надежность поставок и т. д. В этом случае лицу, принимающему решение, гораздо удобнее оперировать не с количественными, а с качественными оценками. В реальных условиях задача состоит в выборе из множества поставщиков, оцениваемых по множеству параметров.

Выбор наиболее привлекательных поставщиков по качественному параметру

К примеру, будем считать, что база данных о поставщиках содержит информацию, систематизированную в таблице 1.

Таблица 1

База данных о поставщиках

Эти данные являются основой для построения базы знаний экспертной системы, основанной на использовании правил формата «Если-То». Будем использовать три вербальные оценки, характеризующие привлекательность поставщиков: отлично, хорошо и удовлетворительно. Пример написания правила формата «Если-То» представлен ниже:

Правило 1. Если: Цена поставок должна быть низкая

То: Поставщик 1 подходит удовлетворительно

Поставщик 2 подходит отлично

Поставщик 3 подходит удовлетворительно

Поставщик 4 подходит хорошо

После написания правил (п. 3.2.), имеется набор правил с неформализованными условиями и выводами, составляющими базу знаний и обеспечивающими работу подсистемы логического вывода [1].

Лингвистические переменные в теории нечетких множеств

Лингвистическая переменная отличается от числовой переменной тем, что ее значениями являются не числа, а слова или предложения в естественном или формальном языке. Поскольку слова в общем менее точны, чем числа, понятие лингвистической переменной дает возможность приближенно описывать явления, которые настолько сложны, что не поддаются описанию в общепринятых количественных терминах. Поэтому основой метода нечетких множествах является применение лингвистических переменных, их обработка для дальнейшей оценки поставщиков по качественному параметру.

В частности, нечеткое множество, представляющее собой ограничение, связанное со значениями лингвистической переменной, можно рассматривать как совокупную характеристику различных подклассов элементов универсального множества. В этом смысле роль нечетких множеств аналогична той роли, которую играют слова и предложения в естественном языке.

Важным аспектом понятия лингвистической переменной является то, что эта переменная более высокого порядка, чем нечеткая переменная, в том смысле, что значениями лингвистической переменной являются нечеткие переменные. Например, значениями лингвистической переменной Возраст могут быть: молодой, немолодой, старый, очень старый, немолодой и не старый, вполне старый и т. п. Каждое из этих значений является названием нечеткой переменной.

В нашем случае после написания правил для оценки поставщиков используем лингвистическую переменную X=привлекательность, определенную на универсальном подмножестве, представляющем интервал [0,1]. Терм-множество Х записывается в виде:

Т(Х) = {удовлетворительная, хорошая, отличная}

Функции совместимости значений удовлетворительная, хорошая, отличная упрощенно записываются как наборы упорядоченных пар:

М(удовлетворительная)={(0;1),(0,1;1),(0,2;0,85),(0,3;0,3),(0,4;0,1)}

М(хорошая)={(0,3;0,25),(0,4;0,7),(0,5;1),(0,6;0,7),(0,7;0,25)}

М(отличная)={(0,6;0,1),(0,7;0,3),(0,8;0,85),(0,9;1),(1;1)}

Для функций принадлежности термов используется либо треугольная форма, либо экспоненциальная. В данном случае используем экспоненциальные функции. В функциях совместимости значений первое число из набора упорядоченных пар является нечетким числом, второе — уровень значимости нечеткого числа [1].

Сумму весовых коэффициентов будем считать равным значением для каждого параметра:

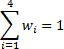
При выборе мы стремимся к тому, чтобы оценка привлекательности была как можно ближе к 1. Эту цель можно изобразить с помощью нечеткого множества число, близкое к 1, которое определим следующим образом:

G= {(0,5;0,1),(0,6;0,2),(0,7;0,3),(0,8;0,6),(0,9;0,9),(1,1)}

Далее берем разницу уровней значимости нечетких чисел между числом, близким к 1, и поставщиками ресурсов. Разницу обозначим соответственно d. По критерию минимального расстояния Хемминга выбираем поставщика [1].

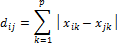
Считаем наиболее привлекательного того поставщика, у которого разница значимостей нечетких чисел d будет минимальной.

Заключение

На основании анализа проблемы выполнен проект выбора поставщиков в условиях неопределенности с применением теории нечетких множеств. В основе данной методологии явную роль при выборе поставщиков играют лингвистические переменные. Благодаря данному параметру и обобщенному расстоянию Хемминга удается ранжировать и выбирать поставщиков по качественному параметру наиболее эффективным способом.

Чтобы учитывать возможные объемы поставляемой продукции у поставщиков после качественной оценки есть возможность произвести количественную оценку с помощью методов кластерного анализа.

Следует развивать и автоматизировать данное направление деятельности предприятия с целью максимизации прибыли от качественного решения, и минимизации сбоев в работе предприятия, которые могут быть вызваны принятием не корректного решения.

Литература:

1.    Птускин А. С. Нечеткие модели и методы в менеджменте. Изд-во МГТУ им. Баумана, 2008, 216 c.