В статье представлены результаты вычислительного эксперимента, анализа и количественной оценки минимизации времени отклика многомерных интервально-логических регуляторов.
Ключевые слова: многомерный интервально-логический регулятор, оценка минимизации времени отклика.
Многомерные интервально-логические регуляторы (МИЛР) являются альтернативной ступенью развития нечётких и дискретно-логических регуляторов, где основной упор делается на повышение быстродействия систем автоматического регулирования и компенсацию взаимного влияния контуров регулирования. Отличительной особенностью структуры МИЛР является отсутствие в ней элементов обработки системы продукционных правил [1, с. 30].
Концепция построения МИЛР позволяет организовать логический вывод в виде системы консеквентов продукционных правил, что, по сути, представляет собой массив значений управляющих воздействий на многомерный объект управления, и механизма формирования идентификационных (ID) номеров продукционных правил, предназначенного для определения комбинации значений управляющих воздействий в момент t [2, c. 30].
Выполним вычислительный эксперимент и количественную оценку минимизации времени отклика многомерной системы регулирования на базе МИЛР с 2 входными параметрамиX и 2 выходными параметрами Z, схема которого представлена на рис. 1, где И1, И2 — интервализаторы, а Д1 и Д2 –деинтервализаторы МИЛР; Nmin, Nтек и Nmax — минимальный, текущий и максимальный ID-номер продукционного правила в базе данных блока логического вывода (БЛВ) соответственно; # — элемент ID-номера продукционного правила, формируемого из номеров термов T(X1), T(X2), T(Z1) и T(Z2).
Для осуществления сравнительного анализа возьмем многомерный дискретно- логический регулятор (ДЛР) с тем же числом параметров, но без ANY-TIME алгоритма фаззификации.
Распределение максимального числа продукционных правил R и операций сравнения L ДЛР и МИЛР в зависимости от суммарного числа термов K приведено в табл. 1 и 2 соответственно, где
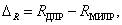
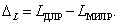
Процент сокращения максимального числа продукционных правил МИЛР ΔR рассчитывается согласно выражению
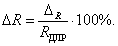
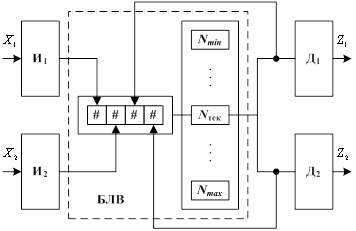
Рис. 1. Блок-схема МИЛР с 2 входными параметрамиX и 2 выходными параметрами Z
Таблица 1
Распределение максимального числа продукционных правил R ДЛР и МИЛР
|
Количество термов K непрерывных величин |
Максимальное число продукционных правил R |
ΔR, % |
|||||
|
X1 |
X2 |
Z1 |
Z2 |
ДЛР |
МИЛР |
ΔR |
|
|
3 |
3 |
3 |
3 |
256 |
82 |
174 |
67,97 |
|
4 |
4 |
4 |
4 |
625 |
257 |
368 |
58,88 |
|
5 |
5 |
5 |
5 |
1296 |
626 |
670 |
51,70 |
|
6 |
6 |
6 |
6 |
2401 |
1297 |
1104 |
45,98 |
|
7 |
7 |
7 |
7 |
4096 |
2402 |
1694 |
41,36 |
|
8 |
8 |
8 |
8 |
6561 |
4097 |
2464 |
37,56 |
|
9 |
9 |
9 |
9 |
10000 |
6562 |
3438 |
34,38 |
Следует отметить, что максимальное число операций сравнения L ДЛР принято равным максимальному числу продукционных правил R. Это следует из того, что в логических регуляторах максимальное число операций сравнения напрямую зависит от числа правил, каждое из которых может содержать несколько операций сравнения.
В табл. 2 процент сокращения максимального числа операций сравнения ∆L МИЛР рассчитан, согласно выражению
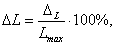
где максимальное число операций сравнения Lmax = LДЛР.
Таблица 2
Распределение максимального числа операций сравнения L ДЛР и МИЛР
|
Количество термов K непрерывных величин |
Максимальное число операций сравнения L |
ΔL, % |
|||||
|
X1 |
X2 |
Z1 |
Z2 |
ДЛР |
МИЛР |
ΔL |
|
|
3 |
3 |
3 |
3 |
256 |
16 |
240 |
93,75 |
|
4 |
4 |
4 |
4 |
625 |
20 |
605 |
96,80 |
|
5 |
5 |
5 |
5 |
1296 |
24 |
1272 |
98,15 |
|
6 |
6 |
6 |
6 |
2401 |
28 |
2373 |
98,83 |
|
7 |
7 |
7 |
7 |
4096 |
32 |
4064 |
99,22 |
|
8 |
8 |
8 |
8 |
6561 |
36 |
6525 |
99,45 |
Из табл. 2 следует, что
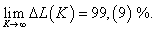
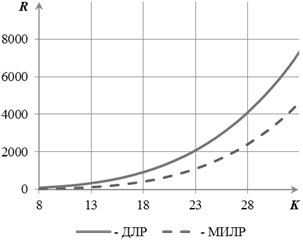
На рис. 2, а) изображён график зависимости максимального числа продукционных правил R ДЛР и МИЛР от суммарного числа термов K, из которого следует, что при K, равном 32, разница между максимальным числом правил ДЛР и МИЛР составляет 2464 правила, а сокращение максимального числа правил ∆R МИЛР составляет 37,56 %.
а) б)
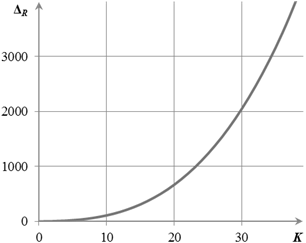
Рис. 2. Графики зависимости параметров R ДЛР и МИЛР (а) и ΔR (б) от суммарного числа термов K
График зависимости ΔR от общего числа термов K непрерывных физических величин многомерной системы управления представлен на рис. 2, б), из которого следует, что
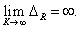
На рис. 3, а) представлен график зависимости максимального числа операций сравнения L ДЛР и МИЛР от суммарного числа термов K, из которого следует, что при K, равном 8, разница между максимальным числом операций сравнения ДЛР и МИЛР составляет 69 операций, сокращение максимального числа операций сравнения ∆L МИЛР составляет 85,19 %.
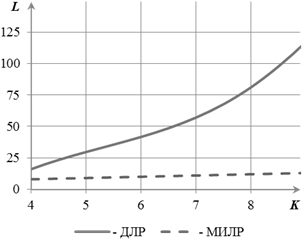
График зависимости параметра ΔL от суммарного числа термов K непрерывных физических величин многомерной системы управления представлен на рис. 3, б).
а) б)
Рис. 3. Графики зависимости параметров L ДЛР и МИЛР (а) и ΔL (б) от суммарного числа термов K
Рассмотрим пример работы STEP-TIME алгоритма интервализации (фаззификации) непрерывных величин в МИЛР.
В табл. 3 представлено случайное распределение значений параметра минимизации ∆F МИЛР с 3 входными параметрами X в течение 12 циклов сканирования, где
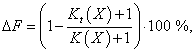
где Kt(X) — номер терма величины X, равного логической единице в момент времени t.
Средний процент увеличения быстродействия процедуры интервализации (фаззификации) ∆F МИЛР за 12 циклов составляет 39,17 %, 21,11 % и 45,71 % по каждому из X.
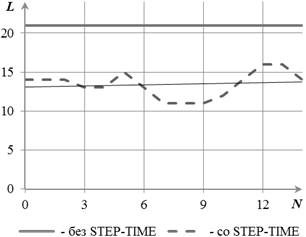
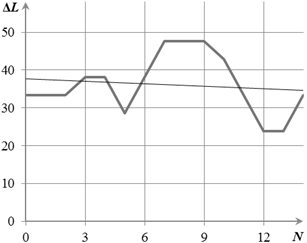
На рис. 4, а) и б) приведен пример распределения параметров L и Δ L МИЛР в течение 12 циклов сканирования в результате использования STEP-TIME алгоритма.
Таблица 3
Распределение значений параметра ∆F МИЛР в течение 12 циклов сканирования
|
X1 |
X2 |
X3 |
ИМИЛР |
||||||||
|
Kt |
K |
∆F, % |
Kt |
K |
∆F, % |
Kt |
K |
∆F, % |
Lt |
L |
∆L, % |
|
5 |
7 |
25,00 |
5 |
5 |
0,00 |
1 |
6 |
71,43 |
14 |
21 |
33,33 |
|
5 |
7 |
25,00 |
5 |
5 |
0,00 |
1 |
6 |
71,43 |
14 |
21 |
33,33 |
|
6 |
7 |
12,50 |
4 |
5 |
16,67 |
1 |
6 |
71,43 |
14 |
21 |
33,33 |
|
5 |
7 |
25,00 |
4 |
5 |
16,67 |
1 |
6 |
71,43 |
13 |
21 |
38,10 |
|
4 |
7 |
37,50 |
4 |
5 |
16,67 |
2 |
6 |
57,14 |
13 |
21 |
38,10 |
|
4 |
7 |
37,50 |
5 |
5 |
0,00 |
3 |
6 |
42,86 |
15 |
21 |
28,57 |
|
3 |
7 |
50,00 |
4 |
5 |
16,67 |
3 |
6 |
42,86 |
13 |
21 |
38,10 |
|
2 |
7 |
62,50 |
3 |
5 |
33,33 |
3 |
6 |
42,86 |
11 |
21 |
47,62 |
|
2 |
7 |
62,50 |
3 |
5 |
33,33 |
3 |
6 |
42,86 |
11 |
21 |
47,62 |
|
2 |
7 |
62,50 |
3 |
5 |
33,33 |
3 |
6 |
42,86 |
11 |
21 |
47,62 |
|
3 |
7 |
50,00 |
3 |
5 |
33,33 |
3 |
6 |
42,86 |
12 |
21 |
42,86 |
|
3 |
7 |
50,00 |
4 |
5 |
16,67 |
4 |
6 |
28,57 |
14 |
21 |
33,33 |
а) б)
Рис. 4. Пример распределения параметров L и Δ L МИЛР в течение 12 циклов
Литература:
1. Антипин А. Ф. Об одном способе анализа структуры многомерного четкого логического регулятора // Прикладная информатика. 2012. № 5. С. 30–36.
2. Антипин А. Ф. Особенности программной реализации многомерных логических регуляторов с переменными в виде совокупности аргументов двузначной логики // Автоматизация и современные технологии. 2014. № 2. С. 30–36.







