В данной статье рассматривается роль упражнений на готовых чертежах в обучении решению геометрических задач. Приводится система упражнений, по теме «Признаки равенства треугольников», направленная на формирование действий, адекватных изучению понятий и теорем и способствующая обучению учащихся приемам работы с геометрическим чертежом.
Ключевые слова:упражнения на готовых чертежах, работа с чертежом, решение геометрической задачи.
Известно, что при обучении геометрии огромное значение имеет умение решать задачи, требующее установление соотношений между данными и искомыми. Часто связь между данными и искомыми задачи раскрывается не непосредственно, а в результате использования других данных, с помощью применения основных понятий и теорем.
При решении подобного рода задач проявляется уровень математического развития учащихся. Так как для того, чтобы ее решить необходимо умение работать с геометрическим чертежом, умение рассматривать и выделять на чертеже фигуры, нужные для решения. Анализируя условие задачи, учащиеся могут выделить нужные связи и отношения на чертеже. Для этого требуются хорошие знания основных понятий и теорем, умение анализировать, преобразовывать, переформулировать задачу, вести рассуждения, вычленять проблему, то есть достаточно высокая логическая подготовка.
Обучению учащихся приемам работы с чертежом способствуют упражнения на готовых чертежах, повышающиеся эффективность урока и положительно воздействующие на активизацию мыслительной деятельности учащихся.
Рассмотрим систему упражнений на готовых чертежах по теме «Признаки равенства треугольников», которые предлагаются учащимся, после изучения всех признаков равенства треугольников.
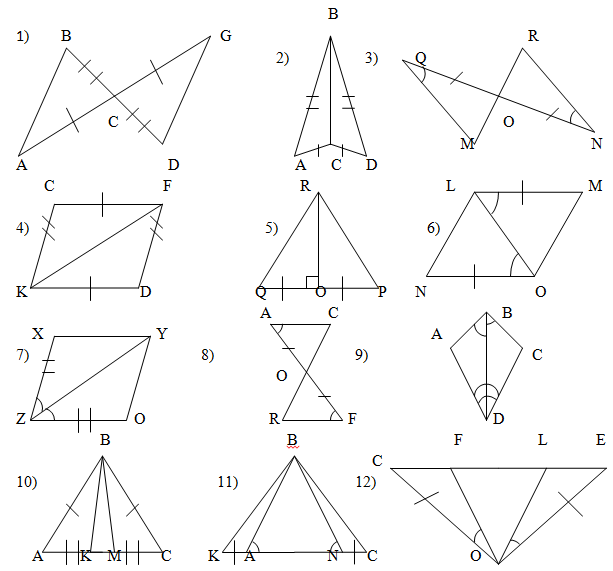
1. Найдите равные треугольники, пользуясь первым признаком равенства треугольников (рис.1).
2. Пользуясь вторым признаком равенства треугольников, выберите равные треугольники (рис. 2, а-г).
3. Пользуясь третьим признаком равенства треугольников, выберите равные треугольники (рис. 3, а-г).
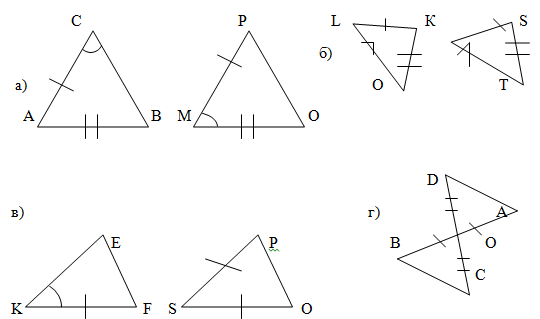
Рис. 1.
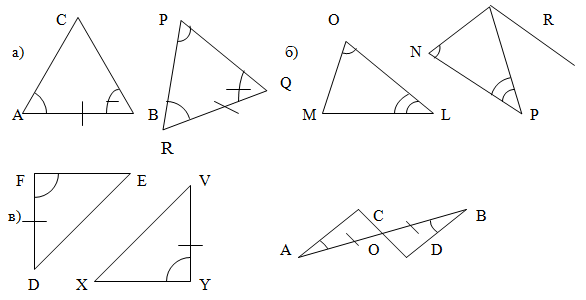
Рис. 2.
4. Можно ли утверждать, что:
а) 
(рис.1, а); б) 
(рис.1, б);
в) ЕК=ОР (рис. 1, в); г) DE=VX (рис.2, в);
д)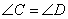 
(рис.2, г); е) 
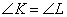(рис.3, а);
ж) AB=A1B1 (рис.3, б); з)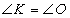 
(рис.3, в)?
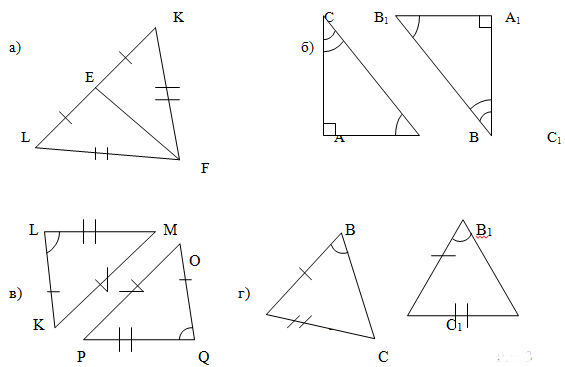
Рис. 3.
5. Укажите равные треугольники, пользуясь признаками равенства треугольников (рис. 4).
После выполнения упражнений 1–3 на готовых чертежах, учитель может легко диагностировать уровень сформированности учебных действий у учащихся. Если они не выбрали случай г в первом упражнении, случаи а и г во втором и случаи а и в в третьем, то это свидетельствует о не сформированности действия распознавания ситуаций, удовлетворяющих соответственно первому, второму и третьему признаку равенства треугольников.
Если при выполнении упражнения 4 учащиеся допускают ошибки, то это свидетельствует о том, что не сформировано действие преобразования заключения теоремы и действие осмысления связей между элементами задачи.
В результате выполнения упражнения 5 учащиеся распознают равные треугольники, применяя самостоятельно один из необходимых признаков, оперируют свойствами равнобедренного треугольника, свойствами смежных и вертикальных углов.
Верное выполнение учащимися всех заданий свидетельствует о сформированности у них умения применять знания в новой, видоизменной ситуации, используя общелогические и эвристические действия, приемы.
Упражнения, предложенные учащимся, направленны на наглядное восприятие признаков равенства треугольников, формирование целостной системы знаний и умений по данной теме геометрии. Они способствуют своевременному выявлению отклонения в сформированности действий, адекватных изучению понятий и теорем, и внесению корректив и изменений в процесс обучения.
Практика обучения геометрии, опыт учителей свидетельствует о том, что целенаправленная работа по формированию и развитию умений решать геометрические задачи способствует усвоению учащимися теоретических знаний, применению их к решению разного типа задач. Упражнения на готовых чертежах позволяют совершенствовать процесс формирования умения решать геометрические задачи, оказывают положительное влияние на развитие пространственного воображения и творческого мышления, необходимого для решения стереометрических задач, усиливают прикладную направленность преподавания планиметрии. У учащихся формируются умения анализировать задачную ситуацию, заданную чертежом, обобщения и конкретизации чертежа. Они владеют методами и приемами исследования геометрической ситуации, геометрического чертежа, анализируют условие задачи и соотносят его с чертежом, выбирают наиболее эффективный способ решения задачи.
Литература:
1. Новичкова Т. Ю., Гудкова В. С., Ячинова С. Н. Современные средства оценивания результатов обучения // Молодой ученый. 2014. № 6 (65). С. 740–742.
2. Новичкова Т. Ю., Хвастунова Е. М., Ячинова С. Н. Критериальные задания как фактор совершенствования процесса обучения математике // Вестник магистратуры. 2014. № 6–1 (33). С. 125–127.
3. Саранцев Г. И. Методика обучения математике в средней школе: Учеб. пособ. для студентов мат. спец. пед. вузов и университетов. — М.: Просвещение, 2002. — 224с.
4. Титова Е. И., Чапрасова А. В., Ячинова С. Н. Формирование умений работы с чертежом в процессе решения геометрических задач // Современные проблемы науки и образования. 2014. № 2. С.269.
5. Шатилова А. В. Обучение школьников составлению геометрических задач по готовым чертежам: автореф. дисс. … канд. пед. наук. — Саранск, 1997. — 16 с.
6. Ячинова С. Н. Цели обучения как средство управления учебной деятельностью на уроке математики: дисс. … канд. пед. наук. — Пенза, 2003. — 165 с.
