Ключевые слова: распознавание образов без учителя, техническая диагностика, таксономия, классификация.
Введение. Методы кластеризации являются одними из наиболее востребованных при решении задач анализа многомерных данных. Группировка объектов по схожести их свойств упрощает решение многих практических задач. В таких задачах решающую роль играют возможности кластеризации для формализации значений признаков, определения степени сходства объектов.
Теория распознавания образов является основным методологическим комплексом для анализа данных об объектах исследования.
В теории распознавания образов выделяют два основных подхода: распознавание образов (классификация) с учителем и без учителя (самообучение). Группировка объектов по похожести их свойств («самообучение», «автоматическая классификация», «кластеризация», «таксономия») упрощает решение многих практических задач анализа данных. Так, если объекты описаны свойствами, которые влияют на общую оценку их качества, то в одну группу (таксон, класс, кластер) будут собраны объекты, обладающие приблизительно одинаковым качеством. И вместо того, чтобы хранить в памяти ЭВМ данные обо всех объектах, достаточно сохранить описание типичного представителя каждого таксона (прецедента), перечислить номера объектов, входящих в данный таксон, и указать максимальное отклонение каждого свойства от его среднего значения для данного таксона. Этой информации обычно бывает достаточно для дальнейшего анализа изучаемого множества объектов [1].
Несмотря на существование множества алгоритмов группировки данных, при реализации большинства из них возникают некоторые трудности. При решении практических задач как правило выбирается критерий качества (в один кластер должны собираться объекты, похожие по своим характеристикам), но не указывается, для какой конкретной цели эта группировка делается. Помимо того, что кластеры должны объединять похожие элементы, количество кластеров еще должно быть минимальным и достаточным для принятия правильных решений на следующем более высоком уровне системы. Окончательный вариант разбиения исследуемых объектов на группы решающим образом зависит от выбора метрики или меры близости объектов. В каждой конкретной задаче этот выбор производится по-своему, с учетом главных целей исследования, физической и статистической природы используемой информации и т. п. Если гипотеза о типе группировок неверна, то нацеленность алгоритмов кластерного анализа на определенную структуру группировок может приводить к неоптимальным или даже неправильным результатам.
Общий вид алгоритма классификации. Применение методов распознавания образов предполагает существование исходных эмпирических данных об изучаемом множестве объектов в системе их признаков. В общем виде они могут быть представлены в виде матрицы W размерностью N n, где N — количество объектов (экспериментальных точек), а n — количество признаков (свойств, характеристик и факторов), характеризующих данное множество объектов.
В таком случае каждый объект геометрически можно представить в виде точки в n-мерном пространстве признаков, а под классом будем понимать множество объектов, близких между собой в некотором смысле. «Мера близости» между объектами одного класса при этом больше, чем между объектами разных классов. Суть понятия «мера близости» основана на «гипотезе компактности» и заключается в следующем: объекты одного и того же класса в пространстве признаков образуют геометрически близкие точки, т. е. компактные «сгустки». Большинство подходов в распознавании образов основано именно на этой гипотезе.
В настоящее время существует ряд алгоритмов и программных комплексов, позволяющих решать разнообразные типичные задачи классификации. В данном случае рассматривается следующая задача: имеется набор (база) данных, содержащий сведения о качестве технических изделиях [2]. Необходимо отделить изделия, которые могут быть отнесены к группе высококачественных, от среднего и более низкого качества.
Задача классификации в общем виде. Пусть имеется совокупность объектов О1, О2,..,Оn, заданных в виде матрицы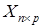 
(p — количество входных параметров (признаков), n — объем выборки изделий). Требуется разбить их на группы объектов, в каком-то смысле близких между собой. Таким образом, задача классификации заключается в разбиении пространства признаков на непересекающиеся области.
Далее рассмотрим некоторые алгоритмы, предлагаемые (разработанные) для группировки данных в случае, когда исходное число классов неизвестно.
Алгоритм кристаллизации. Пусть имеется выборка наблюдений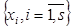 
многомерной переменной 
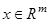, где m — размерность переменной x, 
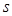— объем выборки. Необходимо выделить из имеющейся выборки наблюдений классы. Количество классов неизвестно. На Рис.1 представлен возможный вариант расположения точек в пространстве для случая m=2.
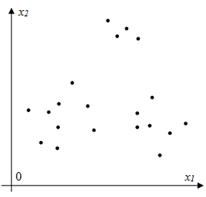
Рис.1. Взаимное расположение точек выборки в пространстве состояний
Предложен следующий алгоритм классификации.
1. Найти расстояния между всеми точками выборки наблюдений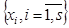 
. Многомерное расстояние 
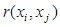между двумя многомерными точками 
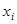и 
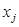вычисляется как
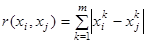. (1)
При этом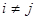 
, 
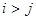. Таким образом, формируется выборка расстояний между точками, объем которой равен 
.
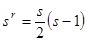2. Задать расстояние δ. Расстояние δ выбирается экспериментальным путем на основании анализа расстояний r между точками выборки.
3. Из имеющейся выборки наблюдений произвольно выбрать начальную точку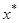 
.
4. Найти все точки, удовлетворяющие условию
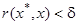. (2)
Делается предположение о том, что точки, удовлетворяющие условию (2) лежат с начальной точкой 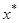в одном классе, т. е. являются ее «соседями» по классу.
5. Каждая «соседская» точка становится начальной 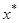и для нее повторяется пункт 4 (Рис. 2). Если новая «соседская» точка удовлетворяет условию (2) и еще не присутствует в классе, то она включается в этот класс. Процедура повторяется до тех пор, пока ни одна из точек выборки не будет удовлетворять условию (2).
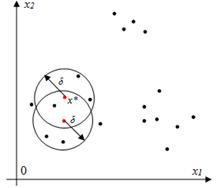
Рис. 2.
Рис. 3
6. Выделенные точки объявить классом (Рис. 3) и исключить из выборки наблюдений.
7. Повторять с пункта 2 до тех пор, пока объем выборки 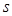не будет равен 0.
Рассмотрим результаты работы вышеописанного алгоритма. Выборка наблюдений объема s=20, в рамках вычислительного эксперимента, была сгенерирована по равномерному закону распределения в заданных границах. Расстояние δ было выбрано равным 2. Результаты работы алгоритма представлены на графике (рис. 4).
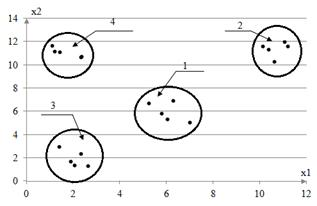
Рис. 4. Результаты работы алгоритма распознавания
На рис. 4 выделенные алгоритмом классы обведены линией. Как видно из полученных результатов, алгоритм провел классификацию безошибочно. Алгоритм выделил 4 класса, в каждом из которых по 5 точек.
Литература:
1. Загоруйко Н. Г. Прикладные методы анализа данных и знаний / Н. Г. Загоруйко. Новосибирск: Издательство ИМ СО РАН, 1999.
2. Чжан, Е. А. О компьютерной диагностике диодных матриц / Е. А. Чжан, В. И. Орлов, Н. А. Сергеева, В. В. Федосов // Системы автоматизации в образовании, науке и производстве AS’2013 // Труды IX всероссийской научно-практической конференции (с участием стран СНГ). Новокузнецк, 28–30 ноября, 2013
