Данная статья посвящена особенностям использования интеллектуальных игр на уроках математики.
Ключевые слова: игра, урок.
Опыт показывает, что игра, проведенная в дидактических целях, приносит не только хорошие результаты, но и много положительных эмоций как учащимся, так и учителю. Интеллектуальная игра — эффективная форма проведения уроков математики, поскольку наиболее прочны те знания, которые приобретались с заинтересованностью.
В этой статье предлагаю методику проведения интеллектуальной игры «Next». Продолжительность игры — два спаренных урока (в укороченном варианте — 45 мин).
Оборудование игры: секундомер, кодоскоп, переносные доски для записи заданий соответствующих конкурсов, два больших конверта, билеты с указанием номеров заданий (или бочонки из игры «Лото»).
В игре выделяются следующие роли: ведущий (учитель) проводит организационные мероприятия по подготовке к игре, готовит задания для конкурсов, объявляет задания, выслушивает ответы, оценивает каждый ответ, следит за выполнением правил игры, подводит итоги каждого конкурса, каждого тура и игры в целом; помощник ведущего (один из учеников класса или другой учитель) следит за временем, используя секундомер, выполняет указания ведущего, заполняет таблицу результатов и т. п.; капитаны команд (их избирают сами ребята) организовывают работу в команде, выделяют отвечающих и следят за выполнением правил игры. Класс делится на три команды, равные по знанию математики.
Игра проводится в два тура: в I туре играют непосредственно две команды друг с другом, а третья команда набирает очки в зависимости от ответов играющих команд. Во II туре команда-победительница меряется силами с третьей командой. А в это время проигравшая команда следит за соперниками и также набирает очки в зависимости от ответов играющих. По результатам обоих туров подсчитывают итоги игры.
В каждом туре проводятся следующие конкурсы: «Конкурс решения задач»; «Поименный конкурс»; «Таинственный конверт»; «Next».
Рассмотрим правила каждого конкурса.
Для «Конкурса решения задач» учитель заранее готовит определенное количество (10–20) заданий по теме игры. Цель этого конкурса — проверка практических умений и навыков решения математических задач.
Капитаны двух играющих команд поочередно тянут билет с номером задачи, а учитель либо вывешивает плакат с заданием на доску, либо проецирует задачу на экран с помощью кодоскопа. Все участники игры решают предложенную задачу, а отвечает команда, которая вытянула соответствующий номер. Для подготовки ответа дается, как правило, 1 мин. Так как задания в основном стандартного типа, то обсуждения в играющих командах не допускаются. Не разрешена и коллективная подготовка ответа. Определенным знаком участник команды после обдумывания показывает капитану, что он знает, как решать задачу. Капитан определяет, кто будет отвечать. За полный правильный ответ команде выставляется 1 балл. Если команда не знает ответа, или ответивший ошибся, или не дал полного ответа, то отвечает третья команда. За правильный ответ балл начисляется третьей команде. Если и эта команда не знает ответа или ответила неправильно, то отвечает команда-соперница (при этом очередность не нарушается) и ей начисляется балл (или, по усмотрению учителя, задание снимается с игры, дается на дом с разбором на последующих уроках).
Примечание. Ответивший участник команды не имеет права отвечать вторично, пока не ответили все члены команды. Команда, которая в данный момент не участвует в соревновании, может коллективно обсуждать вопросы и готовить ответы на каждый из них.
Во время проведения «Поименного конкурса» две команды поочередно задают друг другу вопросы и предлагают задачи, подготовленные самими учащимися, указывая, кто именно из участников должен отвечать. Любому участнику может быть задан в этом конкурсе только один вопрос. Команда не имеет права помогать и подсказывать отвечающему. За нарушение правил следует наказание штрафными очками. Для этого конкурса каждая команда заранее готовит по 4–6 вопросов.
На подготовку ответа также выделяется 1 мин. Если никто (и наблюдающая команда в том числе) не знает ответа, отвечает команда, задавшая вопрос. За полный ответ начисляется 1 балл (кроме случая, когда задавшая вопрос команда сама же и ответит).
Задания для конкурса «Таинственный конверт» нестандартного типа, их готовит сам учитель.
Учитель составляет по 3–6 заданий и вкладывает их в большие конверты (отдельно для каждой команды). Как правило, во время игры команды решают по три задания такого типа, вытягивая их поочередно из своих конвертов. Так как вопросы нестандартные, то участники игры имеют право обсуждать решение и коллективно готовить ответ. На подготовку ответа дается больше времени (до 3 мин), в зависимости от сложности вопроса. В этом конкурсе неважно, кто из команды будет отвечать. Если команда, которая вытянула задание, не знает ответа или ответила неверно, то отвечает сначала третья команда. Если и она не знает ответа, то или отвечает вторая команда, или задание снимается с игры. За полный ответ в этом конкурсе начисляется по 2 балла.
В целом, по усмотрению учителя, возможна и другая система баллов.
Конкурс «Next» посвящен систематизации и обобщению теоретических знаний по теме и проводится для каждой из двух играющих команд отдельно. Учитель готовит для каждой команды 10–20 теоретических вопросов (определения, формулировки теорем, свойства и т. п.) и задает их последовательно каждому игроку команды. Игрок отвечает на вопрос. Если он не знает ответа, то говорит слово «next» (следующий), и учитель читает следующий вопрос из списка для следующего игрока и т. д., проходя несколько кругов на протяжении 1,5–2 мин. Команде начисляется по 1 баллу за полный и правильный ответ на каждый вопрос.
В проведении этого конкурса третья команда не участвует, а внимательно слушает ответы игроков и помогает ведущему определить, был ответ верным или нет.
Учитель разрабатывает систему штрафных очков: за нерабочий шум — 1 балл; за подсказку — 2 балла; за нарушение других правил — 3 балла и т. д.
В конце каждого конкурса подводятся итоги, и заполняется таблица результатов.
Общее количество баллов за I тур равно разности между суммой набранных командой баллов во всех конкурсах и суммой штрафных баллов.
Очки, набранные в I туре, дают допуск играющим командам во II тур, т. е. они нужны в первую очередь для выявления команды-победительницы I тура.
Предлагаем примерные задания для каждого этапа игры. Игра предназначена учащимся VII класса, проводится по итогам первой четверти и посвящена темам: «Признаки равенства треугольников», «Окружность. Окружность и треугольник», «Функции», «Степень с натуральным показателем».
«Конкурс решения задач»
1. Найти значение выражения
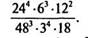
2. Доказать, что на рис. 1
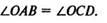
3. Прямая, являющаяся графиком функции, заданной формулой у = кх + А, пересекает оси координат в точках А(0; 6) и B(—4; 0). Найти k и b.
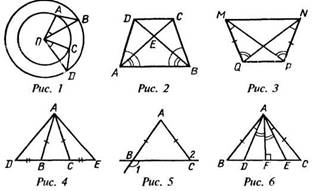
4. Доказать, что на рис. 2 АС = DB.
5. Упростить выражение -(-(-2a3b5)2)3.
6. Доказать по рис. 3, что МР = QN.
7. Записать 260 в виде отношения степеней с основаниями 4 и 8.
8. Доказать, что треугольник DAE на рис. 4 равнобедренный.
9. Решить уравнение 12х — 31 -—+1 = 0.
10. Сравнить углы 1 и 2 на рис. 5.
11. Упростить выражение
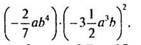
12. Доказать по данным рис. 6, что BE = CD.
13. Расположить в порядке возрастания числа я, а2 и а3, если о < –1.
14. Решить уравнение ׀6х — 12׀ = 8.
«Поименный конкурс»
(Задания сформулированы учениками)
1. Какие из линий треугольника (высоты, медианы, биссектрисы) всегда лежат внутри треугольника? Какие из них могут совпасть с его сторонами?
2. Если в треугольнике провести все медианы, сколько всего треугольников получим?
3. Могут ли высоты треугольника пересекаться в одной из его вершин?
Конкурс «Таинственный конверт»
1. Софизм «2 • 2 = 5».
Рассмотрим уравнение: 5х — 25 + 20 = 4х. Имеем 5х — 25 = 4х — 20. Отсюда 5(х — 5) = 4(х — 5). Разделив обе части на x — 5, получим 5 = 4, т. е. 2–2 = 5. Где мы ошиблись? (О т в е т: разделили на нуль.)
2. Вставить на рис. 7, в подходящее алгебраическое выражение вместо знака вопроса, чтобы выполнялась закономерность, существующая на рис. 7, а и 7, б.
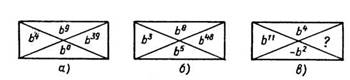
Рис. 7
(Ответ: -А51;
закономерность:
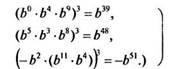
3. Изменив на рис. 8 положение одной спички, получить верное равенство:
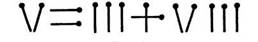
Рис. 8
Ответ: -5 = 3–8.
4. Вставить пропущенное выражение:


5. Какие из точек А(х; 0), В(2х; 0) находятся правее на оси?
Указание. Рассмотреть разные варианты значений для переменной х. (Например: 0<х<1 и др.)
6. Вставить выражение, пропущенное на рис. 9.
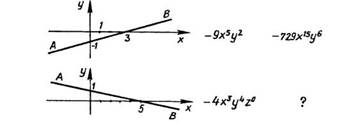
Рис. 9
Ответ: 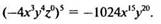
Указание. Первое выражение возводим в степень п, где п определяется как абсцисса точки пересечения прямой АВ с осью Ох.
Конкурс «Next». Задаются подготовленные вопросы каждой команде по очереди.
Литература:
1. Акири И. К. Дидактические игры по математике (на молд. языке). Кишинев: Лумина, 1990.
2. Гайштут А. Г. Математика в логических упражнениях. Киев: Рад. шк., 1985.
3. Саврасова СМ., Ястребинецкий Г. А. Упражнения по геометрии на готовых чертежах. М.: Просвещение, 1987.







