В настоящее время в связи с реформой в Вооруженных Силах России изменились требования к выпускникам военных вузов. Они должны обладать знаниями, умениями и навыками, необходимыми в профессиональной деятельности, уметь самостоятельно принимать решения, быть готовыми к командованию подчиненными. Успешно справиться со всеми задачами и обязанностями будущий офицер сможет, если в процессе обучения у него будут сформированы прочные профессиональные знания и умения.
Повышению качества профессионально-ориентированной подготовки курсантов военных вузов способствует прикладная и практическая направленность обучения математике. Математика как учебный предмет обладает огромным воспитательным и мировоззренческим потенциалом, заключающимся в связях с другими дисциплинами, которые выявляются в учебном процессе при решении прикладных задач (задач с практическим содержанием). Математике в системе подготовки военных инженеров отводится особое место, поскольку без математических знаний невозможно изучение других дисциплин и дальнейшая служба в вооруженных силах. На вооружении современной армии появляется новая боевая техника, основанная на применении электронно-вычислительной техники, высококачественных систем поиска и поражения противника при нанесении точечных ударов, автоматизации развертывания и применения боевой техники. Отсюда следует необходимость формирования у курсантов профессионально-ориентированных математических знаний, т. е. знаний, имеющих направленность на получаемую специализацию по профилю выбранной курсантом специальности. Важную роль в приобретении таких знаний играет мотивация изучения математики, которая формируется посредством решения системы прикладных задач.
Рассмотрим примеры задач ориентированных на реализацию прикладной и практической направленности обучения математике при изучении темы «Обыкновенные дифференциальные уравнения».
Пример 1. Пройденный снарядом путь S в канале ствола орудия и скорость V при ряде допущений связаны между собой выражением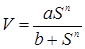 
, где 
, 
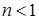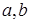— эмпирические коэффициенты. Найти зависимость между временем t движением снаряда и пройденным расстоянием S по каналу ствола.
Решение. Известно, что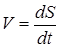 
, тогда 
.
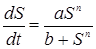Разделим переменные: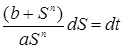 
.
Проинтегрируем
.
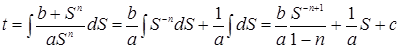Получим общее решение
.
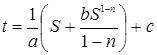При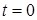 
, 
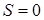получаем 
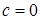. Тогда частное решение имеет вид
.
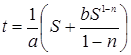Пример 2. Противотанковая граната с массой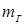 
движется по каналу ствола гранатомета. Скорость ее на срезе ствола 
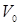(начальная скорость) известна. Эффективная скорость пороховых газов из сопла гранатомета 
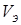— const. Определить массу пороха 
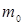, необходимую для придания гранате скорости 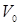на срезе ствола.
Замечание. Уравнение, описывающее движение гранаты в канале ствола гранатомета, имеет вид 
, (1)
где 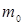— масса пороха; 
, 
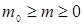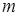меняется от 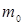до 0 (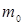–масса порохового стартового заряда); 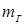— масса гранаты, 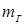— const.
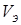— эффективная скорость истечения пороховых газов, 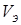— const.
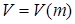— скорость движения гранаты в канале ствола гранатомета.
Начальные условия: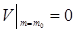 
. (2)
Решая уравнение (1) при начальных условиях (2), получим:
; 
;
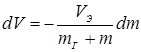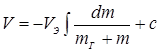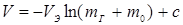, где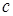 
— const;
; 
; 
.
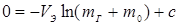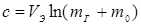Используя условие задач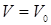и (
при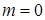 
), получим:
.
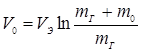Преобразуем правую часть, применяя приближенное равенство:
, 
,
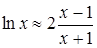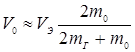откуда найдем :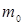 
.
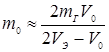Пример 3. (задача о потери тепла в окружающую среду). Цилиндрический бак, покрытый асбестовой изоляцией, расположен горизонтально на эстакаде и применяется как приемник для выдержки продуктов химической реакции. Температура T массы жидкости, помещенной в этот бак, в любой момент времени t можно найти их дифференциального уравнения:
,
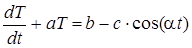где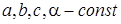 
, зависящие от габаритов бака, качества асбеста и жидкости.
Решение. Данное дифференциальное уравнение линейное первого порядка. Решим его методом Бернулли:
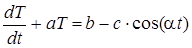
Замена: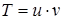 
, 
.
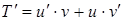Получаем: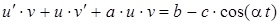 
, или
;
; 
; 
; 
.
; 
;
.
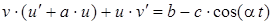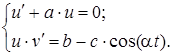
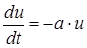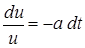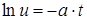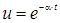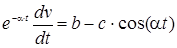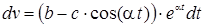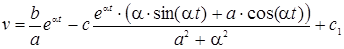При нахождении функции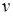 
пользовались табличным интегралом:
.
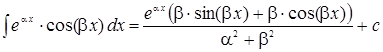Подставляя найденные значения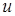 
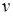и в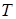 
, получим:
.
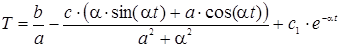Конечно, решение одной или двух задач прикладного или практического содержания по теме не способствует формированию мотивации изучения математики и тем более формированию профессиональных умений. Только систематическое и целенаправленное решение задач прикладного содержания является средством формирования профессионально значимых качеств личности.
Безусловно, направленность курса математики на профессиональную деятельность служит важным фактором ориентации на будущую специальность. Демонстрация возможности применения дифференциальных уравнений при решении прикладных и практических задач усиливает мотивационную составляющую учебного процесса, способствует формированию знаний и умений, необходимых для решения задач возникающих в профессиональной деятельности. Кроме того, прикладная и практическая направленность преподавания математики в военном вузе способствует системности знаний курсантов, вносит вклад в развитие их мировоззрения, повышая качество профессиональной подготовки.
Литература:
1. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Построение математических моделей в прикладных задачах // Молодой ученый. — 2013. — № 12(59) — с. 3–6.
2. Куимова Е. И., Куимова К. А., Ячинова С. Н. Формирование мотивационной составляющей обучения на примере изучения дифференциальных уравнений // Молодой ученый. — 2014. — № 2(61) — с.775–777.
3. Ячинова С. Н., Гудкова В. С. Мотивация обучения студентов посредством моделирования // Молодой ученый. — 2014. — № 4 — с.1141–1144.
