Задачи дисциплины «Математические методы и модели в расчетах на ЭВМ» состоят в ориентировании студентов на использование математических понятий, методов моделирования и оптимизации процессов в профессиональной деятельности.
Процесс изучения дисциплины направлен на формирование следующих компетенций:
- использование основных законов естественнонаучных дисциплин в профессиональной деятельности, применение методов математического анализа и моделирования, теоретического и экспериментального исследования (ОК-10);
- готовность эксплуатировать технологическое оборудование (ПК-2);
- готовность идти на умеренный риск (ПК-12);
В результате изучения дисциплины студент должен:
- знать: основные логические исчисления; методы и процессы сбора и переработки информации;
- уметь: использовать математические методы и модели в технических приложениях, самостоятельно формулировать задачу научного исследования, наметить пути ее решения, расширять свои математические познания;
- владеть: методами организации вычислительных экспериментов в области профессиональной деятельности.
Формирование компетенций в учебном процессе возможно осуществить посредством профессионально-ориентированных задач [1,2]. В качестве примера рассмотрим задачу об использовании ресурсов.
Пример. Предприятие выпускает два вида продукции, используя при этом три вида сырьевых ресурсов. Нормы затрат сырья, его запасы, а также доход получаемый от выпуска единицы продукции приведены в таблице 1.
Таблица 1
|
Виды сырья |
Нормы затрат на единицу продукции, кг |
Запасы сырья, кг |
|
|
продукция 1 вида |
продукция 2 вида |
||
|
Р1 |
10 |
14 |
182 |
|
Р2 |
20 |
20 |
360 |
|
Р3 |
58 |
29 |
696 |
|
Доход от единицы продукции |
4 |
3 |
|
Требуется определить такой план выпуска продукции вида 1 и 2, при котором будет получен максимальный доход предприятия.
Составим математическую модель задачи. Количество изделий продукции 1-го вида обозначим за x1, количество изделий продукции 2-го вида обозначим за x2.
Найдем максимальное значение целевой функции
Z = 4x1+3x2 → max,
при системе ограничений:
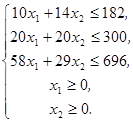(1)
Решим задачу с помощью программы Microsoft Excel. Ввод исходных данных показан на рис.1.
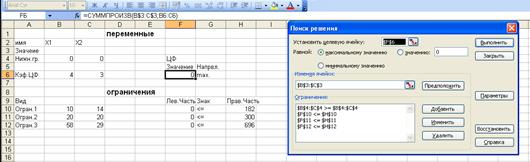
Рис. 1. Ввод исходных данных.
Результаты расчета представлены на рис.2.
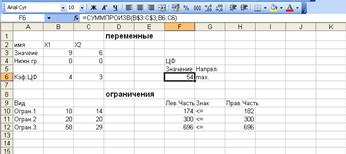
Рис. 2. Результаты расчета
Считаем целесообразным при организации учебного процесса при изучении дисциплины «Математические методы и модели в расчетах на ЭВМ» решение оптимизационных задач произвести сначала «вручную». Такой прием позволяет наглядно рассмотреть поиск оптимального решения.
Приведем решение исходной задачи графическим методом. Для этого построим многоугольник решений (построим каждую прямую и определим полуплоскости, заданные неравенствами):
L1:10x1+14x2=182,
L2:20x1+20x2=300,
L3:58x1+29x2=696,
L4:x1=0,
L5:x2=0.
В пересечении полуплоскостей получим многоугольник решений ABCDE (рис.3).
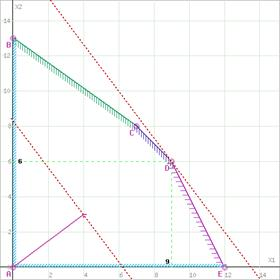
Рис. 3. Многоугольник решений.
Построим линию уровня, отвечающую значению функции Z = 0 (4x1+3x2 = 0). Вектор-градиент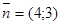 
, составленный из коэффициентов целевой функции, указывает направление максимизации Z(X). Передвинем линию уровня в направлении вектора 
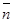параллельно самой себе до последнего касания обозначенной области в точке D, т. к. нас интересует максимальное решение (на графике эта прямая обозначена пунктирной линией). Точка D лежит на пересечении прямых L2, L3 и имеет следующие координаты:
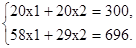
Решив систему уравнений, получим: x1 = 9, x2 = 6. Найдем максимальное значение целевой функции Z в точке D (Z = 4x1+3x2):
Z(D) = 4*9 + 3*6 = 54=Zmax.
Следует отметить, что графический метод наглядно демонстрирует возможные варианты решений, но имеет строгое ограничение по количеству переменных. Поэтому рекомендуется решить исходную задачу симплексным методом. Приведем систему ограничений (1) к каноническому виду путем добавления неотрицательных переменных x3, x4, x5:
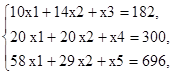
при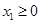 
, 
.
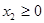На начальном этапе решения основные переменные: x3, x4, x5, неосновные переменные: x1, x2. Полагая неосновные переменные x1=0, x2=0 получим первое базисное решение x3=182, x4=300, x5=696, которое соответствует начальной точке А многоугольника решений ABCDE (рис.3):
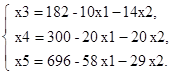
Увеличим значение целевой функции Z переводом из неосновных в основные переменной x1 (в качестве разрешающего примем третье уравнение):
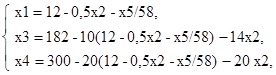
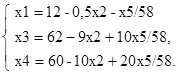
Произведен переход в точку E (рис.3). Основные переменные: x1,x3, x4, неосновные переменные: x5, x2. Полагая неосновные переменные x5=0, x2=0 получим второе базисное решение x1=12, x3=62, x4=60 (Z(Е) = 4x1+3x2=4∙12+3∙0=48).
Увеличим значение целевой функции Z переводом из неосновных в основные переменной x2 (в качестве разрешающего примем третье уравнение):
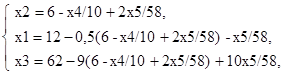
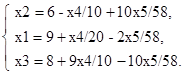
Произведен переход в точку D (рис.3). Основные переменные: x1, x2, x3, неосновные переменные: x4, x5. Полагая неосновные переменные x4=0, x5=0 получим решение x1=9, x2=6, x3=8 при котором Z(D) = 4x1+3x2=4∙9+3∙6=54=Zmax.
Данный метод позволяет проследить и оценить возможные значения целевой функции при прохождении по точкам многоугольника решений ABCDE (рис.3). Заметим, что симплексный метод является универсальным методом, которым можно решать любую задачу линейного программирования.
Предложенный метод организации учебного процесса позволяет студентам оценить, выделить преимущества каждого метода решения предлагаемой задачи и выбрать наиболее оптимальный [3,4,5].
Выстроенный таким образом учебный процесс, на наш взгляд, в полной мере соответствует новым образовательным стандартам и способствует формированию профессиональных компетенций.
Литература:
1. Бочкарева, О. В. Математические задачи как средство формирования профессиональных качеств личности / О. В. Бочкарева, Т. Ю. Новичкова, О. В. Снежкина, Р. А. Ладин // Современные проблемы науки и образования.–2014.–№ 2; URL: www.science-education.ru/116–12584
2. Ладин, Р. А. Математика и междисциплинарные связи/Р. А. Ладин, О. В. Снежкина, О. В. Бочкарева, Н. В. Титова//Молодой ученый.- 2014.- № 1.- С. 550–552.
3. Бочкарева, О. В. Формирование профессиональных умений на занятиях по математике/ О. В. Бочкарева, О. В. Снежкина, М. А. Сироткина // Молодой ученый.- 2014.- № 2 (61).- С. 735–738.
4. 4 Ладин, Р. А. Математика в учебном процессе строительного вуза/ Р. А. Ладин, О. В. Снежкина, Г. А. Левова //Вестник магистратуры.- 2013.- № 12–4 (27).- С. 56–59.
5. Сироткина, М. А. К вопросу о профессиональной направленности обучения математике / М. А. Сироткина, О. В. Бочкарева, О. В. Снежкина // Вестник магистратуры.- 2014.- № 2 (29).-С. 59–61.
