Для снижения поврежденности хлопковых волокон и семян хлопка-сырца целесообразном является снижение кратности взаимодействия рабочих органов с хлопком в процессе первичной обработки хлопка. При этом важным является повышение эффективности взаимодействия хлопка с рабочими органами за счет совершенствования их конструкции. Нами рекомендуется новая конструкция колосниковой решетки очистителя хлопка от крупного сора [1].
При этом в рекомендуемой конструкции колосника значительно уменьшается сопротивление от трения о боковые поверхности с хлопком — сырцом. Кроме того, упругие втулки 4 установлены эксцентрично в боковинах 3 колосниковой решетки. При этом фактически упругость опор будет иметь нелинейный характер. Согласно известной методики в работе [3] упругий элемент можно представить как коническую пружину с нелинейной жесткостью (см. рис.1). На рис. 1. а представлены установки конических колосников 1 на упругих опорах 2 в боковинах 3. При этом упругие втулки 2 выполнены также эксцентричными, имеют переменную толщину. Следует отметить, что в процессе работы положение эксцентриситета может меняется (имеются некоторые круговые движения). Поэтому величина эксцентриситета 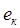 и разница диаметров конических колосников 1 не превышают (2,0¸3,0)10–3м. При среднем значении диаметра колосника
и разница диаметров конических колосников 1 не превышают (2,0¸3,0)10–3м. При среднем значении диаметра колосника 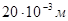 . Согласно расчетной схемы (см.рис.1.) составим уравнение описиваюшее колебание колосника. Известно, что на колосник действует случайная возмущающая сила со стороны протискиваемого хлопка — сырца
. Согласно расчетной схемы (см.рис.1.) составим уравнение описиваюшее колебание колосника. Известно, что на колосник действует случайная возмущающая сила со стороны протискиваемого хлопка — сырца
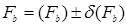 (1)
(1)
где, 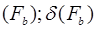 - математическое ожидание сопротивления от хлопка-сырца и его случайное составляющее.
- математическое ожидание сопротивления от хлопка-сырца и его случайное составляющее.
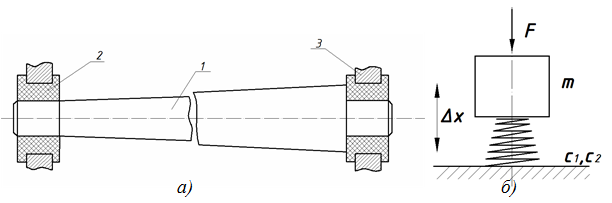
Рис.1. Схема конических колосников на упругих опорах и расчетная схема: а) цельная коническая колосниковая решетка на упругих опорах с нелинейной жесткостью; б) расчетная схема колебаний конического колосника; 1- конические колосники, 2- резиновая втулка с переменной толщиной, 3-корпус (боковина, сегмент) колосниковой решетки
Следует отметить, что жесткость упругой опоры имеет нелинейный характер и восстанавливающая сила определяется из выражения
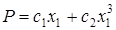 (2)
(2)
где, с2, с1 — значения коэффициентов жесткости упругой опоры;
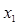 — перемещения колосника в вертикальном направлении.
— перемещения колосника в вертикальном направлении.
Колебания колосника описывается следующим дифференциальным уравнением
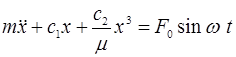 (3)
(3)
где, 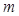 — приведенная масса колосника;
— приведенная масса колосника; 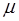 -постоянный коэффициент нелинейности;
-постоянный коэффициент нелинейности;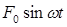 - возмущающая сила от протаскиваемого хлопка-сырца.
- возмущающая сила от протаскиваемого хлопка-сырца.
Решение уравнения (3) ищем по методу Галеркина [4] в виде
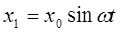 (4)
(4)
Подставив выражение (4) в дифференциальное уравнение (3) и учитывая интеграл равном нулю имеем
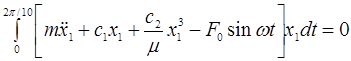
где, 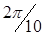 — период колебаний.
— период колебаний.
После интегрирования получим
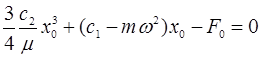 (5)
(5)
Корни уравнения (5) удобно определить графически, построив графики функций [4]:
Графическое решение задачи (5)

Рис. 2.
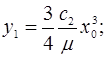
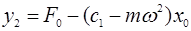 (6)
(6)
Решение задачи (5) представлена на рис.2.
Аналитическим условием совпадения двух действительных корней кубического уравнения является условие
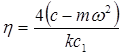 где,
где, 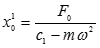
А = 0 при 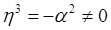
где, 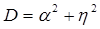 ;
; 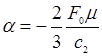 ;
;
Откуда можно определить значения 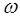 [4]:
[4]:
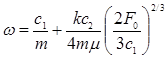
При этом корни уравнения (5) будут
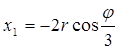 ;
; 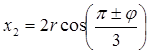
где, 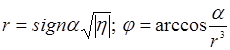
Для конкретных значений параметров можно выбирать по рекомендуемой методике необходимые значения амплитуды и частоты нелинейных колебаний колосника. Рассмотрим известный метод решения задачи [4].
Уравнение (3) перепишем в виде
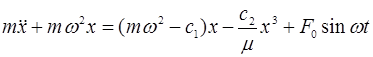 (7)
(7)
Используя метод Дуффинга [5], получим решение в качестве первого приближения величину
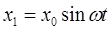 (8)
(8)
Окончательно приближенное решение имеет вид
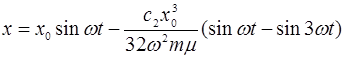 (9)
(9)
При этом значение х0 определяется из уравнения. С учетом исходных значений параметров системы были получены закономерности колебательного движения колосников на упругих опорах с нелинейной жесткостью. На основе обработки полученных результатов построены графические зависимости размаха колебаний колосника при вариации среднего значения коэффициента жесткости упругой опоры, массы колосника при 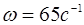 и
и 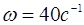
Анализ графиков показывает, что с увеличением жесткости упругой опоры Dх уменьшается по нелинейному закону, причем с уменьшением 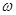 снижение Dх становится интенсивнее. При увеличении массы колосника влияние
снижение Dх становится интенсивнее. При увеличении массы колосника влияние 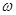 на уменьшение Dх становится незначительным. Это объясняется тем, что при большой массы колосника повышается его инерционность и значение Dх стремится к постоянной величине (2,0–2,4 мм). Именно при этих значениях Dх очистительный эффект становится ощутимым, что подтверждено результатами экспериментов [2].
на уменьшение Dх становится незначительным. Это объясняется тем, что при большой массы колосника повышается его инерционность и значение Dх стремится к постоянной величине (2,0–2,4 мм). Именно при этих значениях Dх очистительный эффект становится ощутимым, что подтверждено результатами экспериментов [2].
Таким образом, используя предложенный метод можно обосновать необходимые параметры системы, обеспечивающие повышение эффекта очистки очистителей хлопка-сырца, от крупного сора.
Литература:
1. Мирахмедов Д. Ю., Холтураев Х. П., А.Дж.Джураев. Колосниковая решётка очистителя волокнистого материала. Патент Рес. Узб. FAP 00428, Бюлл. № 12 2008.
2. А.Джураев А. В. Абдуллаев. Дж.Мирахмедов. Экспериментальное определение нагружённости конических колосников на упругих опорах очистителя хлопка. Ж. Проблемы текстиля № 3, 2010 г. Ташкент, С.7–10
3. Джураев А. Д. и др. Динамика вибрирующих рабочих органов очистителей хлопка — сырца, «ФАН», Ташкент, 2003, 192с.
4. Светлицкий В. А., Стасенко И. В., Сборник задач по теории колебаний. Высшая школа, М., 1973, 456с.
5. Расулов Р. Х. Обоснование параметров пильчато — колосниковой системы очистителя хлопка — сырце от крупного сора. Канд. дисс., Ташкент, 2008г, 130с.







