Разгрузка кинематических пар кривошипно-ползунного механизма иглы

Для определенности изложения все выкладки сделаны для плоского центрального кривошипно-ползунного механизма.

Движение точки В ползуна будем рассматривать в неподвижной системе отсчета XB₂Y. Определим ускорение точки В ползуна в крайних ее положениях B₁ и В₂, полагая, что кривошип вращается равномерно со скоростью .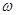

Из рис. 1 можно получить зависимость между скоростями точек B и A:

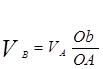
где: Ob — отрезок, отсекаемый на прямой OY₁ являющится продолжением оси симметрии шатуна.

Ускорение точки B можно определить выражением:

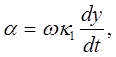
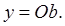
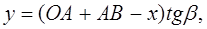
то

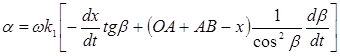                                                  (1)

где: k₁ — масштабный коэффициент для y=Ob

Из формулы (1) видно, что

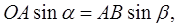
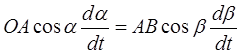
поэтому:

для правого крайнего положения точки В имеем:

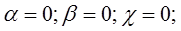
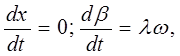
где: 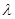= r / l — геометрический параметр механизма.

Аналогично:

для левого крайнего положения точки В имеем:

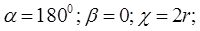
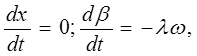
В соответствии с этим по формуле (1) найдем ускорения точки В ползуна в правом и левом крайних положениях:

 

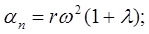
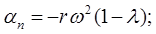
Как известно, график функции имеет вид:

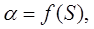
где: S = k₁x, — можно с достаточной точностью принять за параболу, которая проходит через точк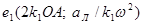и  и 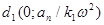, а касательные к параболе в этих точках пересекаются в точке 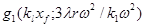, где:  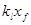представляет абсциссу точки пересечения прямой d₁e₁ с осью направляющей (рис. 2).

Уравновешивание вращающихся масс.

Центр масс подвижных звеньев механизма определим вектором

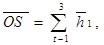
где: 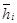 — вектор главной точки i-го звена.

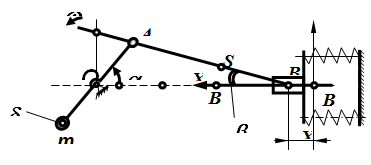
Рис. 1. Схема  механизма иглы с упругой связью

 

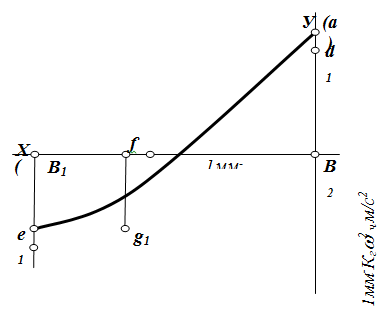
Рис. 2. График измения зависимости перемещения иглы от ускорения

 

Если векторы 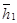 и 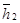 главных точек кривошипа и шатуна удовлетворяют пропорции

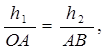                                                                                                            (2)

то справедливо равенство

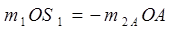
представляющее условие уравновешенности вращающихся масс, к которым относятся масса т₁ кривошипа (рис. 2) и часть массы т₂ шатуна, приведенная статически к точке А кривошипа и равная

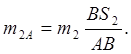
Таким образом, для реализации условия (2), кривошипу необходимо придать такую форму, чтобы его дисбаланс относительно оси вращения был:

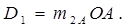
Если последнее условие выполняется, то центр масс подвижных звеньев механизма будет двигаться вдоль оси направляющей с ускорением 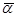. Поэтому по оси направляющей будет действовать неуравновешенная сила

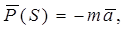                                                                                                        (3)

где:

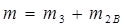
представляет поступательно движущуюся массу, состоящую из массы т₃ ползуна и шатунной массы

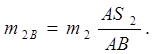
Разгрузка кинематических пар от действия силы 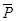(S). Сила 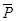(S)будет вызывать динамические давления в кинематических парах механизма, которые могут создавать не только отмеченные выше отрицательные явления, но в некоторых случаях служить основным препятствием для повышения производительности машины.

Чтобы полностью разгрузить вращательные пары от действия силы 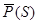, необходимо установить между ползуном и стойкой упругую связь с такой характеристикой Q(S), чтобы удовлетворялось условие:

Q(S) = -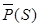                                                                                                                (4)

при любой частоте вращения кривошипа.

Однако сила 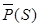 (2.3) является существенно нелинейной и зависит не только от абсциссы точки В ползуна, но и от частоты вращения кривошипа. По этой причине, реализация равенства (2.4) встречает в общем случае значительные конструктивные трудности. Решим локальную задачу о частичной разгрузке кинематических пар механизма упругой связью с линейной характеристикой при некоторой номинальной частоте вращения кривошипа.

 

Литература:

 

1.         Лебедев В. С. Технологические процессы машин и аппаратов в производствах бытового обслуживания. -М.: Легпромбытиздат, 1991. -331 с.

2.         Макаров А. И., Крылов В. В. и др. Расчет и конструирование машин прядильного производства. -М.: Машиностроение, 1981. — 464 с.

3.         Маракушев Е. А. и др., Машины швейного производства. Конструкция, расчет и основы проектирования. –Киев, Техника, 1967. — 324 с.