В статье рассматривается способ применения интеллектуальных нейросетевых технологий для анализа многомерных данных в пакете Matlab. Построена нейросетевая модель, адекватно воспроизводящая статистические данные.
Ключевые слова: нейронная сеть, интеллектуальные технологии, анализ многомерных данных.
Одной из важнейших задач математического моделирования деятельности любого предприятия является оценка его финансового состояния на основе статистических данных за отчетный период. Для составления описания деятельности предприятия применяют экономико-математические и статистические методы анализа, позволяющие получать математические модели, наиболее приближенные к эмпирическим данным.
В настоящее время одним из перспективных направлений моделирования экономических процессов является использование искусственных нейронных сетей, которые позволяют найти решение быстрее и эффективнее по сравнению с известными алгоритмами моделирования. Одним из преимуществ применения нейросетей является их способность работать с неполной информацией [1, с. 170].
Нейронная сеть — это система, состоящая из многих простых вычислительных элементов, или нейронов, определенным образом связанных между собой. Наиболее распространенными являются многослойные сети, в которых нейроны объединены в слои. Слой, в свою очередь, представляет собой совокупность нейронов, на которые в каждый момент времени параллельно поступает информация от других нейронов сети, т. е. выходы нейронов соединяются с входами других нейронов. После того как определено количество слоев и число элементов в каждом из них, нужно обучить сеть, т. е. найти значения для весов и порогов сети, которые минимизировали бы ошибку прогноза, выдаваемого сетью. Для этого существуют так называемые алгоритмы обучения. Ошибка для конкретной конфигурации сети определяется путем прогона через сеть всех имеющихся наблюдений и сравнения реально выдаваемых выходных значений с желаемыми (целевыми) значениями. По сути, процесс обучения представляет собой подгонку модели, которая реализуется сетью, к имеющимся обучающим данным [2, с. 34].
Построим нейросетевую модель финансовых показателей для предприятия ОАО «Башинформсвязь», которое является одним из крупнейших операторов связи в уральском регионе и в стране. Статистические данные для построения модели взяты поквартально за период с 2006 года по 2013 год [3].
Значение чистой прибыли, в руб., от влияющих на нее факторов обозначим за 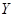 — это зависимая переменная. В качестве объясняющих переменных возьмем следующие факторы, в рублях:
— это зависимая переменная. В качестве объясняющих переменных возьмем следующие факторы, в рублях: 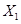 — выручка;
— выручка; 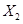 — себестоимость реализованных товаров и услуг;
— себестоимость реализованных товаров и услуг; 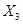 – коммерческие расходы;
– коммерческие расходы; 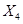 – прочие операционные доходы;
– прочие операционные доходы; 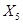 — прочие операционные расходы;
— прочие операционные расходы; 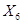 — дебиторская задолженность;
— дебиторская задолженность; 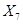 – отложенные налоги;
– отложенные налоги; 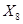 — нераспределенная прибыль.
— нераспределенная прибыль.
Для выявления взаимосвязи между всеми переменными проведен корреляционный анализ. На основе анализа матрицы коэффициентов парной корреляции из модели исключаются такие факторы, как 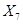 и
и 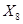 .
.
Для построения нейросетевой модели использовано 6 входных факторов (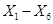 ), 1 выходное значение (
), 1 выходное значение (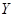 ), 31 наблюдение. Для получения достоверных результатов необходимо использовать нейросеть, аппроксимирующую исходные данные с максимальной степенью точности. Выбор архитектуры сети для решения конкретной задачи основывается на опыте разработчика. Для получения наилучшей сети проведем ряд экспериментов. Построим в Matlab нейросети с обратным распространением ошибки, т. к. они обладают хорошими обобщающими свойствами. Изменяя число скрытых слоев, число нейронов в слоях, функции активации нейронов выберем сеть с наилучшим значением общей среднеквадратической ошибки.
), 31 наблюдение. Для получения достоверных результатов необходимо использовать нейросеть, аппроксимирующую исходные данные с максимальной степенью точности. Выбор архитектуры сети для решения конкретной задачи основывается на опыте разработчика. Для получения наилучшей сети проведем ряд экспериментов. Построим в Matlab нейросети с обратным распространением ошибки, т. к. они обладают хорошими обобщающими свойствами. Изменяя число скрытых слоев, число нейронов в слоях, функции активации нейронов выберем сеть с наилучшим значением общей среднеквадратической ошибки.
Создадим двухслойную однонаправленную сеть, предварительно нормализуя исходные значения финансовых показателей. Первый слой состоит из 20 нейронов с функциями активации 'tansig', второй слой содержит 1 нейрон с функцией активации 'purelin'. Для обучения воспользуемся алгоритмом Левенберга-Маркара ('trainlm'):
net=newff([-2.146 1.526; -1.140 2.498; -1.498 2.264; -2.591 2.130; -2.177 2.698],
[20 1],{'tansig' 'purelin'});
Обучим созданную сеть, используя функцию train:
net=train(net,INP,OUTP),
где INP — сформированный входной вектор из обучающей выборки, а OUTP — сформированный выходной вектор из обучающей выборки.
Для моделирования нейронной сети воспользуемся функцией sim:
Y = sim(net,X),
где net — сеть, X — вектор входных сигналов, Y — вектор выходных значений сети.
Для оценки качества сети рассчитана общая среднеквадратическая ошибка, значение которой менее 0,05 считается удовлетворительным [4, с. 1575].
Построим 9 нейросетей с одним скрытым слоем, изменяя типы функции активации и число нейронов от 7 до 20. Значения среднеквадратической ошибки этих сетей приведены в табл. 1.
Таблица 1
Значение среднеквадратической ошибки для нейросетей с одним скрытым слоем
|
Номер нейросети |
Функция активации нейронов скрытого слоя/ выходного слоя |
Количество нейронов в скрытом слое |
Значение среднеквадратической ошибки |
|
1 |
Tansig/ Purelin |
7 |
0,052 |
|
2 |
17 |
0,013 |
|
|
3 |
20 |
0,009 |
|
|
4 |
Logsig/ Purelin |
7 |
0,083 |
|
5 |
17 |
0,046 |
|
|
6 |
20 |
0,031 |
|
|
7 |
Purelin/ Purelin |
7 |
0,085 |
|
8 |
17 |
0,091 |
|
|
9 |
20 |
0,097 |
На рис. 1 приведен график зависимости среднеквадратической ошибки от количества нейронов в скрытом слое. Отсюда видно, что для нейросетей № 1–6 с увеличением числа нейронов скрытого слоя ошибка уменьшается, а для нейросетей № 7–9, наоборот, увеличивается.
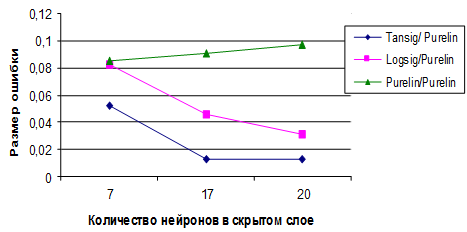
Рис. 1. График зависимости среднеквадратической ошибки от количества нейронов
Построим нейронные сети с двумя скрытыми слоями. В табл. 2 приведены значения среднеквадратических ошибок для нейросетей с двумя скрытыми слоями, количество нейронов на слое изменяется от 2 до 6, используются функции активации Tansig/ Tansig /Purelin и Logsig/ Tansig /Purelin.
Таблица 2
Значение среднеквадратической ошибки для нейросетей с двумя скрытыми слоями
|
Номер нейросети |
Функция активации нейронов 1 скрытого слоя/2 скрытого слоя/ выходного слоя |
Количество нейронов в 1 скрытом слое |
Количество нейронов во 2 скрытом слое |
Значение среднеквадратической ошибки |
|
1 |
Tansig/ Tansig /Purelin |
2 |
2 |
0,085 |
|
2 |
4 |
4 |
0,028 |
|
|
3 |
2 |
6 |
0,043 |
|
|
4 |
Logsig/ Tansig /Purelin |
2 |
2 |
0,084 |
|
5 |
4 |
4 |
0,025 |
|
|
6 |
2 |
6 |
0,039 |
Из рисунка 2 видно, что размер ошибки для сетей с функциями активации Logsig/ Tansig /Purelin ниже, чем для аналогичных сетей с функциями Tansig/ Tansig /Purelin.
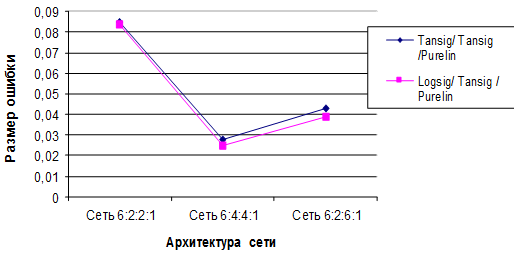
Рис. 2. График зависимости размера среднеквадратической ошибки от количества нейронов в скрытых слоях
Анализ полученных данных показал, что наилучшей сетью является сеть с архитектурой 6:20:1 (6 входных нейронов, 20 нейронов на 1 скрытом слое и 1 выходное значение), функциями активации Tansig/Purelin (среднеквадратическая ошибка равна 0,009). На рис. 3 представлены фактические значения финансовых показателей и значения, предоставляемые нейросетевой моделью.
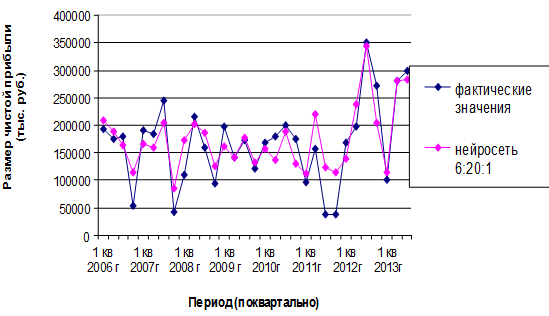
Рис. 3. Динамика чистой прибыли ОАО «Башинформсвязь»
Коэффициент детерминации R2, рассчитанный для нейросетевой модели 6:20:1, равен 0,971, что свидетельствует о том, что нейронная сеть достаточно хорошо описывает связь между входными и выходными значениями модели.
Таким образом, построенную нейросетевую модель финансовых показателей можно использовать для решения задач прогнозирования величины чистой прибыли и оптимизации финансовых показателей предприятия.
Литература:
1. Кравченко М. Л., Грекова Т. И. Моделирование экономических систем с применением нейронных сетей // Вестник Томского государственного университета, 2006. — № 290. — С. 169–172.
2. Степашина Е. В. Оптимизация финансовых показателей предприятия на основе нейросетевой модели // Информационные системы и технологии, 2014. — № 5. — С. 34–42.
3. Бухгалтерский баланс и приложения к нему ОАО «Башинформсвязь» [Электронный ресурс]. — URL: http://www.bashtel.ru/buh_ballance.php.
4. Antipin A. F. A Computer-aided System for Designing Multidimensional Logic Controllers with Variables Representing a Set of Binary Logic Arguments // Automation and Remote Control, 2013. — No 9. — Vol. 74. — P. 1573–1581.







