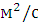Руководствуясь исследованиями (1, 2, 3, 4, 5), проделанными в этой области, нами сделана попытка определения расчетным путем силы удара волокнистой частицы различной массы /от 0,00075 кг до 0,000125 кг/ о направители колосников новой конструкции с учетом динамической жесткости прядки, от которой зависит время и максимальная величина силы удара.
Составляем уравнения для упругой модели с одной степенью свободы с учетом жесткостных характеристик без диссипации энергии
Рmax = K X (1)
где К — коэффициент жесткости прядки, кгс-2;
X — деформация.
Из формулы (1) и учитывая, что х =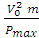
имеем
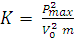(2)
Для одномассовой системы с одним упругим элементом /с одной степенью свободы/ без учета диссипации энергии известно
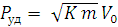(3)
Данные таблицы 1 полностью согласуются с этой формулой с незначительной разницей между экспериментальными и теоретическими результатами из — за наличия, вообще говоря, слабой нелинейности.
Результаты экспериментов по определению параметров удара и расчетные характеристики линейной модели
Таблица 1
|
Скорость летучки /барабана/ |
Вес клочка, кг |
Сила удара, Н |
Время нарастания нагрузки, С |
Общее время удара, с |
Коэффициент жесткости, кгс-2 |
Расчетная сила удара, Н |
|
7,7
10,8
11,5
13,8
15,4 |
0,000125
0,000125
0,000125
0,000125
0,000125 |
0,0669
0,0743
0,0915
0,1194
0,134 |
0,0157
0,0143
0,0122
0,0105
0,0101 |
0,0423
0,0572
0,0491
0,0422
0,0414 |
0,695
0,376
0,51
0,693
0,625 |
0,0717
0,074
0,092
0,129
0,136 |
Кроме того, можно найти динамическую жесткость прядки, используя формулу
К =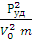 
(4)
С использованием ЭВМ получены значения К для различных скоростей и силы удара.
Из табл. 1 очевидно, что
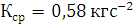
Для линейной модели известно
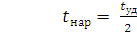(5)
откуда
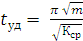(6)
Однако, судя по формуле, общее время удара может быть равно сумме времени нарастания нагрузки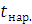 
и времени спадания нагрузки 
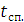, но больше, чем значения 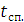больше, чем значения 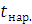, что показывает послеударное затухание средств измерения, зависящее от свойств металла и размеров клочка /прядки/ (рис. 1)
Реальный клочок — система нелинейная и t убывает с ростом скорости, что говорит о том, что между силой и диссипацией клочка имеется нелинейная зависимость в виде
Р = схn (7)
где n > 1
По данным Бурнашева Р. З.
n = 1,1 + 1,4
для хлопка-сырца и нет никаких оснований считать, что здесь n иное — то же волокно и та же тенденции к уменьшению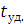 
с ростом 
.
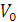Модель по формуле (7) решается, но удобнее с погрешностью до 20 % в инженерной сценке считать клочок линейной системой.
Об этом свидетельствуют и данные таблицы 1, где приведены расчетные значения силы удара.
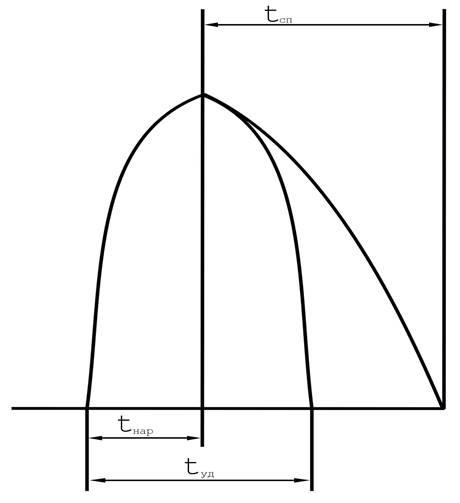
Рис. 1. Характеристика осциллограммы ударного взаимодействия клочка волокна с направителем
Литература:
1. Сафаев А. А. «Повышение эффективности хлопка-сырца тонковолокнистых сортов совершенствованием ударно рыхлительних устройств очистителей мелкого сора».
2. Исмаилов А. А. «Повышение эффективности очистки хлопкового волокна».
3. Лугачев А. Е. «Исследование основных элементов очистителей хлопка-сырца с целю повышения качественных показателей хлопка-сырца».
