Метод бисекции или метод деления отрезка пополам — простейший численный метод для вычисления корней уравнения вида f(x)=0 на интервале [a;b], учитывая то, что функция на данном отрезке непрерывна и меняет знак. Графически это показано на рисунке 1.
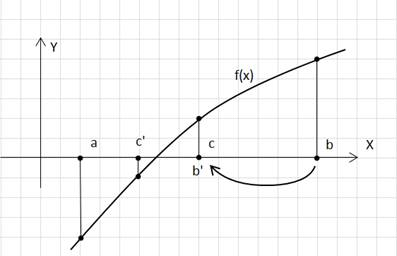
Рис. 1. Графическое изображение метода бисекции
Общая схема работы алгоритма следующая:
1. Выбираем такие a и b, что f(a) и f(b) имеют разные знаки.
2. Вычисляем c=(a+b)/2.
3. Сравниваем знаки функций f(a), f(b), f(с).
4. Производим перенос одной из точек a или b в точку с, в которой знак функции f(c) совпадает со знаком f(a) или f(b).
5. Проверяем условие модуль(f(c))<e, где e — требуемая точность.
6. Если требуемая точность не достигнута, то возвращаемся к пункту 2.
Данный метод дает следующее приближение к корню: 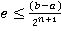 , где n — количество итераций. Метод имеет сходимость по закону геометрической прогрессии с коэффициентом 1/2. Данный алгоритм можно реализовать на языке программирования или создать модель в математическом пакете, табличном процессоре.
, где n — количество итераций. Метод имеет сходимость по закону геометрической прогрессии с коэффициентом 1/2. Данный алгоритм можно реализовать на языке программирования или создать модель в математическом пакете, табличном процессоре.
Интересно выглядит работа алгоритма в двоичной системе счисления. Чтобы приблизиться к теме вычисления значения квадратного корня в двоичной системе счисления, проанализируем работу алгоритма в десятичной системе.
Для вычисления квадратного корня 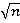 требуется решить уравнение вида
требуется решить уравнение вида 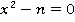 . Для поиска корня воспользуемся исследуемым методом. Корень лежит в интервале
. Для поиска корня воспользуемся исследуемым методом. Корень лежит в интервале 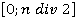 . В таблице 1 представлены результаты расчета. В таблице показаны первые 40 шагов итерации для исследования точности вычислений. К 40-му шагу итерации достигается точность 10 десятичный знаков.
. В таблице 1 представлены результаты расчета. В таблице показаны первые 40 шагов итерации для исследования точности вычислений. К 40-му шагу итерации достигается точность 10 десятичный знаков.
Таблица 1
Результаты вычисления 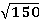
|
№ итерации |
a |
b |
c=(a+b)/2 |
c2 |
Абсолютная погрешность |
|
1 |
0,0000000000 |
75,0000000000 |
37,5000000000 |
1406,2500000000 |
25,2525512861 |
|
2 |
0,0000000000 |
37,5000000000 |
18,7500000000 |
351,5625000000 |
6,5025512861 |
|
3 |
0,0000000000 |
18,7500000000 |
9,3750000000 |
87,8906250000 |
2,8724487139 |
|
4 |
9,3750000000 |
18,7500000000 |
14,0625000000 |
197,7539062500 |
1,8150512861 |
|
5 |
9,3750000000 |
14,0625000000 |
11,7187500000 |
137,3291015625 |
0,5286987139 |
|
… |
… |
… |
… |
… |
… |
|
11 |
12,2314453125 |
12,3046875000 |
12,2680664063 |
150,5054533482 |
0,0206176923 |
|
… |
… |
… |
… |
… |
… |
|
16 |
12,2451782227 |
12,2474670410 |
12,2463226318 |
149,9724180030 |
0,0011260821 |
|
17 |
12,2463226318 |
12,2474670410 |
12,2468948364 |
149,9864331345 |
0,0005538775 |
|
18 |
12,2468948364 |
12,2474670410 |
12,2471809387 |
149,9934409458 |
0,0002677752 |
|
… |
… |
… |
… |
… |
… |
|
29 |
12,2474486008 |
12,2474488802 |
12,2474487405 |
150,0000006518 |
0,0000000266 |
|
30 |
12,2474486008 |
12,2474487405 |
12,2474486707 |
149,9999989409 |
0,0000000432 |
|
… |
… |
… |
… |
… |
… |
|
40 |
12,2474487138 |
12,2474487139 |
12,2474487139 |
149,9999999985 |
0,0000000001 |
Построим график отклонения значения вычисленного корня от точного значения и построим линию тренда.

Рис. 2. Зависимость погрешности вычислений от количества итераций
Хорошо видно, что для достижения точность вычислений в 2–3 десятичных знака требуется около 16–18 итераций.
Перейдем к изучению вычисления значения квадратного корня в двоичной системе счисления. Немного истории. С появлением электронных вычислительных машин после возможности выполнения 4 арифметических операций появилась возможность вычисления квадратного корня. В первую очередь это было связано с тем, что вычисление корня в двоичной системе счисления довольно простое, и, что самое главное, была возможность аппаратной реализации вычисления. Поэтому на механической машине Готфрида Лейбница, работающей в двоичной системе счисления, была возможность вычисления квадратных корней. Да и первые калькуляторы могли выполнять 4 арифметических действия и вычислять квадратный корень. Все это было реализовано аппаратно. Это не единственный метод аппаратного вычисления корня [1, с. 3]. Но это классический алгоритм для понимания процесса вычислений. С развитием техники, увеличением скорости вычислений, появилась возможность делать это программно. Однако, методы не устаревают, а обретают новую форму. Перенесем алгоритм вычисления в двоичную систему счисления. Для понятности изложения примем, что число представлено с фиксированной запятой, имеющей по 8 бит для целой и дробной частей. Число 150 представим как 10010110.000000002. Так же, как и в выше описанном случае, выбираем интервал поиска корня. В данном случае на интервале 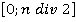 . В двоичной системе счисления это будет
. В двоичной системе счисления это будет 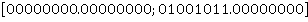 .
.
Таблица 2
Результаты вычисления 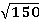 в двоичной системе счисления
в двоичной системе счисления
|
№ итерации |
a2 |
b2 |
c2 |
с22 |
с210 |
|
1 |
|
|
|
15010=10010110. 00000000002 |
75 |
|
2 |
00000000. 00000000 |
01001011. 00000000 |
00100101. 10000000 |
10101111110. 0100000000 |
37.5 |
|
3 |
00000000. 00000000 |
00100101. 10000000 |
00010010. 11000000 |
00101011111. 1001000000 |
18.75 |
|
4 |
00000000. 00000000 |
00010010. 11000000 |
00001001. 01100000 |
00001010111. 1110010000 |
9.375 |
|
5 |
00001001. 01100000 |
00010010. 11000000 |
00001110. 00010000 |
00011000101. 1100000100 |
14.0625 |
|
6 |
00001001. 01100000 |
00001110. 00010000 |
00001011. 10111000 |
00010001001. 0101010001 |
11.71875 |
|
7 |
00001011. 10111000 |
00001110. 00010000 |
00001100. 11100100 |
00010100110. 0010101100 |
12.890625 |
|
8 |
00001011. 10111000 |
00001100. 11100100 |
00001100. 01001110 |
00010010111. 0110011111 |
12.3046875 |
|
9 |
00001011. 10111000 |
00001100. 01001110 |
00001100. 00000011 |
00010010000. 0100100000 |
12.01171875 |
|
10 |
00001100. 00000011 |
00001100. 01001110 |
00001100. 00101000 |
00010010011. 1101001001 |
12.158203125 |
|
11 |
00001100. 00101000 |
00001100. 01001110 |
00001100. 00111011 |
00010010101. 1001010110 |
12.23046875 |
|
… |
… |
… |
… |
… |
… |
|
16 |
00001100. 00111110 |
00001100. 00111111 |
00001100. 00111111 |
00010010101. 1101111100 |
12.2421875 |
Точное значение корня 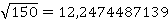 . Полученное значение с помощью бисекции
. Полученное значение с помощью бисекции 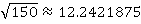 .
.
Аппаратно деление на 2 в двоичном коде осуществляется просто — сдвигом регистра, хранящего число, на 1 разряд вправо. Метод бисекции хорошо подходит для использования его в двоичной системе счисления. Метод содержит такие операции, как сложение, умножение, деление на 2 и возведение числа в квадрат. Все функции реализуются на аппаратном уровне. Следует заметить, что точность вычислений ограничена только разрядной сеткой вычислительной машины.
Погрешность составила 0,005, т. е. мы получили достоверность не более 2-х десятичных знаков. Связано это в первую очередь с 8-битным представлением десятичной части числа. Вес младшего разряда составляет 2–8=0,00390625. Значит, получить заданную точность можно только увеличив разрядную сетку.
Зависимость точности расчетов от разрядности машины при аппаратном решении задачи представлена в таблице 3.
Таблица 3
Зависимость точности расчетов от разрядности машины
|
Разрядность, бит |
Вес разряда |
|
8 |
0,00390625 |
|
16 |
1,52588*10–05 |
|
32 |
2,32831*10–10 |
|
64 |
5,42101*10–20 |
Ближе к практике лежит устройство поразрядного взвешивания. Алгоритм работы такого устройства следующий:
1. В старшем разряде rn устанавливается «1».
2. Число возводится в квадрат. Сверяется с введенным числом x.
3. Если число меньше, то в регистре оставляют «1», если больше — записывают «0».
4. Переходят к следующему разряду ri. Повторяют действия пунктов 2–4 до тех пор, пока не будет проверен последний разряд r0.
В результате результат достигается за n итераций, где n — количество разрядов.
В нашем случае понадобится 16 итераций для вычисления квадратного корня — итераций будет столько, сколько разрядов имеет разрядная сетка. Одно из таких устройств описано в [2, с.224]. Задачи вычислений, часто, критичны ко времени выполнения. Например, обработка сигналов в реальном времени. Для этого разрабатываются различные специализированные ИС (интегральные схемы). АЦП, ЦАП, имеющие в своей структуре устройства взвешивания. ИС, реализующие БПФ для обработки анализируемых сигналов. ПЛИС, позволяющие задать желаемую структуру цифрового устройства в виде принципиальной электрической схемы.
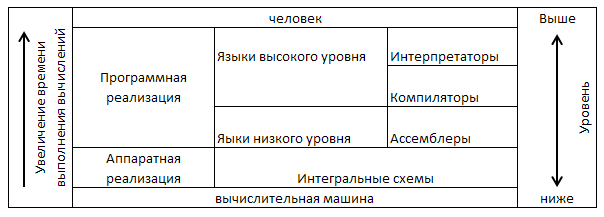
Рис. 3. Схема выбора реализации вычислений
Перед разработкой системы следует четко определиться с реализацией аппаратно-программного комплекса, решить, какие задачи будут решены с помощью аппаратной части, что — с помощью языков программирования.
Литература:
1. Патент RU 2005316 Российская Федерация, МПК G06F007/552. Устройство для возведения в квадрат и извлечения квадратного корня/ Олейников В. А.; заявитель и обладатель патента: Самарский государственный технический университет.
2. Карцев М. А. Арифметика цифровых машин. — Москва: Издательство «Наука», 1969. — 576 с.







