Многие производственные процессы как объекты управления характеризуются запаздыванием и априорной параметрической неопределенностью [1–12]. Построение систем управления для таких объектов весьма затруднительно, поскольку наличие запаздывания обычно порождает значительные проблемы. Кроме того, применение средств вычислительной техники приводит к тому, что цифровые алгоритмы управления в совокупности с непрерывными объектами делают замкнутые системы дискретно-непрерывными или гибридными [1–12].
В условиях априорной неопределенности задачу синтеза гибридной адаптивной системы управления (ГАСУ) с явной эталонной моделью для линейного объекта с запаздыванием по состоянию можно решить в рамках критерия гиперустойчивости [1, 2, 10], в соответствии с методикой, изложенной в работах [1, 10]. При этом, с целью расширения семейства алгоритмических структур контура адаптации, в процедуру синтеза систем управления вводится нелинейное преобразование фазовых координат [1, 9, 10]. Принципиальный момент, связанный с использованием нелинейных преобразований координат систем с последействием состоит в том, что способ их введения и обоснования отличается от ранее применяемых и носит, вообще говоря, хотя и строгий, но формальный характер. В частности, предлагаемый способ не позволяет для систем с любым типом запаздывания получить заранее гарантированный результат, например по повышению быстродействия контура адаптации. Однако, наряду с указанным недостатком, предлагаемый способ, во-первых, позволяет расширить класс возможных типов нелинейных преобразований фазовых координат, имеющих самостоятельное значение и, во-вторых, может представлять интерес для продолжения исследований в этой области, с целью получения новых теоретических результатов. Кроме того, в ряде случаев, что подтверждается и результатами имитационного моделирования [1, 3, 4, 10], с помощью нелинейных преобразований, удается существенно улучшить качественные показатели некоторых синтезированных систем адаптации.
Использование этого способа построения ГАСУ позволило синтезировать систему, основанную на следующей математической модели:
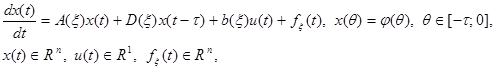 (1)
(1)
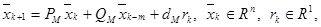 (2)
(2)
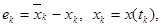
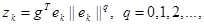 (3)
(3)
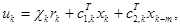 (4)
(4)
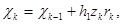
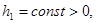 (5)
(5)
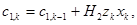
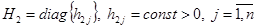 , (6)
, (6)
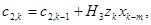
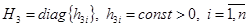 , (7)
, (7)
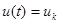 при
при 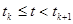 , (8)
, (8)
где x(t) — вектор состояния объекта управления; u(t) — управляющее воздействие; f(t) — возмущающее воздействие; A, D и b — матрицы и вектор соответствующего размера, числовые значения которых зависят от вектора неизвестных параметров 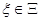 ;
; 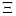 — известное множество возможных значений вектора
— известное множество возможных значений вектора 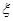 ;
; 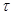 — время запаздывания;
— время запаздывания; 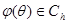 — начальная функция;
— начальная функция; 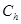 — пространство ограниченных непрерывных функций;
— пространство ограниченных непрерывных функций; 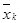 — вектор состояния эталонной модели; rk — задающее воздействие; PM, QM, dM — постоянные матрицы и вектор соответствующего размера; g — вектор, элементы которого подлежат выбору специальным образом;
— вектор состояния эталонной модели; rk — задающее воздействие; PM, QM, dM — постоянные матрицы и вектор соответствующего размера; g — вектор, элементы которого подлежат выбору специальным образом; 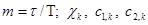 — настраиваемые коэффициенты регулятора;
— настраиваемые коэффициенты регулятора; 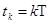 — дискретный аналог времени;
— дискретный аналог времени; 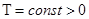 — шаг дискретизации; k = 0, 1, 2, … — номер шага.
— шаг дискретизации; k = 0, 1, 2, … — номер шага.
Поскольку алгоритмы настройки синтезированной ГАСУ разрабатывались в предположении затухающих возмущений f(t), то для построения контура самонастройки, работоспособного в условиях постоянного действия помех, подвергнем алгоритмы (5), (6), (7) огрублению:
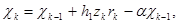
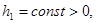
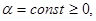 (9)
(9)
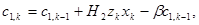 (10)
(10)
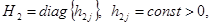
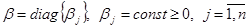 ,
,
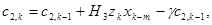 (11)
(11)
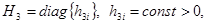
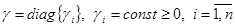 .
.
Применение робастных алгоритмов, образованных с помощью введения отрицательных обратных связей, имеет достаточно широкое применение. Однако недостатком этого способа регуляризации алгоритмов является существенное ухудшение процесса управления при значительном уменьшении модуля настраиваемых параметров. Преодолеть этот недостаток можно за счет включения и отключения обратных связей.
Рассмотренный способ построения робастных алгоритмов адаптации не является единственно возможным, еще один способ регуляризации алгоритмов самонастройки основан на введении в алгоритмы адаптации зоны нечувствительности.
Литература:
1. Еремин Е. Л., Еремина В. В., Семичевская Н. П., Шевко Д. Г. Алгоритмы и S-модели гибридных систем адаптивного управления. — Благовещенск, 2005. — 205 с.
2. Еремин Е. Л., Самохвалова С. Г., Шевко Д. Г. Адаптивные системы управления с настройкой компенсаторов. — Благовещенск, 2006. — 155 с.
3. Еремин Е. Л., Шевко Д. Г. Имитационное моделирование технически эквивалентных гибридных систем управления // Информатика и системы управления. — 2001. — № 2(02). — С. 36–42.
4. Еремин Е. Л., Шевко Д. Г. Синтез и упрощение технической реализации гибридной нелинейно преобразованной системы прямого адаптивного управления // Вычислительные технологии. — 2003. — Т. 8, № 3. — С. 47–57.
5. Еремин, Е.Л., Шевко, Д. Г. Методика синтеза гибридных нелинейно преобразованных систем прямого адаптивного управления на основе критерия гиперустойчивости // Вестник Амурского государственного университета. — 2003. — № 23. — С. 24–27.
6. Островерхий В. В., Шевко Д. Г. Задачи, решаемые автоматической системой управления шасси гусеничной машины // Вестник Амурского государственного университета. Серия: Естественные и экономические науки. — 2011. — № 53. — С. 69–73.
7. Самохвалова С. Г., Шевко Д. Г. Гибридная система адаптивного управления динамическим объектом с нестационарной матрицей выхода // Информатика и системы управления. — 2006. — № 2(12). — С. 138–144.
8. Шевко Д. Г. Гибридная система прямого адаптивного управления неминимально-фазовым объектом // Информатика и системы управления. — 2002. — № 1(03). — С. 112–120.
9. Шевко Д. Г. Критерий гиперустойчивости и синтез нелинейно-преобразованных гибридных систем прямого адаптивного управления // Вестник Амурского государственного университета. Серия: Естественные и экономические науки. — 2012. — № 57. — С. 65–69.
10. Шевко Д. Г. Модели и алгоритмы нелинейно преобразованных гибридных систем прямого адаптивного управления: дис. … канд. техн. наук. — Благовещенск, 2003.
11. Шевко Д. Г. Синтез алгоритмов самонастройки регулятора дискретной системы управления и сравнительный анализ качества процессов адаптации // Информатика и системы управления. — 2001. — № 1(01). — С. 97–105.
12. Шевко Д. Г. Синтез и нелинейные преобразования гибридных систем прямого адаптивного управления // Информатика и системы управления. 2002. № 2(04). С. 133–144.







