Одной из задач реформы высшего профессионального образования является подготовка высококвалифицированных специалистов, способных к профессиональному росту и профессиональной мобильности в условиях информатизации общества и развития новых наукоемких технологий. Основу профессиональной компетентности высококвалифицированных специалистов составляет предметная подготовка, в том числе и математическая, включающая в себя гибкость, критичность мышления, систематичность знаний, творческое саморазвитие. Высокий уровень математического развития способствует повышению уровня профессионализма. В связи со всем выше сказанным возникает необходимость повышения уровня качества обучения на фоне сокращения количества учебных часов на изучение математики в технических вузах.
Одним из способов повышения качества обучения математике является применение в образовательном процессе методов, направленных на становление и развитие познавательной активности и самостоятельности. Педагогическая технология развития критического мышления способствует активизации учебной деятельности, мотивации обучения и тем самым повышению его качества. С методической точки зрения данная технология — это система различных приемов, объединяющих все виды учебной деятельности, включающая модульное обучение, проблемное обучение, технологию учебной дискуссии и т. д.
Основу технологии развития критического мышления составляет модель трех стадий: «вызов — реализация (осмысление) — рефлексия (размышление)».
Первая стадия — стадия вызова. Основная цель данной стадии — актуализация имеющихся знаний об изучаемом предмете, обсуждение и запись всей информации, например, в виде верных и неверных утверждений. Применяются различные приемы такие как: графическая систематизация с помощью таблиц или кластеров, рассказ-предположение по ключевым словам, составление списка «известной информации» и т. д. Работа на данной стадии осуществляется как индивидуально, так и в группах. Все применяемые на стадии вызова приемы способствуют формированию познавательного интереса к предмету.
Вторая стадия — стадия осмысления. На данной стадии происходит первое знакомство с новой информацией, представленной либо в виде лекции, либо фильма, либо текста учебника. Далее происходит анализ новых знаний, соотнесение их ранее изученными и систематизация старых и новых знаний. Этому способствуют такие приемы как: ведение записей (двойные дневники, бортовые журналы), маркировка с использованием значков «+», «–»,«?», «v» («+» — то, что явилось интересным и неожиданным, «–» — то, что противоречит представлениям, «?» — то, о чем хотелось бы узнать подробнее, «v» — то, что уже известно), поиск ответов на поставленные в первой части вопросы и т. д. Учащиеся на стадии осмысления учатся формулировать умозаключения, делать выводы, работая индивидуально и в парах.
Третьей стадия — стадии рефлексии характерна творческая переработка, анализ, интерпретация и оценка изученной информации. На данной стадии первоначальные представления об изучаемом предмете переформировываются путем включения в них новых понятий. На этой стадии применяются такие методические приемы как: заполнение кластеров, таблиц, установление причинно-следственных связей между блоками информации; возврат к ключевым словам, логическим цепочкам, верным и неверным утверждениям; организация устных и письменных круглых столов и дискуссий; написание творческих работ; ответы на поставленные вопросы; исследования по отдельным вопросам темы и т. д. Возможны различные формы работы: фронтальная, групповая и индивидуальная.
Проиллюстрируем применение данной технологии на примере изучения дисциплины «Теория вероятностей и математическая статистика».
На первой лекции, на стадии вызова студентов можно разделить на группы, каждой из них дать текст, содержащий предложения, относящиеся к теме лекции «Предмет теории вероятностей и математической статистики. Основные понятия теории вероятностей» и попросить поставить около каждого предложения либо ложно, либо верно. А затем заполнить всем вместе таблицу (таблица 1) на доске и сообщить тему лекции.
Таблица 1
|
|
Теория вероятностей |
Ложно-верно |
|
1 |
Теория вероятностей — математическая наука, изучающая закономерности случайных явлений. |
|
|
2 |
Большой вклад в развитие теории вероятностей как науки внес Якоб Бернулли. |
|
|
3. |
В XIX– начале XX в. в. теория вероятностей становится отдельной математической наукой. |
|
|
4 |
Событие называется невозможным, если в результате испытания оно обязательно должно произойти. |
|
|
5 |
Событие называется достоверным, если в результате испытания оно вообще не может произойти. |
|
|
6 |
Вероятность достоверного события равна единице. |
|
|
7 |
Вероятность невозможного события равна нулю. |
|
|
8 |
Вероятность случайного события может быть отрицательной. |
|
На стадии осмысления группам предлагается текст лекции и дается задание заполнить «двухчастный дневник» (таблица 2).
Таблица 2
|
Основные этапы развития теории вероятностей/ Основные понятия теории вероятностей |
Определение |
|
|
|
На стадии размышления обсуждается и выносится на доску таблица 2. Далее возвращаемся к таблице 1, заполненной на стадии вызова, и каждый оценивает себя. В группах составляется кластер (рис.1) по теме лекции, который по мере изучения дисциплины постепенно заполняется, тем самым, способствуя систематизации знании по ней.
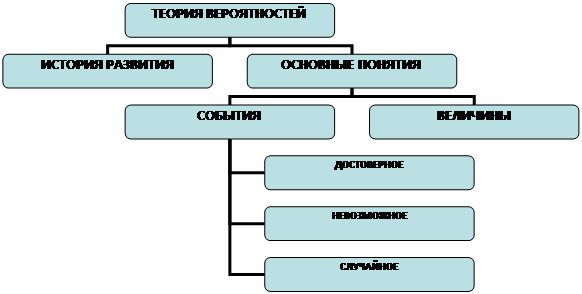
Рис. 1
Безусловно, активные методы обучения требуют много учебного времени, что может привести к невыполнению учебного плана и снижению качества образования. Но с другой стороны, на занятиях студенты активны, много работают самостоятельно, тем самым повышается мотивация обучения, а значит и эффективность занятий, учебный материал усваивается наиболее полно, постоянно растет мастерство педагога, а значит, повышается качество образования. При определенной подготовке преподаватель может организовать чередование занятий в активной и традиционной форме таким образом, чтобы выполнялся учебный план. Кроме того, повышение мотивации к обучению, происходящее при применении активных форм на занятиях, позволяет часть тем дисциплины предложить на самостоятельную проработку, активизируя тем самым самостоятельную работу.
Обучение в рамках данной технологии развития критического мышления способствует повышению мотивации обучения, студенты учатся самостоятельно строить умозаключения, логические цепочки доказательств, выражать свои мысли, свое собственное мнение, у них формируются качества мышления, характерные для математической деятельности, а затем и для профессиональной деятельности.
Литература:
1. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Профессиональная подготовка строителей через решение математических задач / Современные проблемы науки и образования. — 2014. — № 2. — С.168.
2. Куимова Е. И., Куимова К. А., Ячинова С. Н. Формирование мотивационной составляющей обучения на примере изучения дифференциальных уравнений / Молодой ученый. — 2014. — № 2(61). — С.775–777.
3. Куимова К. А., Куимова Е. И., Ячинова С. Н. К вопросу преподавания дисциплины «Спецглавы математики» / Молодой ученый. — 2014. — № 4. — С. 1011–1014.
4. Ячинова С. Н., Гудкова В. С. Мотивация обучения студентов посредством моделирования / Молодой ученый. — 2014. — № 4. — С.1141–1144.







