Составление дифференциального уравнения по условию задачи чаще всего состоит в определении математической зависимости между переменными величинами и их приращением [1]. Умение составить дифференциальное уравнение во многом зависит от навыка и понимания решающим физического содержания задачи.
Методика составления и решения дифференциального уравнения сводится к следующему:
- внимательному и подробному разбору условий задачи и выполнению чертежа;
- составлению соотношения между переменными и их приращениями для элементарного акта процесса (то есть процесса, протекающего за малый промежуток времени, или, в общем случае, в течение малого приращения аргумента);
- составлению дифференциального уравнения рассматриваемого процесса;
- интегрированию составленного дифференциального уравнения и определению его общего решения;
- исследованию общего решения;
- определению вспомогательных параметров (если они есть по условию задачи);
- выводу закона, определению частного решения дифференциального уравнения при заданных начальных условиях и числовому определению искомых величин (если это требуется по условию задачи);
- анализу ответа.
Составив соотношение между переменными величинами и их приращениями для элементарного акта процесса, переходят к пределу при стремлении приращения аргумента к нулю, получают дифференциальное уравнение в дифференциалах. Интегрирование полученного уравнения позволяет, объединив совокупность элементарных актов процесса, получить зависимость, которой подчиняется данный процесс в целом.
Иногда делается ряд допущений, упрощающих задачу, но не отражающихся в результатах. Например, бесконечно малые приращения величин заменяются их дифференциалами. Предполагается, что всякий физический процесс, рассматриваемый в течение бесконечно малого промежутка времени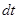 
, протекает с постоянной скоростью, и т. д.
Кроме того, при составлении дифференциального уравнения задачи, в зависимости от её условия, используются известные законы физики, химии, механики и других наук и различные математические сведения.
Обычно для заданных дифференциальных уравнений (или системы уравнений) определяются их решения (прямые задачи теории дифференциальных уравнений; в обратных задачах решения известны и требуется определить неизвестные структуру, порядок и параметры этого уравнений (или системы); эти задачи иначе называются задачами идентификации).
С точки зрения соотношения «причина-следствие» задачи математического моделирования условно разделяются на два больших класса: прямые задачи (известны причины, необходимо найти следствия) и обратные (известны следствия, нужно найти причины). Обычно обратными задачами называются задачи, решение которых состоит в определении причинно-следственных связей в рамках некоторой математической модели исследуемого объекта или процесса (определяются параметры данной модели по имеющимся результатам наблюдений и прочей экспериментальной информации).
Приведем простейший пример обратной задачи. Радиоактивный распад описывается физическим законом: скорость распада пропорциональна количеству радиоактивного вещества, имеющемуся в данный момент времени. Математической моделью этого процесса является решение задачи Коши для обыкновенного дифференциального уравнения
,
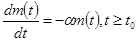где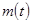 
— количество вещества в данный момент времени, 
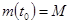- количество радиоактивного вещества в начальный момент времени, коэффициент пропорциональности 
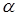- коэффициент распада. Если постоянные 
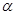и 
и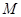звестны, то, решив задачу Коши, можно определить, как будет меняться количество радиоактивного вещества с течением времени. Обратная же задача заключается в определении коэффициента 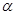и начальных данных 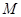по дополнительной информации о решени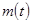и при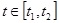 
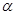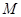(когда и неизвестны, но из эксперимента можно определить 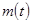для ).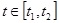
Далее рассмотрим ретроспективную идентификацию динамической системы, описываемой системой дифференциальных уравнений второго порядка. А именно, в результате эксперимента были определены осциллограммы колебаний технической системы по обобщенным координатам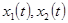 
и их скоростям 
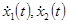при пробных воздействиях [2,3]. Требуется определить параметры технической системы в предположении, что ее поведение описывается системой дифференциальных уравнений вида:
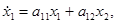
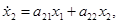
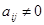(1)
или в векторно-матричной форме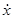 
=
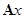, или
, 
.
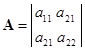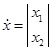Уравнения (1) определяют класс и структуру рассматриваемой технической системы. Таким образом, требуется определить параметры этой системы (коэффициенты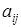 
уравнений (1)) по синхронным измерениям
,
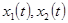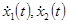
при «пробных воздействиях» (начальных условиях)
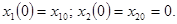(2)
Характеристическое уравнение системы (1) имеет вид
,
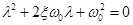а корни этого уравнения есть
,
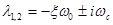где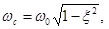 
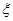- соответственно собственная частота и относительный коэффициент демпфирования 
.
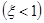Справедливо:
;
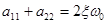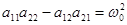. (3)
Введя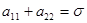 
=
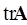(след матрицы) и 
=
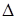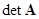, (3) можно представить в виде
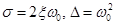. (4)
Откуда
.
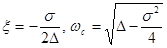Решение системы (1), удовлетворяющее начальным условиям (2), имеет вид:
;
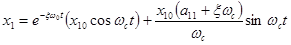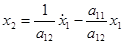. (5)
По осциллограмме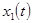 
легко определить 
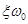и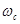 
, откуда
.
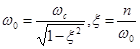Отметим, что кривая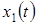 
соответствует реальному процессу, происходящему в рассматриваемой технической системе, то есть является реакцией системы по координате 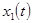при пробных воздействиях (2). А 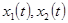, определяемые по (5), являются лишь приближением — моделями процессов 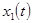и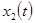 
в выбранном классе, определяемом видом системы (1).
Из (1) имеем
;
.
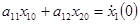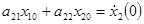С учетом (2), (4) получим:
; 
; 
; 
.
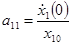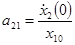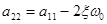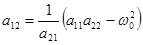Таким образом, при известной структуре системы дифференциальных уравнений по заданному ее решению при начальных условиях
, 
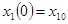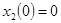
определили неизвестные параметры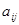 
технической системы. Отметим, что при этом кроме 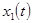и 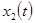для определения 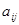потребовались и синхронные реализации 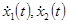(во всяком случае, в окрестности 
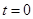). Рассмотренная задача — есть частная задача параметрической идентификации или частная задача идентификации. Если бы вид систем уравнений, решением которой являются экспериментальные процессы 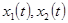, был неизвестен, то задача значительно усложнилась бы (это общая задача идентификации).
Как видим, в отличие от задач прямого моделирования обратные задачи относятся к классу «некорректных» (в математическом смысле), в частности неустойчивых относительно погрешностей входных данных. Для корректности постановки задачи необходимо:
- существование решения при всех допустимых исходных данных;
- единственность данного решения;
- устойчивость решения к изменениям (малым) исходных данных.
Если задача не удовлетворяют хотя бы одному из указанных условий, то она называется некорректно поставленной.
Некорректность присуща обратным задачам почти всегда; в одних случаях она может быть преодолена весьма просто, в других вообще требует переосмысления понятия самого решения
Из указанного следует, если при приближенном решении обратной задачи использовать какой-либо классический алгоритм формально без учета некорректности задач, то возможно получение результата, не имеющего ни научной, ни прикладной ценности. Игнорировать некорректность постановки задачи нельзя. Для ее преодоления имеются два пути:
- корректная постановка задачи, основанная на привлечении дополнительной информации об искомом решении;
- управление классическими алгоритмами некорректно поставленной задачи.
При идентификации рассмотренной выше системы второго порядка использовалась дополнительная информация об искомом решении: результаты экспериментальных исследований практически совпали с теоретическим решением системы (1) при заданных начальных условиях [4].
Литература:
1. Данилов А. М. Данилов А. М., Фадеева Г. Д. Дифференциальные уравнения. — Пенза: ПГАСА. — 1997. — 144 с.
2. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС. — 2011. — 296 с.
3. Данилов А. М., Гарькина И. А. Интерполяция, аппроксимация, оптимизация: анализ и синтез сложных систем: монография. — Пенза: ПГУАС. –2014. — 168 с.
4. Математические методы в строительном материаловедении: монография / И. А. Гарькина [и др.]; под ред. акад. РААСН В. И. Соломатова. — Саратов: Изд-во Сарат. ун-та. — 2001. — 188 с.
