Эта серия задач направлена на выявление некоторых особенностей умственного восприятия школьниками математической задачи. Переопределенные задачи позволяют выявить, как учащиеся из совокупности данных им величин выделяют именно те, которые представляют собой систему отношений, составляющих существо задачи, и являются необходимыми и достаточными для ее решения. Столкнувшись с такой задачей, ученик должен выделить минимальное количество данных, необходимое для решения, и объяснить, почему другие данные излишни.
Задачи переопределённые — задачи с избыточным составом условия, с лишними данными, без которых ответ может быть получен, но которые в той или иной мере маскируют путь решения. Данные в таких задачах могут быть противоречивыми и выявление этой противоречивости или непротиворечивости является обязательным элементом решения такой задачи.
Например, в задаче «Найти площадь прямоугольного треугольника с катетами 9 СМ и 40 СМ и гипотенузой 41 СМ» мало найти ответ полупроизведением 9 на 40. Надо ещё выявить, будет ли у прямоугольного треугольника с катетами 9 СМ и 40 СМ гипотенуза равной 41 СМ. Без этого выяснения решение задачи не может быть признано полным. В этом аспекте интерес представляют практические задачи. Например, при изучении первой формулы площади треугольника учитель приносит в класс вырезанный из бумаги треугольник с проведенными высотами и предлагает одному из учащихся измерить длину какой — либо стороны, потом второму ученику длину второй стороны, третьему — третьей, ещё трое измеряют высоты, каждый по одной. Результаты измерений записываются на доске. Теперь учитель предлагает вычислить площадь этого треугольника.
Вопрос, какая высота к какой стороне проведена, учитель переадресует учащимся, которые измеряли, но те, естественно, не помнят, поскольку не фиксировали на этом внимания. Возникает интересная проблема, которая в итоге всё же разрешается, исходя из того, что площадь одного и того же треугольника не может иметь разных значений. Поэтому самая большая высота должна быть проведена к самой маленькой стороне, а самая маленькая к самой большой. Теперь площадь треугольника можно вычислять тремя способами, но результат, как выясняется, получается не совсем одинаковым.
Появляется причина поговорить о сущности измерений, об их обязательной неточности, о качестве приближённых измерений, об особенностях вычислений с приближёнными числами и других соответствующих вопросах. И элементарная задача на применение примитивной формулы наполняется богатым содержанием.
Задачи этого типа требуют от ученика умения анализировать условие, находить в нём нужные данные и отбрасывать ненужные. Причём, «ненужными» у разных учеников могут быть разные величины. Отсюда можно получить и один из надёжных способов самоконтроля в решении традиционных задач: после получения ответа вставить этот ответ в текст задачи как одно из данных, а одну из известных величин считать неизвестной и решить полученную новую задачу.
Приведем примеры такого рода задач(избыточные данные выделены курсивом):
1. В магазине развесили картофель в 24 пакета весом по 3 и 5 кг, причем число первых оказалось больше, чем вторых. Вес всех пятикилограммовых пакетов оказался равным весу всех трехкилограммовых пакетов. Сколько было тех и других?
2. На автостоянке находятся 40 машин—автомобили и мотороллеры. У них вместе 100 колес и 40 рулей. Сколько тех и других машин?
3. У мальчика было несколько копеек. Когда ему дали еще 14 коп., то он на все деньги купил 4 карандаша, заплатив за каждый вдвое больше того, что он имел прежде. На свои прежние деньги он не мог купить и одного карандаша. Сколько денег было у мальчика до получения 14 коп.?
4. Четыре гири весят вместе 40 кг. Определить вес самой тяжелой гири, если известно, что каждая из них в 3 раза тяжелее другой, более легкой, и что самая легкая весит в 12 раз меньше, чем весят вместе две средние.
5. Из города А в город В вышел поезд со скоростью 48 км в час. Двумя часами позже за ним вышел второй поезд со скоростью 56 км в час. На каком расстоянии от отправного пункта второй поезд нагонит первый, если расстояние между городами 1200 км, а в первом поезде вдвое больше вагонов, чем во втором?
6. Точки А, В, С лежат на окружности с центром в точке О, ÐАВС = 50°, ÈАВ:ÈСВ = 5:8. Найти ÐАОС.
Рассмотрим методику работы с задачей, содержащей лишнее данное, на примере последней задачи.
I. Осмысление условия.
В: Какая геометрическая фигура нам дана?
О: Окружность.
В: Что сказано о точках А, В, С?
О: Они принадлежат окружности.
В: Какие величины нам известны в задаче?
О: ÐАВС=50°, ÈАВ:ÈСВ = 5:8.
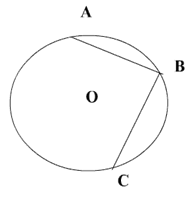
Запишем условие задачи:
Дано: (О, г) А,В,С Є (О, г)
ÐАВС= 50°,ÈАВ:ÈСВ=5:8
Найти: ÐАОС
II. Поиск пути решения.
В: Что нужно найти?
О: ÐАОС
В: Каким углом является ÐАВС?
О: Вписанным углом.
В: Каким углом является ÐАОС?
О: Центральным углом.
В: Что общего у этих углов?
О: Они опираются на одну дугу.
В: Что можно сказать о ÈАС если ÐАВС=50°?
О: ÈАС будет в два раза больше чем ÐАВС.
В: Сможем ли мы найти ÐАОС, зная длину дуги, на которую он опирается?
О: Да, он равен длине этой дуги.
В: Все ли данные задачи мы использовали?
О: Нет, еще есть отношение ÈАВ:ÈСВ = 5:8.
В: Получим ли мы ответ, не используя это отношение?
О: Да.
В: Каким данным является ÈАВ:ÈСВ = 5:8?
О: Лишним, в решении задачи мы его не используем.
Убедимся в этом, реализуя наш план решения.
III. Реализация плана решения.
ÐАВС — вписанный, опирается на ÈАС. Значит ÐАВС=½ ÈАС Þ ÈАС= 2ÐАВС. ÈАС = 100°.
ÐАОС — центральный, опирается на ÈАС. Значит ÐАОС= ÈАС Þ ÐАОС = 100°.
Убедились, что отношение ÈАВ:ÈСВ = 5:8 являлось избыточным данным в задаче.
Из выше сказанного видно, что данный тип задач несёт в себе определённую развивающую функцию, а именно, переопределённые задачи требуют умения анализировать условие и строить решение задачи при помощи минимального числа данных, что несомненно важно для изучения математики.
Литература:
1. Акимова И. В., Буркина В. А., Титова Е. И. Моделирование задач с аномальным условием и методика пути поиска их решения // Современные проблемы науки и образования. — № 1, 2014г.
2. Буркина В. А., Титова Е. И. Методика работы с аномальными задачами// Молодой ученый. 2014. № 2 (61). С. 740–741.
3. Гребенев И. В., Ермолаева Е. И., Круглова С. С. Математическая подготовка абитуриентов — основа получения профессионального образования в университете // Наука и школа. 2012. № 6. С. 27–30.
4. Жидкова А. Е., Титова Е. И. Изучение школьной математики как пропедевтический курс ее обучения в техническом вузе// Современные проблемы науки и образования. 2013. № 6.
5. Титова Е. И., Чапрасова А. В. Различные трактовки понятия «задача» и методика их решения// Молодой ученый. 2014. № 6 (65). С. 760–762.
6. Титова Е. И., Романкова А. А. Неопределенные задачи в школьном курсе математики// Вестник магистратуры. 2014. № 6–1 (33). С. 128–129.







