Анализ несущей способности лестничного марша при нагрузках, не предусмотренных проектом

Жилищная застройка в России развивается все большими темпами, при этом множество зданий выполняются по бескаркасной схеме с наружными и внутренними несущими стенами. Кладка несущих стен здания в пределах лестничной клетки выполняется способом, когда подмости устанавливаются одной половиной на лестничный марш, а другой — на лестничную площадку, при этом на подмости устанавливается поддон с кирпичем, тогда как в типовых сериях на лестничные марши таковой нагрузки не предусмотрено. Данное обстоятельство может привести к обрушению лестничного марша и его падению на нижележащие конструкции, что подтверждается примерами из практики.

Целью настоящего исследования является расчет прочности и максимальной несущей способности железобетонного лестничного марша выполненного по серии 1.151.1–6 «Марши лестничные, железобетонные плоские для жилых зданий высотой 2,8 м, вып.1».

Исследуемый марш был изготовлен по серии 1.151.1–6 «Марши лестничные, железобетонные плоские для жилых зданий высотой 2,8 м, вып.1. Марши шириной 105 см и 120 см с бетонной поверхностью без фризовых ступеней»; марка марша 1ЛМ 27.12.14–4. Изготовление марша предусмотрено из тяжелого бетона марки по прочности на сжатие для 5-ти этажного дома М 300 (В 20). При изготовлении маршей должно быть обеспечено проектное положение рабочей арматуры согласно ГОСТ 9818.0–81 и по ГОСТ 13015.1–80. Опирание лестничного марша сверху должно быть 70 мм, а снизу — 64 мм. Для марки 1ЛМ 27.12.14–4 имеем расчетную нагрузку равную 1012 кгс/м.

Подобный лестничный марш был смонтирован на жилом здании, после установки на него подмостей и поддона кирпича наполненностью 50 % и нахождении на нем двух человек произошло обрушение лестничного марша и падение его на нижележащий марш, что привело к обрушению последнего и повлекло за собой травмы людей.

Для расчета несущей способности определим действующие нагрузки на лестничный марш:

1.                  Вес поддона для кирпича в соответствие ГОСТ 18343–80–35 кг

2.                  В поддоне находилось 300 кирпичей массой одного кирпича 4,8 кг по ГОСТ 379–95, что в сумме составляем 1440 кг, а с учетом веса поддона составит 1475 кг.

3.                  В соответствие с СП 20.13330.2011 «Нагрузки и воздействия» вес одного человека принимается равным 75 кг [1].

4.                  В соответствие с замерами общий вес подмостей составляет 255 кг.

5.                  Собственный вес железобетонного марша составляет в соответствии с серией (Серия 1.151.1–6) — 1520 кг.

Расчетная схема лестничного марша представлена на рис.1

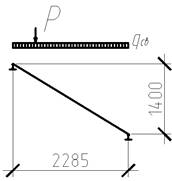
Рис. 1. Расчетная схема лестничного марша, где Р — сила, передающаяся на лестничный марш от массы подмостей, двух человек и поддона с кирпичом, q_св — собственный вес лестничного марша

 

По таблице 4 (Серия 1.151.1–6) на листе 8 имеем величину контрольной нагрузки при проверке трещиностойкости, равную 1025 кгс/м, тогда нормативная нагрузка равна:

1025–383=642 кгс/м,

где 383 кгс/м — дополнительная нагрузка при образовании трещин (лист 8, табл.4 серии Серия 1.151.1–6).

Расчетная погонная нагрузка от собственного веса составит:

q=642х1,1=706 кгс/м

Коэффициент 1,1 принят в соответствие с таблицей 7.1 СП 20.13330.2011 «Нагрузки и воздействия» [1]. Для определения силы Р, действующей сосредоточено, сложим следующие величины:

G_ч=75х1,2=90 кгс — расчетная нагрузка от веса одного человека

G_п=255 кгс — собственный вес подмостей

G_к=1475х1,1=1622,5 кгс — собственный вес кирпича с учетом веса поддона.

Коэффициент 1,1 принят в соответствие с таблицей 7.1 СП 20.13330.2011 «Нагрузки и воздействия». Тогда общий вес всех элементов будет составлять:

G= 255+90х2+1622,5=2058,5 кгс

Так как в подмостях имеется две опоры, то вес будет распределяться на обе опоры. Как наиболее невыгодный вариант примем тот, в котором кирпич и каменщики стояли непосредственно над опорой, передающей нагрузку на лестничный марш, при этом нагрузка от подмостей будет учтена как половина их веса. Тогда суммарная сила Р будет равна:

Р=G-G_п/2=2058,5-255/2=1931 кгс.

Для удобства расчета перейдем к балочной расчетной схеме, где длина балки соответствует длине марша; схема расположения нагрузки принята соответственно схеме загружения марша:

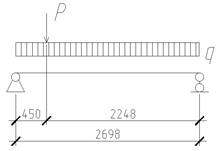
Рис. 2. Расчетная схема плиты марша

 

Найдем опорную реакцию от силы Р:

R=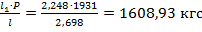

Найдем изгибающий момент в марше от опорной реакции:

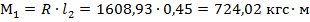
Найдем изгибающий момент в марше от собственного веса:

М₂=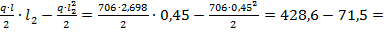

=

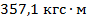
Общий момент, воспринимаемый сечением марша в момент разрушения, равен:

М=М₁+М₂=724,02+357,1=1081,12 кгс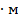

Определяем изгибающий момент в месте разлома лестничного марша, то есть в середине его длины. Максимальный изгибающий момент от собственного веса составит:

М_max=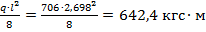

Найдем опорную реакцию от силы Р:

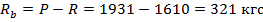
Изгибающий момент в середине марша от силы Р составит:

М₁=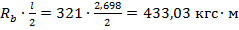

Общий изгибающий момент в середине сечения марша составит:

М= М_max+ М₁=642,4+433,03=1075,43 кгс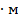

Данный момент несколько меньше момента в месте приложения силы Р? поэтому для дальнейших расчетов принимаем момент в размере 1081,12 кгс.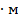

Проведем расчет максимальной несущей способности марша на общий изгибающий момент.

Коэффициент:

где М — изгибающий момент в сечении марша, R_b= 11,5 МПа- прочность бетона на сжатие [2, табл. 6.8], b — ширина лестничного марша (Серия 1.151.1–6), h_0 — высота рабочей зоны бетона (рассчитывается как высота плиты лестничного марша (Серия 1.151.1–6 (лист 12, разрез 3–3, равно 122 мм) за вычетом защитного слоя бетона (в соответствии с замерами 36 мм).

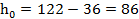 мм

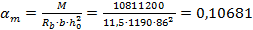
Соответствующие значения: ξ=0,111; v=0,944 [2]. Поскольку ξ=0,11< ξ_R=0,627 [2], то максимальный изгибающий момент, который способен выдержать марш, равен:

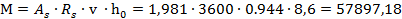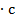 кгсм

(579 кгсм)

где М — изгибающий момент в сечении марша, A_s- площадь поперечного сечения семи стержней (площадь семи стержня равна 0,283см²х7=1,981 см²); R_s=3600 кгс/см² _— прочность арматуры на растяжение [2, табл. 6.14].

При сравнении полученных данных видно что, максимальный изгибающий момент, воспринимаемый сечением, в 1081,12/579=1,867 раза меньше момента, воздействующего на лестничный марш.

Если принять в расчете не расчетное сопротивление арматуры по площадке текучести, а по временному сопротивлению (предшествующему разрушению) равному 6000 кгс/см² [2],то будем иметь:

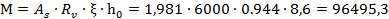 кгс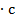м = 964,95 кгсм

Таким образом, можно сделать вывод о том что, лестничный марш во время монтажа каменной кладки с подмости, на которой находились поддон кирпича весом 1475 кгс и два каменщика, был нагружен сверх нормативного значения как минимум в 1081,12/964,95=1,12 раза, что и привело к обрушению лестничного марша.

Так как при освидетельствовании лестничного марша были выявлены отступления от проектных размеров (увеличение толщины защитного слоя с 15 до 36 мм), произведем перерасчет несущей способности лестничного марша с проектным защитным слоем:

Коэффициент: ;

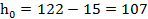 мм

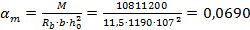
Соответствующие значения: ξ=0,072; v=0,959 [2]. Поскольку ξ=0,072< ξ_R=0,627 [2], то максимальный изгибающий момент, который способен выдержать марш, равен:

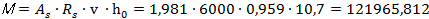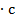 кгсм

(1219,65 кгсм)

Таким образом, можно сделать вывод о том, что при соблюдении на производстве проектных размеров лестничного марша (а именно, величины защитного слоя) обрушения последнего можно было избежать.

Произведем расчет марша ведущего с площадки между первым и вторым этажом на второй этаж при падении на него обрушавшегося марша третьего этажа. В качестве нагрузки примем общий вес марша в размере 1520 кг и приложим ее в качестве сосредоточенной нагрузки на центр марша [3]. Расчет ведем по схеме когда балка воспринимает изгибающий удар, расчетная схема представлена на рис. 3.

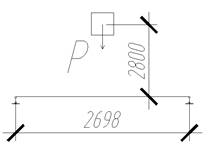
Рис. 3. Расчетная схема марша при падении на него груза

 

Вычислим стрелу прогиба балки:

0,139 см,

где Р — нагрузка от собственного веса марша в размере 1520 кгс, l- длина лестничного марша в размере 269,8 см, Е- модуль упругости бетона равный 245000 кгс/см² [2], J — момент инерции лестничного марша, b-ширина лестничного марша равная 119 см, h-высота плиты лестничного марша равная 12,2 см. Вычислим коэффициент динамичности:

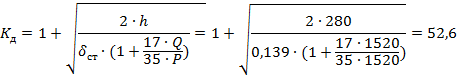
где h- высота падения марша принятая равной 280 см, 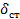- стрела прогиба балки.

Вычислим динамический прогиб:

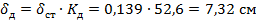
Вычисляем динамический момент, который воспринимает сечение:

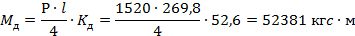
где Р — нагрузка от собственного веса марша в размере 1520 кгс, l — длина лестничного марша в размере 269,8 см, К_д — коэффициент динамичности равный 52,6.

Так как значение 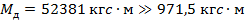, делаем заключение о том, что при падении лестничного марша с высоты 2,8 м на другой лестничный марш он должен разрушиться, что и произошло в действительности.

Выводы:

-          В соответствие с данными расчета несущей способности плиты лестничного марша можно сделать вывод о том, что разрушение лестничного марша произошло вследствие превышения расчетной нагрузки на марш и его недостаточной несущей способности в момент разрушения.

-          Расчетная нагрузка на марш в момент разрушения, помимо собственного веса в размере 706 кгс/м, составила 1932,15 кгс и являлась сосредоточенной нагрузкой. При этом максимальный изгибающий момент в 1081,6/971,5=1,106 раза больше чем момент, который может воспринять сечение.

-          Разрушение лестничного марша ведущего с площадки между первым и вторым этажом на второй этаж произошло вследствие динамического удара разрушившегося марша вышележащего этажа с находящейся на нем нагрузкой от поддона с кирпичом и собственного веса фрагментов лестничного марша.

 

Литература:+

 

1.         СП 20.13330.2011 Нагрузки и воздействия. Актуализированная редакция СНиП 2.01.07–85*. М., 2011. 80 с.

2.         СП 63.13330.2012. Свод правил. Бетонные и железобетонные конструкции. Основные положения. Актуализированная редакция СНиП 52–01–2003. М., 2013.

3.         Справочник по сопротивлению материалов/ С. П. Фесик — 2-е изд., перераб. и доп. — Киев: Будивельник, 1982. — 280 с.