При оценке акционерной стоимости компании (АК), помимо основных активов (здания, сооружения, машины, оборудование) и оборотных (сырье, материалы, топливо, энергия) активов (SOF), огромное значение приобретают нематериальные активы, которые трудно поддаются оценке традиционными методами. Это интеллектуальный капитал организации (IK, ИК).
Рыночная стоимость компании реагирует также на действие ряда нерыночных факторов - административных, политических, социальных, географических, судебных и других случайных воздействий.
В общем случае акционерная стоимость компании в момент времени i определяется соотношением:
AKi = IKi + SOFi + SSi. (1)
В (1) SS означает влияние случайных факторов. Индекс i характеризует дискретный момент времени, в который осуществляется оценка.
Соотношение (1) позволяет выделить и оценить величину интеллектуального капитала организации. Оценка интеллектуального капитала фирмы необходима по ряду причин:
- он выступает в качестве важнейшей компоненты, определяющей конкурентоспособность организации;
- увеличивает рыночную капитализацию;
- свидетельствует о степени развития организации.
Акционерная стоимость компании в каждый момент i легко наблюдается и рассчитывается по текущей стоимости акций.
Стоимость основных и оборотных средств является учетной и легко прогнозируется по нормативам морального и материального износа, графику передвижения материальных ресурсов, то есть
SOF(t) = SOFi . (2)
Если составляющая SSi не имеет ненулевого тренда, то ее среднее значение на некотором промежутке времени равно нулю. Это позволяет упростить соотношение (1), выполнив расчеты левой части по формуле:
AK(t) = ∑ AK(i) (3)
операцию скользящего среднего для каждого момента времени t в течении предшествующего промежутка Δ t. В этом случае получим:
AK(t) = IK(t) + SOF(t). (4)
Влияние случайных факторов, таким образом, исключено. Промежуток Δ t должен быть с одной стороны достаточно большим, чтобы среднее значение случайной величины было гарантировано равно нулю, и, одновременно достаточно малым, чтобы не «усреднить» тенденции изменения иных переменных (1).
Величина Δ t определяется эмпирическим путем и с использованием имеющейся у лица, принимающего решение (ЛПР), априорной информации об исследуемом процессе.
Если составляющая SSi имеет ненулевой тренд, то его следует дополнительно идентифицировать.
Из (4) следует формула для определения интеллектуального капитала организации:
IK(t) = AK(t) - SOF(t). (5)
Ряд (5) характеризует динамику изменения интеллектуального капитала компании. Он позволяет построить модель авторегрессии (6), с помощью которой можно прогнозировать развитие интеллектуального потенциала без учета внешних воздействий /1/. Модель (6) в качестве исследуемой зависимости использует универсальную переменную у(t), так как она может означать и AK(t) и IK(t).
у(t) = а1у(t-1) + а2у(t-2)+ … + аnу(t-n). (6)
Модель (6) учитывает внутреннюю логику изменения интеллектуального потенциала компании, определяемую ее структурой, корпоративной культурой, стилем управления руководителей. Параметр модели n характеризует инерционность процесса преобразования интеллектуального капитала в компании: результаты обучения сотрудников, также как и «старение» ИК проявляются не мгновенно. Коэффициенты аj определяют степень влияния момента измерения фактора. Чем ранее наблюдался фактор, тем менее влияет он на результат. Неизвестные коэффициенты модели легко определяются статистическими методами на основе эмпирических наблюдений /1/.
Этот прогноз, транслируемый на заданное число шагов (для прогноза значения ИК в момент времени t+2 в правой части используется прогноз значения предыдущего момента и т.д.), дает представление о будущем компании и позволяет определить момент и характер управляющих воздействий. Такими воздействиями, изменяющими ИК организации, могут служить следующие действия менеджмента организации: приобретение интеллектуальной собственности, разработка инноваций, изменение параметров организации, приглашение новых сотрудников и т.д.
Рассмотрим механизм идентификации неизвестных параметров модели (6) по эмпирическим наблюдениям, заданным таблицей 1. Для простоты рассуждений используем простую модель, учитывающую два такта предыстории. То есть идентифицируем модель вида:
у(t) = а1у(t-1) + а2у(t-2). (7)
Запишем эту модель относительно данных, сдвинутых на один такт:
у(t-1) = а1у(t-2) + а2у(t-3). (8)
Таблица 1. – Форма представления результатов наблюдений и расчетов
|
i, t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
∑ |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
y2(t) |
|
|
|
|
|
|
|
|
|
|
с1 |
|
у(t)у(t-1) |
- |
|
|
|
|
|
|
|
|
|
с2, в11 |
|
у(t)у(t-2) |
- |
- |
|
|
|
|
|
|
|
|
в12, в21 |
|
у(t)у(t-3) |
- |
- |
- |
|
|
|
|
|
|
|
в22 |
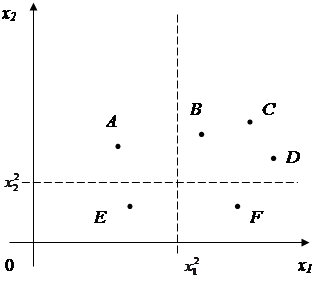
Рис. 1. – Графическая иллюстрация процедуры скользящего среднего
Соотношения (7) и (8) представляют собой систему двух уравнений с двумя неизвестными а1 иа2, но коэффициенты этой системы заданы с ошибкой. Чтобы компенсировать влияние ошибки на решение умножим обе части (7) и (8) на у(t) и просуммируем по переменной t. Результаты расчетов сведены в таблицу 1. Решаемая система линейных алгебраических переменных имеет вид:
∑ y2(t) = а1∑ у(t)у(t-1) + а2∑ у(t)у(t-2),
∑ у(t)у(t-1) = а1 ∑ у(t)у(t-2) + а2∑ у(t)у(t-3),
или
с1 = а1в11 + а2в12
с2 = а1 в12 + а2в22,
в которой суммирование осуществляется по t. Порядок расчетов очевиден из таблицы 1. Обозначено:
с1 =∑ y2(t), с2= в11=∑ у(t)у(t-1), в12= в12=∑ у(t)у(t-2), в22=∑ у(t)у(t-3).
Следующим шагом совершенствования методики оценки интеллектуального капитала компании является включение в модель управляющих факторов. Для случая воздействия на ИК одним управляющим фактором u(t) модель имеет вид:
у(t) = а1у(t-1)+а2у(t-2)+…+ аnу(t-n)+ u(t)+в1 u(t-1)+в2 u(t-2)+…+ вmи(t-m). (6)
В данном соотношении параметр m также отражает инерционность, но теперь уже влияния управляющего воздействия. Коэффициенты вk оценивают изменение значимости управлений от времени.
Если управляющих воздействий несколько модель расширяется аналогично.
Литература:
1. Ротштейн А.П. Нечеткий многокритериальный выбор альтернатив: метод наихудшего случая // Теория и системы управления, 2009, № 3.
2. Bellman R., Zadeh L. Decision Making in Fuzzy Environment // Management Science. 1970. V. 17.
3. Саати Т. Математические методы конфликтных ситуаций. М.: Сов. Радио, 1977.
4. Борисов А.Н., Крумберг О.А., Федоров И.П. Принятие решений на основе нечетких моделей: Примеры использования. Рига: Зинатне, 1990.
5. Саати Т., Кернс К. Аналитическое планирование. Организация систем. М.: Радио и связь, 1991.
6. Rotshtein A.P. Modification of the Saaty Method for the Construction of Fuzzy Set Membership Functions // Proc. Inf. Cont. on Fuzzy Logic and Its Application. Israel, 1997.
7. Ротштейн А.П., Штовба С.Д. Нечеткий многокритериальный анализ вариантов с применением парных сравнений // Изв. РАН ТиСУ. 2001. №3. С. 150-154.
8. Нечипоренко В.И. Структурный анализ систем: надежность и эффективность. М.: Сов. радио, 1976.







