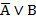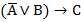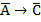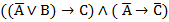Решение логической задачи разными способами и сравнение их эффективности

Статья посвящена обзору различных способов решения логических задач и сравнению их эффективности. Логические задачи можно решать различными способами. У каждого из них есть свои достоинства и недостатки. Поэтому для решения подобного типа задач нужно найти такой способ, который имеет наименьшее количество недостатков, а следовательно, дает уверенность в правильности решения.

Ключевые слова: логика, логическая задача, алгебра логики, метод таблиц, метод рассуждений.

Abstract. This article is dedicated to various methods of solving logic exercises and comparing their effectiveness. Logic exercises can be solved by different methods. Each method has its own pros and cons. That’s why for solving logic exercises it’s necessary to find such method, that’s has she least number of cons.

Keywords: logic, logical exercise, the algebra of logic, method tables, method of reasoning.

На протяжении всех лет обучения в школе, начиная с начальных классов, мы решаем множество задач, в том числе и логических. Для успешного решения такого типа задач нужно: научиться выделять их общие признаки, выдвигать различные гипотезы, подмечать закономерности, строить цепочки рассуждений, проверять их на истинность, делать выводы. Существуют разные способы решения логических задач. К ним относят: применение законов алгебры логики, табличный способ, использование рассуждений [4, с. 223].

У каждого способа есть свои достоинства и недостатки. Поэтому для нахождения наиболее эффективного из них, в зависимости от задачных ситуаций, рассмотрим решение задач разными способами и проанализируем эти решения. Под эффективностью понимается большее количество преимуществ решения.

Традиционно к логическим задачам относят задачи на соответствия между множествами [5, с. 67].

Задача 1.Три девочки были в белом, красном и голубом платьях. Их туфли были тех же трёх цветов.

1. Только у Тамары цвет платья и туфель совпали.

2. Валя была в белых туфлях.

3. Ни платье, ни туфли Лиды не были красными.

Определите цвет платья и туфель каждой из девочек [3, с. 197].

Решение.

I способ. С помощью совмещенной таблицы.

Данная задача трехмерная, следовательно, нужно найти соответствия между множествами (имена и туфли, имена и платья, платья и туфли). Для этого используют 3 таблицы, которые затем совмещаются. Таблица заполняется из условий. Знак «+» ставится тогда, когда выясняется точное соответствие между элементами множеств, знак «-» ставится тогда, когда выясняется несоответствие. Если в какой-то строке малой таблицы получается два знака «-», то в третьей нужно поставить знак «+». Из условия 2 в таблице ставится знак «+» на пересечении графа «Валя» и «Белые туфли». Также из условия 2 получается, что Валя была в белых туфлях, а туфли Лиды не были красными, следовательно, Лида была в голубых туфлях, а Тамара в красных. У Тамары цвет туфель и платья совпали по условию 1, а у двух других девочек нет, следовательно, у Вали было голубое платье, а у Лиды белое.

Таблица 1

Таблица соответствия имен и одежды

Ответ: Тамара – красные туфли, красное платье; Валя – белые туфли, голубое платье; Лида – голубые туфли, белое платье.

IIспособ. С помощью рассуждений.

По условиям задачи туфли Лиды не были красными, а у Вали были белые туфли, значит, красные туфли были у Тамары, а Лиды голубые. Так как у Тамары цвет платья и туфель совпали, то платье у Тамары было красное. У Вали и Лиды цвета не совпадали, значит у Вали было голубое платье, а у Лиды белое.

Ответ: Тамара – красные туфли, красное платье; Валя – белые туфли, голубое платье; Лида – голубые туфли, белое платье.

Оба выше приведенных способа дают результат при решении данной задачи. Решение с помощью таблицы дает наглядность и логичность, что способствует уверенности в правильности ответа, но занимает большое количество времени. Решение с помощью рассуждений занимает меньше времени, но в рассуждениях легко допустить ошибку.

Задача 2. Выяснить, кто из трёх людей участвовал в преступлении, исходя из двух посылок:

1) «Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал»;

2) «Если Иванов не участвовал, то Сидоров не участвовал».

Решение.

А – Иванов участвовал в преступлении;

В – Петров участвовал в преступлении;

С – Сидоров участвовал в преступлении.

Iспособ. С использованием таблицы истинности.

Конструируем формулы, соответствующие 1) и 2) посылке задачи: (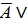В)→С и 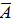→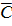. Так как обе посылки истинны, то составим таблицу истинности для конъюнкции полученных формул:

Таблица 2

Таблица истинности

Из таблицы видно, что преступление совершил А, то есть Иванов.

I аспособ. С помощью законов алгебры логики.

Снова запишем конъюнкцию формул, выражающих условия задачи. Преобразуем получившуюся формулу, пользуясь законами алгебры логики.

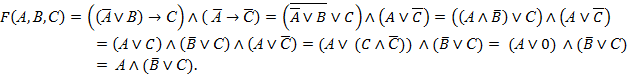
Так как обе посылки верны, то это выражение должно быть истинно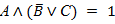. Это возможно только при А = 1, значит преступник – Иванов. Также 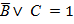, следовательно, исключается вариант B = 1, а C = 0, все остальные варианты возможны.

Ответ: исходя из предложенных посылок, можно определить, что Иванов участвовал в преступлении.

IIспособ. Cпомощью рассуждений.

Предположим, что Иванов не участвовал в преступлении, тогда выполняется условия 1 и 2. По условию 2 получается, что Сидоров не участвовал. Получается противоречие. Следовательно, Иванов участвовал, а про остальных нельзя сказать ничего определенного.

Решение данной задачи с помощью таблицы после ее построения сразу дает наглядный ответ. Решая задачу с помощью алгебры логики, наглядный ответ сразу получить сложно, для этого нужно делать определенные выводы. Минусы данного способа в том, что можно легко допустить ошибку, преобразуя формулы. Второй способ занимает меньше времени, но при рассуждениях легко запутаться в высказываниях.

Задача 3. Три одноклассника – Влад, Тимур и Юра встретились спустя 10 лет окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, а страсть третьего – регби.

Юра сказал, что на туризм ему не хватает времени, хотя его сестра – единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.

У двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.

Определите, кто чем любит заниматься в свободное время, и у кого какая профессия? [5, с. 385]

Решение.

Iспособ. Традиционная таблица. Кроме предложенного выше метода совмещения таблиц можно рассмотреть модификацию различных методов. Задача является трехмерной (множество имен, профессий и хобби), поэтому для ее решения используют кубическую таблицу [1, стр. 99].

Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист.

Так как у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен, то следует что буква «а», присутствующая в слове «врач», указывает на то, что врач не Влад, следовательно, врач – Тимур. Второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени является Юра.

В имени Тимур встречаются буквы «т» и «р», которые присутствуют в слове «туризм». Юра не юрист и не регбист, так как в его имени содержаться буквы «ю» и «р».

Из получившихся предположений можно составить следующую кубическую таблицу:

Таблица 3

Таблица соответствия имен, профессии и хобби

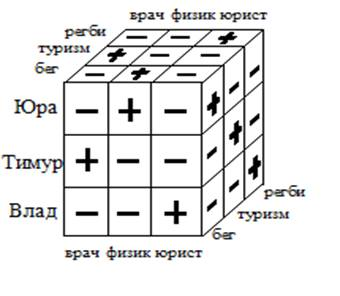
IIспособ. Нестандартная таблица.

Из высказывания Юры следует, что он не врач и не турист.

А из дальнейшего текста врач является туристом. Это отражает таблица.

Таблица 4

Таблица соответствия условий задачи

Далее из условия с буквами следует, что врач не Влад, следовательно, врач – Тимур; Юра не юрист и не регбист, так как в его имени содержаться буквы «ю» и «р». Можно составить следующую таблицу.

Таблица 5

Таблица соответствий условий задачи

Ответ:Влад – юрист и регбист, Тимур – врач и турист, Юра – физик и бегун.

Решая задачи с помощью традиционной и нестандартной таблиц, сразу после построения можно получить наглядный ответ. Нестандартная таблица удобная в применении, в ней наименьшая вероятность допустить ошибки. Минусы традиционной кубической таблицы в том, что для решения необходимо наличие опыта в заполнении такого рода таблиц.

Из приведенного выше анализа решения логических задач можно дать следующие рекомендации по применению того или иного способа:

1.                  Табличный метод и его модификации (кубическая и совмещенные таблицы, таблица соответствий) дают наглядность, логичность, прозрачность всех шагов рассуждений, следовательно, могут быть рекомендованы для решения задач любого уровня сложности.

2.                  Метод рассуждений можно рекомендовать только для решения простых задач с малым количеством объектов и множеств, так как при усложненном условии легко допустить ошибки, следовательно, он не дает уверенности в правильности решения.

3.                  Применение законов алгебры логики требуется осуществление перевода на язык математической логики, то есть выделяют элементарные высказывания и составляют более сложные в соответствие с условиями задачи. Следовательно, для применения этого способа необходимы знания законов Булевой алгебры и наличие опыта преобразований выражений и составлении таблицы. В то же время данный способ дает строгость и обоснованность полученных результатов.

Литература:

1. Бизам Д, Герцег Я. Многоцветная логика. – М.: Мир,1978. – 436 с.

2. Беррандо М. Занимательные задачи. – М.: Мир, 1983. – 457 с

3. Горбачев Н. Сборник олимпиадных задач по математике. – М: МЦНМО, 2004. – 560 с.

4. Игошин В.И. Математическая логика и теория алгоритмов. – 2-е изд. – М.: Изд. центр «Академия», 2008. – 448 с.

5. Сангалова М.Е. Курс лекций по математической логике. – Арзамас: Арзамас. гос. пед. ин-т, 2006. – 98 с.