Данная статья посвящена обзору различных способов решения геометрических задач с помощью метода «золотого сечения». Рассмотрен математический термин «золотое сечение», его основные свойства.
Ключевые слова: геометрическая задача, пропорции, иррациональное число, геометрическое построение, наглядность, интерактивные геометрические среды.
Abstract. This article reviews the different ways of solving geometric problems using the method of the Golden section. Considered a mathematical term «Golden section», its basic properties.
Keywords: geometric problem, proportions, irrational number, geometric construction, visualization, interactive geometric environment.
«Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора, а другое – деление отрезка в среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень».
Иоганн Кеплер
В повседневной жизни мы часто сталкиваемся с математическим термином «золотое сечение» сами того не подозревая. В живой природе«золотое сечение» встречается в некоторых видах морских звезд,раковинах моллюсков, рогах млекопитающих; в химиисечение встречается в белковых цепях нуклеиновых кислот; в медицине этот термин связывают с работой сердца и его мышечной системой; в архитектуре сечение представлено в различных проектах домов, в здании Кремля;в математике и геометрии «золотое сечение» образует геометрическую фигуру – икосаэдр, грани которого представлены 20 равносторонними треугольниками;также данный метод применятся для решения геометрических задач [3, с. 59]. Рассмотрим его более подробно.
В математике пропорцией (лат. proportio) называют равенство двух отношений:
a : b = c : d.
Отрезок прямой ВС можно разделить тремя способами:
· на две равные части, тогда отношение пропорции примет следующий вид: ВС:ВD=ВС:CD;
· на две неравные части в любом отношении, такие части не образуютпропорции;
· таким образом, когда ВС:BD=BD:CD.
Последнее разделение отрезка на части называется золотым делением или деление отрезка в крайнем и среднем отношении[1, с. 349].
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; и меньший отрезок так относится к большему, как больший ко всему[4, с. 50].
a : b = b : c или с : b = b : а.
Рассмотрим геометрическое смысл золотого сечения и выведем его приближенное значение.С математической точки зрения золотое сечение выразится через формулы квадратичной иррациональности.
 a
a
 |
ba-b
Рис. 1. Геометрическое изображение «золотого сечения»
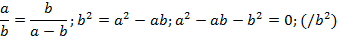
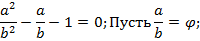
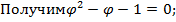
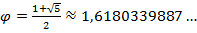 – показывает отношение большей части к меньшей.
– показывает отношение большей части к меньшей.
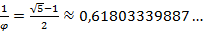 – показывает отношение меньшей части к большей.
– показывает отношение меньшей части к большей.
Итак, «золотое сечение» - это иррациональное число, приблизительно равное 1,618. Число 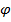 –является золотым сечением[1, с. 345].
–является золотым сечением[1, с. 345].
Впервые данный термин встречается в «Началах» Евклида (ок. 300 лет до н. э.).
Понятие «золотое сечение» или «золотое деление» в научный обиход ввел Пифагор, древнегреческий философ и математик.Рассмотрим некоторые виды задач, в решении которых используется принцип золотого сечения:
 Задача№1. Возьмите отрезок длиной 10 см и разделите его приблизительно в золотом отношении.
Задача№1. Возьмите отрезок длиной 10 см и разделите его приблизительно в золотом отношении.
 Получим два отрезка длиной 6,2 см и 3,8 см. Одна часть больше другой в 1,6 раза.
Получим два отрезка длиной 6,2 см и 3,8 см. Одна часть больше другой в 1,6 раза.
6,2 см 3,8 см
 |
10 см
Рис. 2. Разбиение отрезка в золотом отношении
Части золотого деления составляют приблизительно 62% и 38% всего отрезка.
Задача №2. Построить золотой прямоугольник.
Рассмотрим алгоритм построения золотого прямоугольника:
1. Начертим квадрат и разделим его на два равных прямоугольника.
2. В одном из прямоугольников проведем диагональ ВС.
3. Циркулем проведем окружность радиуса ВС с центром в точке В.
4. Продолжим основание квадрата до пересечения с дугой в точке L и проведем сторону KL параллельную стороне данного прямоугольника.












 ССN С К
ССN С К
1. 2. 3.4.
В ВВ М L
Рис. 3. Алгоритм построения золотого прямоугольника
ВС-радиус окружности; В-центр окружности
Измерьте линейкой длины сторон построенного прямоугольника MСKL и вычислите отношения большей стороны к меньшей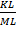 .Отношение сторон
.Отношение сторон 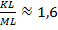 .
.
Так как число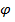 – иррациональное, то с помощью простых измеренийсделать это невозможно. Еще в древности мастера использовали циркуль и линейку, причем они рассмотрели различные способы построения. Разберем один из способов деления отрезка в золотом сечении.
– иррациональное, то с помощью простых измеренийсделать это невозможно. Еще в древности мастера использовали циркуль и линейку, причем они рассмотрели различные способы построения. Разберем один из способов деления отрезка в золотом сечении.
Решение:
Пусть дан отрезок ВС, применим к нему метод «золотое сечение».
Опустим перпендикуляр СА к отрезку ВС. Предположим, что длина отрезка ВС = 1.
Пусть длина отрезкаСА = 2ВС. СА=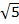 .
.
Из точкиА проведем окружность радиусом АК, где АК=ВС.
Тогда длина отрезка 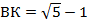 .
.
Затем проведем окружность с центром в точкеВ радиусом ВЕ. Длина отрезка 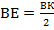 .
.
A

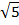
К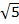
 Е
Е
B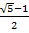 NC
NC
Рис.4. Золотое сечение отрезка ВС в точке N
Окружность с радиусом ВЕ пересечет отрезок ВС в точке N золотого сечения, так как 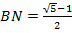 .
.
Задача№3.Вырежите из бумаги прямоугольник со сторонами 10 см и 16 см. Отрежьте от него квадрат наибольшей площади. Измерьте стороны получившегося прямоугольника.
Решение:
А К В



Д М С
Рис. 5. Построение золотого прямоугольника
Рассмотрим прямоугольник АВСД: Пусть стороны АВ=16 см, ВС=10 см. Тогда отношение сторон примет следующий вид: АВ:ВС=16:10=1,6.
Рассмотрим прямоугольник КВСМ: так как ВС=КМ=10 см, а КВ=АВ-АК=16-10=6 см. Получим следующееотношение сторон КМ:КВ=10:6=1,6666…см.
Рассмотрим прямоугольник МPNC: так как СN=ВС-ВN=10-6=4 см, а МС=ДС-ДМ=16-10=6 см, то отношение сторон МС:СN примет следующий вид МС:СN=6:4=1,5 см. Получили золотой прямоугольник
Задача№4. Построить золотое сечение отрезка ВС.

 Решение:Построить золотое сечение отрезка ВС, значит найти точкуК такую, что
Решение:Построить золотое сечение отрезка ВС, значит найти точкуК такую, что 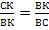 . D
. D



Е

 N
N
В К С
Рис. 6. Золотое сечение отрезка ВС
Рассмотрим прямоугольный треугольник DBC, у которого один катет в 2 раза больше другого. Проведем из точкиС перпендикуляр к прямой ВС и на нем отложим отрезок СD, длина которого равна половине стороны ВС.
СD=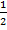 BC.
BC.
Затем, соединим точкиВ и D. Отложим отрезкиDE и ВКтак, что длина отрезка DE равна длине отрезка DC, а отрезокBK=АN.
Точка K является искомой, она производит золотое деление отрезка BC.
Нами было рассмотрено решение геометрических задач с помощью метода «золотого сечения». Использование предложенных видов заданий позволяет развивать творческие способности, исследовательские навыки и активизировать познавательную деятельность школьников, существенным образом интенсифицировать процесс обучения математике[2, с. 52].
Литература:
1. Золотое сечение. Три взгляда на природу гармонии / Шевелев И.Ш., Марутаев М.А., Шмелев И.П. – М.: Стройиздат, 1990. – С. 343-350.
2. Напалков С.В., Первушкина Е.А. WEB-КВЕСТ как средство развития инновационной стратегии образования // Приволжский научный вестник. – 2014. – № 8-2 (36).– С. 51-53.
3. Первушкина Е.А. Модель развития геометрической креативности школьников при обучении математике в 5-6 классах с использованием информационных технологий // Школа будущего. – 2011. – № 6. – с. 58-64.
4. Шевелев И.Ш. Геометрическая гармония // Наука и жизнь. – 1965. – № 8.– С. 14-26.







