Во многих практических ситуациях, связанных с работой в сложных загроможденных средах, находят применение манипуляторы с кинематической избыточностью. В этом случае не существует однозначного преобразования из пространства задания в пространство обобщенных координат. Ниже рассматривается задача управления движением одного класса избыточных манипуляционных систем, представляющих собой быстрый, малый, не избыточный манипулятор, установленный на медленной позиционирующей руке больших размеров (рис. 1).
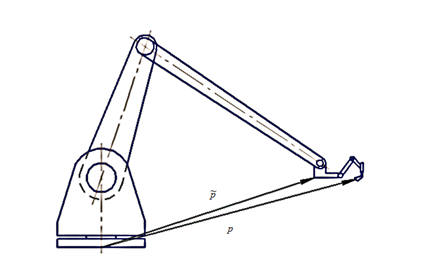
Рис. 1. Манипулятор
Задача управления избыточной манипуляционной системой по заданной в пространстве траектории разделена на два этапа: кинематический, связанный с формированием желаемых траекторий в степенях подвижности манипулятора с исключением вырождения системы и «потери» степеней свободы, и этап отслеживания заданной траектории. Конфигурация манипуляционной системы, приведенной выше, определена векторами 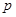 и
и 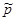 в неподвижной системе координат.
в неподвижной системе координат.
Вводится в рассмотрение расширенный вектор положения системы в координатном виде 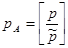 , dim(
, dim(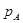 )=
)=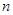 , где n — число степеней подвижности избыточной манипуляционной системы.
, где n — число степеней подвижности избыточной манипуляционной системы.
Когда задано желаемое положение рабочего органа 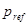 , можно из кинематических соображений выбрать
, можно из кинематических соображений выбрать 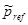 таким образом, чтобы не избыточный малый манипулятор находился в положении, близким к центру его рабочего пространства. Если позиционирующая часть избыточной манипуляционной системы имеет три степени подвижности и используется для того, чтобы обеспечить основанию малого манипулятора три поступательные степени свободы, вектор
таким образом, чтобы не избыточный малый манипулятор находился в положении, близким к центру его рабочего пространства. Если позиционирующая часть избыточной манипуляционной системы имеет три степени подвижности и используется для того, чтобы обеспечить основанию малого манипулятора три поступательные степени свободы, вектор 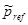 можно выбрать в соответствии с выражением
можно выбрать в соответствии с выражением 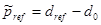 , (1)
, (1)
где 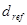 — поступательная составляющая вектора
— поступательная составляющая вектора 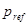 ;
; 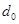 – постоянный вектор, определяющий положение центра рабочей зоны малого манипулятора по отношению к его основанию. Если позиционирующая рука имеет одну или две степень подвижности, то
– постоянный вектор, определяющий положение центра рабочей зоны малого манипулятора по отношению к его основанию. Если позиционирующая рука имеет одну или две степень подвижности, то 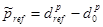 , (2)
, (2)
где 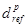 и
и 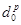 — проекции
— проекции 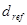 и
и 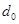 на степени свободы основания манипулятора [1].
на степени свободы основания манипулятора [1].
Расширенный вектор положения 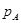 является функцией угловых координат робота
является функцией угловых координат робота 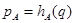 . (3)
. (3)
Если задан вектор 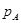 , то угловые координаты робота могут быть определены из обратного преобразования
, то угловые координаты робота могут быть определены из обратного преобразования 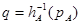 . (4)
. (4)
Таким образом, по заданному изменению 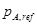 можно сформировать эталонную траекторию
можно сформировать эталонную траекторию 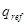 , которая должна быть отработана следящей системой [2].
, которая должна быть отработана следящей системой [2].
Уравнение движения n–звенного манипулятора может быть представлено в форме 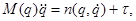 (5)
(5)
где 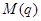 - матрица инерции;
- матрица инерции; 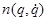 — вектор включающий себя кориолисовы центробежные члены, а также силы трения и тяжести;
— вектор включающий себя кориолисовы центробежные члены, а также силы трения и тяжести; 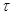 — вектор входных моментов. Взаимосвязь скорости и изменение положения в пространстве задания и скорости движения в угловой системе координат представляется соотношением
— вектор входных моментов. Взаимосвязь скорости и изменение положения в пространстве задания и скорости движения в угловой системе координат представляется соотношением 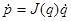 , (6)
, (6)
где 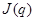 — матрица Якоби,
— матрица Якоби, 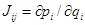 .
.
С использованием рассчитанной по динамической модели линеаризующей развязывающей обратной связи системы (5) можно привести к n несвязанным двойным интеграторам. В угловых координатах манипулятора его состояние определяется вектором 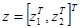 , где
, где 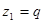 и
и 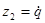 .
.
Используя закон правления вида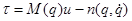 (7) можно привести результирующую модель замкнутой системы к форме
(7) можно привести результирующую модель замкнутой системы к форме 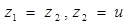 (8), где u — вектор управления системой, представляющий собой n несвязанных между собой двойных интегралов. Состояние системы в пространстве задания определяется вектором
(8), где u — вектор управления системой, представляющий собой n несвязанных между собой двойных интегралов. Состояние системы в пространстве задания определяется вектором 
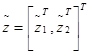 , где
, где 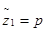 и
и 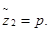
Закон управления вида 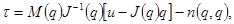 (9)
(9)
для системы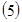 с учетом
с учетом 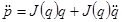 . (10)
. (10)
Описанный метод управления может быть использован для управления рассматриваемыми манипуляционными системами. Предполагается, что 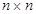 матрица Якоби расширенной системы
матрица Якоби расширенной системы 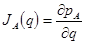 (12)
(12)
является неособенной. По аналогии с 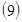 закон управления
закон управления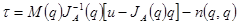 (13)
(13)
приводит к модели системы в пространстве состояний вида 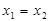 (14a)
(14a)
и 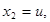 (14b)
(14b)
где 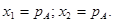 Синтез управления
Синтез управления 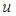 осуществляется из условия оптимизации показателя качества
осуществляется из условия оптимизации показателя качества 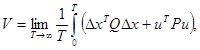 (15)
(15) 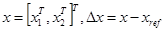 ,
, 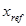 — заданное состояние системы;
— заданное состояние системы; 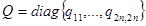 и
и 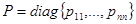 .
.
Поскольку требуемая точность отслеживания желаемого положения рабочего органа существенно выше точности отслеживания положения позиционирующей руки, весовые коэффициенты, соответствующие отклонениям положения рабочего органа выбираются более высокими, чем соответствующие отклонениям положения позиционирующей руки. Оптимальное управление имеет вид 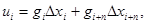 (16)
(16)
где 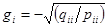 и
и 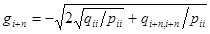 .
.
В закон управления могут быть дополнительно включены программная составляющая, рассчитанная по ускорению желаемого движения, и интегральный регулятор 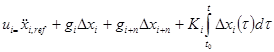 . (17)
. (17)
Вышеприведенный метод позволяет определить точное положение манипулятора в пространстве, а так же отследить его траекторию. Таким образом, манипулятор может быть использован при сборке кузовов автомобилей либо применяться в модулях ремонта кузовов.
Литература:
1. Поезжаева Е. В. Промышленные роботы: учеб.пособие: в 3 ч. — Пермь: Изд-во Перм. гос. тех. ун-та,2009. — Ч. 2. — 185 с.
2. Поезжаева Е. В., Васенин А. С., Шумков А. Г. Роботизация фермерских хозяйств по обработке растений / Е. В. Поезжаева, А. С. Васенин, А. Г. Шумков // Научно-технический журнал «Вестник» ВСГУТУ. — 2014 — Вып. 3 — С. 59–62.







