Выбор архитектуры локальной сети при проектировании систем реального времени

В данной работе сформулирована задача выбора архитектуры локальной сети при проектировании системы реального времени. Предложен метод решения задачи, основанный на построении графа передач данных, передаваемых между станциями сети, построении матрицы конфликтов, а также построения диаграммы, отображающей передачи данных в сети. Изложение метода сопровождается пояснениями на примерах.

 

Введение

В работе будем рассматривать систему реального времени организованную на многопроцессорной вычислительной системе. Данную систему отнесем к «жестким» системам реального времени, которые требовательны к времени выполнения и выработки управляющих воздействий на исполнительные механизмы. В связи с этим понятно стремление при проектировании сократить время реакции системы на управляющее воздействие. Основные потери времени приходятся на работу процессоров и на передачу данных в сети. Причем время на передачу данных в сети может оказаться соизмеримым или даже большим чем время затраченное процессором на обработку данных.

Сравнивать подходы проектирования компьютерных сетей в отличии от сетей реального времени, нельзя, т. к. для компьютерных сетей мы не знаем, что, когда и в каком объеме будет передаваться по сети. Задачей данной работы является построение сети с наибольшим распараллеливанием передач данных, чтобы сократить время на передачу данных.

Постановка задачи

Приступая к построению локальной сети, предварительно уясним содержание имеющихся исходных данных и целей задач, которые нам предстоит решить. Сведения, которыми мы располагаем для решения задач построения локальной сети, включают следующее:

-          число станций [1], объединить в сеть;

-          информационный граф программной нагрузки, в котором определены объемы данных, передаваемых между модулями позициями за один цикл моделирования [2];

-          распределение модулей и позиций по станциям, т. е. в информационном графе выделены дуги, требующие сетевой ресурс [3];

-          библиотека базовых сетей, в соответствии с которыми локальная сеть строится на основе одной или нескольких связанных между собой магистралей.

Информационный граф 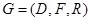 является двудольным взвешенным графом, где D — множество вершин данных  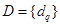с указанием для каждого  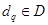размера требуемой памяти 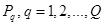; F — множество вершин модулей  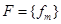с указанием для каждого  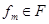величины потребляемого процессорного времени 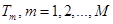;  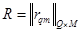— матрица объемов данных, передаваемых между вершинами графа G.

На графе G заданно разрезание [3] на множество подграфов 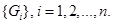 Число подграфов n соответствует числу станций вычислительной системы. Вершины подграфа G_i по требуемой памяти P_q и процессорному времени T_m суммарно не превышают ресурсы станции s_i по памяти P(s_i) и процессорному времени T(s_i). Величина T(s_i) равна числу временных тактов, которые процессор станции s_i может выделить для выполнения модулей подграфа G_i за один цикл моделирования.

Разрезанию {G_i} соответствует множество С ребер графа G, 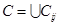, где с_ij — множество ребер, связывающих между собой подграфы G_i и G_j. Каждому ребру c_qm, связывающему вершину d_q и f_m в графе G, соответствует элемент r_qm матрицы R. Поэтому объем данных, передаваемых в сети между станциями s_i и s_j можно определить величиной r_ij,

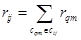.                                                                                                                  (1)

Таким образом, общий объем передаваемых по сети данных за один цикл моделирования для разрезания {G_i} составит величину r,

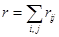.                                                                                                                       (2)

Если пропускную способность магистрали сети обозначить величиной 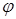, определяющей объем данных, передаваемых за один такт моделирования, то для успешной работы локальной сети, построенной на базе одной магистрали, должно выполняться условие:

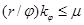.                                                                                                                 (3)

Здесь 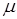 — число временных тактов в одном цикле моделирования; k_φ — коэффициент, учитывающий факторы снижения значения φ в реальной сети.

Очевидно, что решить проблему своевременной передачи данных в сети путем увеличения числа μ нельзя, так как величина r также зависит от μ. Поэтому, если условие (3) не выполняется, то это означает, что сеть на одной магистрали с параметром 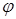 не работоспособна и необходимо принятие решений по уменьшению величины r или увеличению значения параметра φ. Среди таких решений могут быть следующие:

-       найти другое разрезание с более низким значением r;

-       увеличение пропускной способности магистрали;

-       изменить архитектуру сети.

Наиболее предпочтительным является решение с поиском допустимого разрезания с лучшей оценкой r. Для нашего примера будем считать, что поиск наилучшего разрезания завершен. Второе решение отражает вполне естественное стремление использовать магистраль с более высокой пропускной способностью, например с 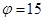. Очевидно также, что выбор и использование магистрали с более высоким значением  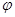не всегда возможны. Третий вид решений связан с построением сети на основе нескольких магистралей. Основные условия здесь направлены на поиск вариантов распараллеливание передач данных в сети.

Предположим, что первые два вида решений исчерпаны, также как и многие другие, связанные, например, с изменением информационного графа, условий поступления входных и обновления выходных данных и другими изменениями в программной нагрузке. Рассмотрим решения по выбору архитектуры сети, построенной на базе нескольких магистралей с неизменной пропускной способностью φ, способной за цикл моделирования передать объем данных r. Перед изложением метода решения данной задачи приведем ряд примеров объединения нескольких магистралей в сеть и условий их загрузки при передаче данных.

Анализ базовых вариантов сетей

В первую очередь нужно определить число магистралей в сети. Ориентировочно это можно сделать исходя из отношения 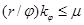. Полученный результат округляется в большую сторону и принимается как минимально возможное число магистралей в сети способных выполнить программную нагрузку. Приведем примеры сетей с различным числом магистралей. Варианты архитектур сетей будем считать базовыми и создадим для их хранения библиотеку. Базовые сети отражают различные конфигурации связи нескольких магистралей. На рис. 1 приведены примеры четырех базовых сетей с двумя, тремя и четырьмя магистралями.

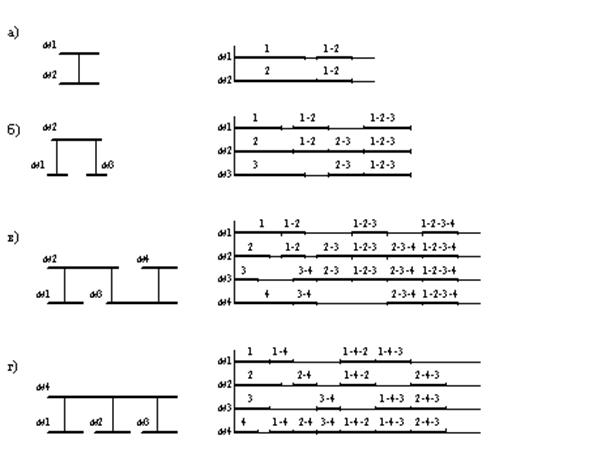
Рис. 1. Примеры базовых сетей и диаграмм загрузки магистралей

 

А также для каждой из архитектур построим диаграмму, которая показывает возможную загрузку магистралей сети при передаче данных между станциями. При этом предполагается, что к каждой магистрали подключается не менее двух станций, а передачи данных осуществляются как между станциями одной магистрали, так и между станциями разных магистралей. Длины отрезков, отражающих суммарные объемы передач данных в сети, выполняемые в разные моменты времени за один цикл моделирования, принимаются произвольными и измеряются числом тактов моделирования затрачиваемых для передачи соответствующих объемов данных. Над каждым отрезком указан перечень магистралей, принимающих участие в передаче данных. Например, запись 1–4-2 над отрезками диаграммы (рис. 1, г) обозначает загрузку магистралей М1, М4, М2 при передаче данных между станциями, подключенными к магистралям М1 и М2. Здесь имеется в виду, что например для варианта сети на рис. 1, г в отрезок 1–4-2 будут собраны все передачи, выполняемые между станциями С₃ и С₇, С₄ и С₆, С₄ и С₇, С₅ и С₇ в разные моменты времени в интервале одного цикла моделирования. Заметим также, что параллельно с этой передачей могут передаваться данные между станциями, подключенными к магистрали М3, то есть отрезок 3 на диаграмме рис. 1, г, может размещаться параллельно отрезкам 1–4-2.

Анализ приведенных на рис. 1 базовых сетей по соответствующим диаграммам позволяет сделать ряд выводов. В сети (а) станции желательно подключать к магистралям М1 и М2 так, чтобы отрезки 1 и 2 были примерно равны, а отрезок 1–2 был минимальной длины. Для сети (б) критичной по загрузке является магистраль М2. В сети (в) такими магистралями являются М2 и М3, а в сети (г) магистраль М4. Для данных сетей наилучшим вариантом подключения станций к магистралям будет такой вариант, который обеспечивает равную и минимальную загрузку магистралей. Например, для сети (б) условие равенства загрузки магистралей можно записать в виде: [1]+ [1–2]= [2]+ [1–2]+ [2–3]= [3]+ [2–3]. Здесь квадратные скобки обозначают длину соответствующих отрезков. Аналогичные условия равенства загрузки магистралей можно записать для сетей (в) и (г). Минимально возможная загрузка магистралей достигается в случае, если подключение станций к магистралям удается выполнить таким образом, что между станциями, подключенными к разным магистралям, данные не передаются.

Метод решения задачи построения сети

При изложении метода решения задачи выбора базовой сети и варианта подключения станций к магистралям будем придерживаться примера информационного графа, представленного на рис. 2. Количеству станций равному 6. Кружками здесь показаны данные d_q, а планками — модули f_m. У каждого ребра, связывающего вершины d_q и f_m проставлены веса r_qm, равные объему данных, передаваемых между вершинами d_q и f_m за один цикл моделирования [2]. Пунктирными линиями выделены подграфы разрезания и указаны номера станций, ресурсы которых занимают данные подграфы.

Пусть пропускная способность магистралей составляет 10 единиц объемов передаваемых данных за 1 такт, то есть величина 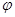=10, коэффициент k_φ=1,3, а цикл моделирования μ равен 12 тактам. Тогда для принятого варианта распределения модулей и данных по станциям можно определить ориентировочное число магистралей сети. Для этого на основе матрицы R согласно (2) вычисляем общий объем данных r, передаваемых между станциями. Для нашего примера r=198 единиц. Время на передачу данных составит  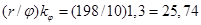тактов, что превышает цикл моделирования более чем в 2 раза. Таким образом, определяем, что в сети должно быть не менее трех магистралей. В данном случае при условии, что к магистрали подключается не менее 2-х станций, фактически выбирать более 3 магистралей не имеет смысла.

Исходя из имеющихся сведений о числе станций, распределения по ним модулей информационного графа, общей загрузке сети и рекомендации по числу магистралей задачу, выбора структуры сети можно сформулировать следующим образом. Необходимо выбрать структуру базовой сети и варианта подключения станций к магистралям сети так, чтобы по возможности большая часть данных могла передаваться между станциями сети параллельно.

 

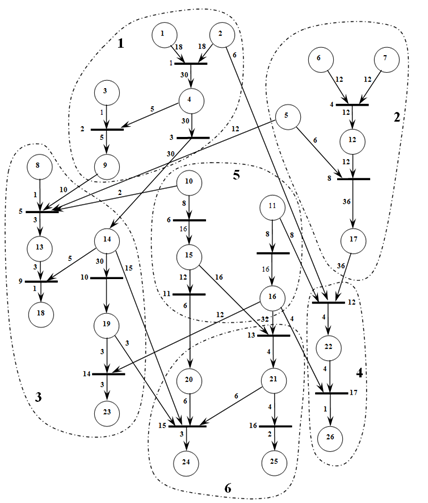
Рис. 2. Пример информационного графа

 

Метод решения задачи основан на выявлении в сети возможностей параллельных передач данных для различных вариантов подключения станций к магистралям базовой сети. С этой целью выполняется совокупность операций по построению следующих объектов:

-        строится граф передачи данных между станциями сети;

-        выполняется разрезание графа передач данных на минимально связанные подграфы;

-        выбирается вариант подключения станций к магистралям сети;

-        строится матрица наличия конфликтов между передачами данных при доступе к магистралям сети;

-        строится диаграмма совмещения параллельных передач данных.

Граф передачи данных P=(S,Z,R) строится на основе варианта распределения модулей и данных графа G по станциям и матрицы весов 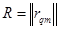. Вершина  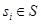графа P соответствует станции s_i, на которую распределены модули и данные подграфа G_i разрезания {G_i}. Наличие ребра  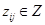соответствует тому, что подграфы G_i и G_j связаны между собой ребрами графа передач данных 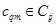, то есть 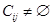. Каждому ребру  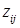графа P ставится в соответствие величина r_ij, которая вычисляется по выражению (1) и определяет объем данных, передаваемых между станциям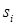и  и 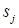 за один цикл моделирования.

Пример графа P, построенного для разрезания, показанного на рис. 2, представлен на рис. 3. Граф P содержит 6 вершин –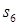, по числу станций. Вариант разрезания графа на три его подграфа на рис. 3 выделен пунктирными линиями. К каждой магистрали следует подключать не менее двух станций. Поэтому в данном примере на каждую магистраль приходится подграф, содержащий 2 станции.

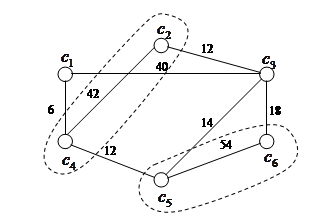
Рис. 3. Граф передачи данных P

 

Веса r_ij ребер z_ij, представленные на рис. 3, получены по выражению (4) и в сумме составляют 198 единиц.

Построение матрицы наличия конфликтов Q осуществляется на основе графа P и варианта подключения станций к магистралям выбранной базовой сети. Методику построения матрицы Q покажем на рассматриваемом примере. В качестве базовой структуры сети выберем вариант с тремя магистралями, представленный на рис. 1, б. На рис. 4, а, показан один из вариантов подключения станций к магистралям данной сети.

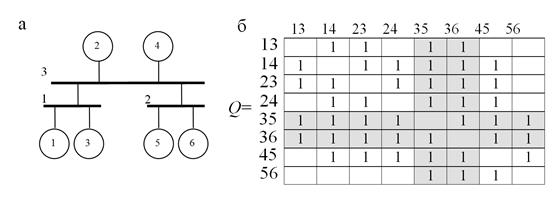
Рис. 4. Вариант архитектуры сети и матрица наличия конфликтов: а) вариант подключения станций к базовой сети; б) матрица наличия конфликтов Q

 

Размерность матрицы Q определяется числом ребер графа P. Множество ребер 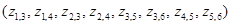 графа P обозначим соответствующими кодовыми номерами, сохранив в них номера станций. Получим множество кодовых номеров ребер (13, 14, 23, 24, 35, 36, 45, 56) и, соответственно, номеров строк и столбцов матрицы Q. Так, например, номер ребра 24, означает наличие передач данных между станциями 2 и 4 с объемом  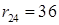единиц. Элемент  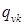матрицы наличия конфликтов  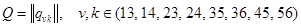определяется следующим образом:  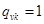если пары станций ребер v и k при передачи данных в сети (рис. 4, а) имеют конфликт по доступу к магистрали и  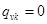в противном случае.

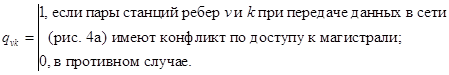
Так, например, элемент 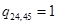, так как при одновременной передаче данных между станциям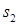и  и 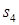 и станциям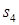и  и 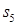 имеет место конфликт за доступ к магистрали. Напротив, элемент 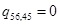, так как и при одновременной передаче данных в парах станци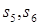й  и 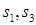 конфликта за доступ к магистрали не будет. Это объясняется тем, что в данном случае используются разные магистрали. Построенная таким образом матрица Q представлена на рис. 4, б.

В матрице Q на рис. 4, б, строки и столбцы 35, 36 выделены. Они отличаются тем, что у них все элементы 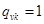, 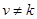. Это означает, что при передаче данных между соответствующими станциями, например, для строки 35 — это станции s₃ и s₅, заняты все три магистрали и параллельно с парой s₃, s₅ не могут выполняться передачи данных между станциями во всех других парах. Поэтому выделенные строки и столбцы могут быть исключены из матрицы Q.

На основе матрицы Q строится диаграмма совмещения параллельных передач данных. Для удобства построения диаграммы матрица Q принимается в качестве матрицы связности вершин графа. Соответствующий граф Q представлен на рис. 5, а. Вершины 35, 36 в граф Q не вошли по изложенной выше причине. Включать эти вершины в граф Q нет смысла, так как при передаче данных в соответствующих парах станций происходит захват всех магистралей сети и, следовательно, передачи данных в других парах станций параллельно с назваными невозможны. В скобках у вершин графа Q указанны объемы данных, передаваемых между соответствующими станциями.

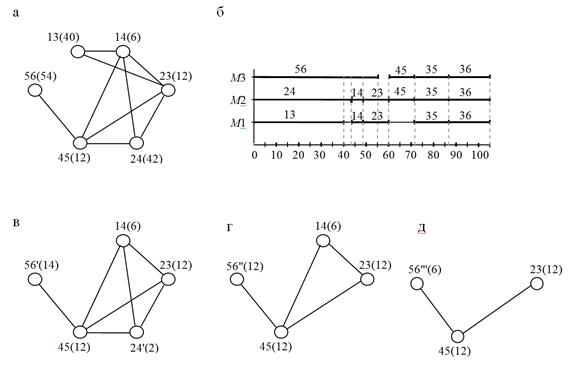
Рис. 5. Построение диаграммы передач данных: а — граф Q; б — диаграмма совмещения передач данных; в, г, д — преобразования графа Q при построении диаграммы

 

Для построения диаграммы в графе Q последовательно выделяются максимальные пустые подграфы [3] и объемы передач соответствующих вершин совмещаются на диаграмме (рис. 5, б). Так, на первой стадии выделяется максимальный пустой подграф, например, с вершинами 13, 56, 24 и соответствующие объемы 40, 54 и 42 единицы могут передаваться в сети параллельно и, следовательно, на диаграмме они совмещаются. Вершины с минимальным объемом передач данных исключаются из графа Q. В данном случае это вершина 13, а вершины 56' и 24' сохраняются в графе с новыми объемами 14 и 2 единицы (рис. 5, в) и помечаются штрихами. При формировании следующего максимального пустого подграфа вершины, помеченные штрихами, выбираются в первую очередь. Для графа на рис. 5, в, выбираются вершины 56' и 24'. Вершина 24' исключается, и процесс продолжается для графа на рис. 5, г. Здесь выбираются вершины 56" и 14. Вершина 14 исключается, а для графа на рис. 5, д, максимальный пустой подграф включает вершины 56" и 23. Обе они последовательно исключаются из графа и оставшаяся вершина 45 отражается на диаграмме.

Заметим, что при построении диаграммы (рис. 5, б) объемы передаваемых данных для каждой вершины графа отражаются на всех магистралях, участвующих в передаче этих данных. Построение диаграммы завершается отражением объемов передач для вершин 35 и 36, помеченных в матрице Q и не вошедших в граф Q.

Из диаграммы следует, что суммарный объем передач данных в сети с учетом их совмещения составляет 104 единицы или 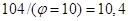 временных тактов, что укладывается в цикл моделирования 12 тактов. Однако при этом коэффициент k_φ достигает лишь величины 1,15. Общий объем передач данных согласно графа P составляет 198 единиц. Таким образом, для выбранной локальной сети и варианта подключения станций, представленного на рис. 4, а, последовательная цепь передач данных за счет использования параллельных передач сокращается с 198 до 104 единиц. Соответственно сокращается время передач с 19,8 до 10,4 тактов. Оценивая сокращение времени передач, следует иметь в виду, что выигрыш в 9,4 такта несколько сокращается на величину задержек в адаптерах, связывающих магистрали в сети.

Заключение

В результате исследований, выполненных в данной работе, удалось формализовать переход от плана использования ресурсов, получаемого при решении задачи распределения модулей и данных информационного графа по станциям вычислительной системы, к задаче выбора архитектуры ее локальной сети с минимальными затратами времени на передачу данных при выполнении программной нагрузки.

Результат, полученный при решении задачи выбора архитектуры сети, в общем случае следует рассматривать как один из возможных. Действительно, если в полученной сети изменить подключение станций к магистралям, то изменится матрица конфликтов и, соответственно, диаграмма. Последовательная цепь передач данных может измениться в большую или меньшую сторону. Поэтому для поиска наилучшего варианта структуры сети, доставляющего наибольшее совмещение параллельных передач данных, нужно перебрать множество приемлемых базовых сетей и для каждой из них сформировать и оценить множество вариантов подключения станций. При формировании вариантов подключения станций решения принимаются на основе анализа графа передач данных и структуры базовой сети.

Эксперименты показали, что для сетей на основе 2–4 магистралей с подключением до 10 станций перебор базовых сетей и поиск наилучших вариантов подключения станций с использованием изложенных правил не приводит к большим объемам вычислений. При дальнейшем увеличении размерности сетей необходимо наряду с предложенными выше разработать дополнительные более эффективные правила отсеивания неперспективных вариантов сетей на основе сопоставления весов ребер графа передач данных и структуры графа конфликтов базовой сети.

 

Литература:

 

1.                Погребной А. В. Определение числа и топологии размещения станций многопроцессорной вычислительной системы // Известия Томского политехнического университета. — 2006. — Т. 309. — № 7. — С. 160–164.

2.                Погребной А. В. Определение объемов передач данных в сети вычислительной системы для заданной модели программной нагрузки // Известия Томского политехнического университета. — 2007. — Т. 310. — № 3. — С. 103–107.

3.                Кристофидес Н. Теория графов. Алгоритмический подход. — М.: Мир, 1978. — 432 с.