При анализе и синтезе технических объектов используются их математические модели. При этом математические модели либо известны, либо получены вручную.
Известные математические модели указывают на отработанную методику получения модели электромеханических устройств. Методики являются универсальными для электромеханических устройств различных конструкций. Описания получения этих математических моделей практически нигде нет. Процессы в синхронном двигателе на данный момент плохо изучены и мало где освещены. Для получения математической модели нужно получить исходные математические выражения из процессов в синхронном двигателе. Для вывода каких-либо формул сделаем сначала математическое описание синхронного двигателя с постоянными магнитами, далее построем электрическую и геометрическую схему замещения СДПМ, из которых получим уравнения электрического равновесия, потокосцепления и получим в итоге уравнения электромагнитного момента в общем виде.
Применение постоянных магнитов в магнитных системах синхронных машин так же, как и в других типах электрических машин, обусловлено стремлением уменьшить габариты и вес машины, упростить конструкцию, увеличить КПД, повысить надежность в эксплуатации.
Постоянные магниты в синхронных машинах предназначены для создания магнитного поля возбуждения, причем для этого могут применяться постоянные магниты, комбинированные с электромагнитами по катушкам которых протекает постоянный ток. Синхронные машины, являются машинами переменного тока. Применяются в качестве двигателя и генератора.
Многие синхронные машины с постоянными магнитами имеют две статорные обмотки. Это обусловлено тем, что минимальное количество обмоток на статоре, которое обеспечивает создание вращающегося электромагнитного поля, равно двум. Такую конструкцию имеют двухфазные синхронный тахогенератор (СТГ) и синхронный двигатель c постоянными магнитами (СДПМ).
У СДПМ на две статорные обмотки, сдвинутые в пространстве на 90°, подаются напряжения переменного тока (сдвинутые по фазе относительно друг друга также на 90°). Протекающие по обмоткам токи создают магнитное поле, которое вращается в пространстве с частотой питающих напряжений. Это поле увлекает за собой постоянный магнит ротора, заставляя последний вращаться. У математической модели СДПМ входными переменными являются питающие напряжения на обмотках, а выходными — угловая скорость ротора. При получении математической модели СДПМ принимается ряд упрощающих допущений:
1) магнитная проводимость магнитопровода бесконечно большая по сравнению с магнитной проводимостью воздуха, из-за чего конфигурация магнитного поля полностью определяется конфигурацией воздушного зазора и все электромагнитные процессы протекают в воздушном зазоре между статором и ротором;
2) отсутствуют вихревые токи (поэтому отсутствуют соответствующие им контуры схемы замещения), гистерезис (поэтому собственные индуктивности обмоток не зависят от знака протекающих через них токов) и насыщение (поэтому индуктивности статорных обмоток не зависят от величины протекающих через них токов).
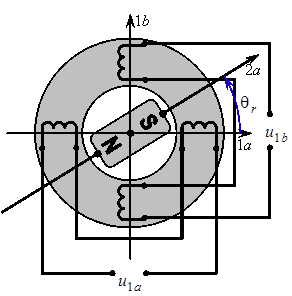
Рис. 1.1. Конструкция двухфазного СДПМ
СДПМ могут быть двухполюсными (Рисунок 1.1), но в общем случае имеют несколько пар полюсов pн. Некоторые параметры СДПМ (индуктивности и потокосцепления обмоток) могут зависеть от геометрического угла поворота ротора θr. В этом случае число пар полюсов сказывается на этих параметрах, а также на токах и электромагнитном моменте.
Для СДПМ существует электрическая схема замещения и геометрическая.
Электрическая схема замещения является упрощённым изображением обмоток и постоянных магнитов для определения уравнений электрического равновесия.
Электрическая схема замещения содержит столько контуров, сколько имеется фазных обмоток (Рисунок 1.2). Каждый контур содержит резистор, представляющий активное сопротивление обмотки 1a и 1b, напряжение питания обмотки 1a и 1b, и ЭДС, которая отражает индуктивные свойства обмотки 1a и 1b.
Между обмотками 1a и 1b существует связь через взаимную индуктивность обмоток 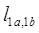 . Магнитный поток постоянного магнита ротора взаимодействует с обмотками 1a и 1b,создавая в них потокосцепления
. Магнитный поток постоянного магнита ротора взаимодействует с обмотками 1a и 1b,создавая в них потокосцепления 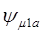 и
и 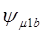 . В результате взаимодействия питающих напряжений и ЭДС, в обмотках протекают токи
. В результате взаимодействия питающих напряжений и ЭДС, в обмотках протекают токи
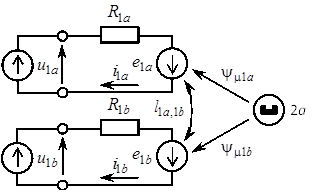
Рис. 1.2. Электрическая схема замещения двухфазного СДПМ
Статор СДПМ, как правило, неявнополюсный, а ротор может быть как неявнополюсным, так и явнополюсным. Неявнополюсные СДПМ имеют сравнительно равномерный неферромагнитный зазор между статором и ротором и при вращении ротора условия для прохождения через этот зазор магнитного потока практически не меняются. Явнополюсные СДПМ имеют неравномерный зазор между статором и ротором и при вращении ротора магнитная проводимость для магнитного потока существенно зависит от угла поворота ротора, что необходимо учитывать при получении математического описания.
В большинстве случаев СДПМ явнополюсные, но вариант с неявнополюсным СДПМ имеет большое методологическое значение, так как позволяет более наглядно представить общие принципы получения математического описания, а его сравнение с явнополюсным вариантом выявляет степень влияния явнополюсности на математическую модель и режимы работы.
При получении математических моделей СДПМ возможны дополнительные идеализирующие допущения о геометрической и электрической симметрии, а также о форме питающих напряжений.
Геометрическая схема замещения является упрощённым изображением обмоток для определения углов, в зависимости от конструкции двигателя (Рисунок 1.3).
Для построения геометрической схемы замещения задаются оси обмоток статора 1a и 1b и угол между осями обмоток статора 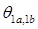 . На осях размещаются соответствующие фазные обмотки и запитываются соответствующими напряжениями
. На осях размещаются соответствующие фазные обмотки и запитываются соответствующими напряжениями 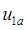 и
и 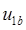 .
.
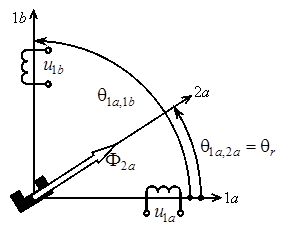
Рис. 1.3. Геометрическая схема замещения двухфазного СДПМ
Размещается ротор в виде условного обозначения постоянного магнита и с ним связывается ось 2a. Постоянный магнит создаёт магнитный поток, представляемый вектором
и с ним связывается ось 2a. Постоянный магнит создаёт магнитный поток, представляемый вектором 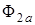 . Ось ротора располагается относительно оси 1a под углом
. Ось ротора располагается относительно оси 1a под углом 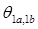 и вращается вместе с ротором. Угол между осью ротора и осью 1a и является углом поворота ротора
и вращается вместе с ротором. Угол между осью ротора и осью 1a и является углом поворота ротора 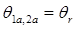 .
.
Двухфазный СДПМ содержит две обмотки на статоре, запитанные напряжениями 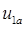 ,
, 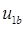 , и постоянный магнит на роторе, создающий магнитный поток
, и постоянный магнит на роторе, создающий магнитный поток 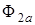 . На роторе всегда располагается только один магнит, не зависимо от числа фаз. Индекс 2a у магнитного потока в данном случае означает, что ось ротора совпадает с магнитной осью «север — юг» этого магнита.
. На роторе всегда располагается только один магнит, не зависимо от числа фаз. Индекс 2a у магнитного потока в данном случае означает, что ось ротора совпадает с магнитной осью «север — юг» этого магнита.
Уравнения электрического равновесия:
На основании электрической схемы замещения записываются уравнения электрического равновесия (по второму закону Кирхгофа): для обмотки 1a и для обмотки 1b:
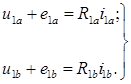 (1)
(1)
В соответствии с законом электромагнитной индукции (Фарадея) ЭДС выражаются через производные потокосцеплений по времени:
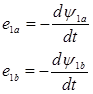 (2)
(2)
Выражения для ЭДС подставляются вместо ЭДС, производные выносятся в левую часть. Получилась система обыкновенных дифференциальных уравнений в нормальной форме (в форме Коши):
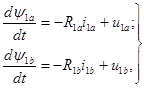 (3)
(3)
где индексами 1a и 1b помечены величины, относящиеся к соответствующим обмоткам; u — напряжения питания; e — наводимые в обмотках ЭДС; R — активные сопротивления обмоток; i — токи в обмотках; ψ — потокосцепления обмоток.
Параметрами формулы (3) являются сопротивления обмоток 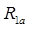 ,
, 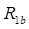 , внешними воздействиями являются напряжения питания
, внешними воздействиями являются напряжения питания 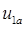 ,
, 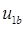 , переменными состояния являются токи
, переменными состояния являются токи 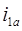 ,
, 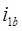 и потокосцепления
и потокосцепления 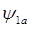 ,
, 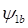 .
.
Выражения потокосцеплений обмоток на основании пространственной схемы замещения СДПМ:
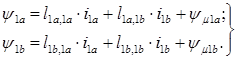 (4)
(4)
где 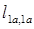 ,
, 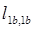 — собственные индуктивности, соответственно, фаз 1a и 1b;
— собственные индуктивности, соответственно, фаз 1a и 1b; 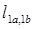 =
=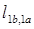 — взаимные индуктивности между фазами (которые всегда равны между собой);
— взаимные индуктивности между фазами (которые всегда равны между собой);
ψμ1a, ψμ1b — потокосцепления постоянного магнита с соответствующими фазами статора.
В общем виде все электромагнитные параметры СДПМ могут зависеть от угла поворота ротора.
Электромагнитный момент в общем виде:
Для получения математической модели электродвигателя необходимо получить выражение электромагнитного момента. Момент представляет собой произведение силы на плечо. В электродвигателе сила представляет собой результат взаимодействия магнитного поля статора с магнитным полем ротора. Поля могут создаваться электрическим током или формироваться с помощью постоянных магнитов.
Выражение электромагнитного момента можно получить с использованием закона сохранения энергии. В этом случае учитывается только количество обмоток и их расположение в пространстве в общем виде.
С учётом закона сохранения энергии её преобразование в электрической машине выглядит следующим образом (Рисунок 1.4):
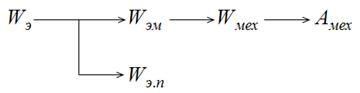
Рис. 1.4. Преобразование энергии в электрической машине
где 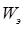 — исходная электрическая энергия от источника питания;
— исходная электрическая энергия от источника питания;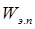 — энергия электрических потерь;
— энергия электрических потерь;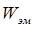 — энергия электромагнитного поля;
— энергия электромагнитного поля;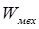 — механическая энергия;
— механическая энергия;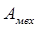 — механическая работа, она же реализованная механическая энергия.
— механическая работа, она же реализованная механическая энергия.
Работа при вращательном движении есть произведение момента сил на угол поворота и равна работе механической:
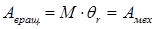 (5)
(5)
Механическая работа равна механической энергии и равна электромагнитной энергии (Рисунок 1.4):
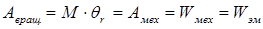 (6)
(6)
Работа на малом участке угла поворота соответствует расходованию малой порции электромагнитной энергии, получаем уравнение элементарной энергии:
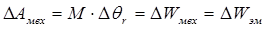 (7)
(7)
Отсюда можно получить выражение для электромагнитного момента:
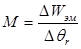 (8)
(8)
При переходе к бесконечно малому приращению угла поворота получают производную по углу поворота:
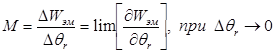 (9)
(9)
Получена производная по углу поворота, а не по времени, поэтому она показана как частная производна.
Для получения выражения электромагнитного момента следует получить выражение электромагнитной энергии. В электродвигателе электромагнитная энергия создаётся постоянными магнитами и обмотками при протекании по ним электрического тока. Из физики известно выражение электромагнитной энергии:
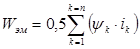 (10)
(10)
где n — число обмоток.
Потокосцепление формируется от собственного тока, токов других обмоток и от постоянных магнитов (если они есть). Оно представляет собой суммарный магнитный поток от всех источников, пронизывающий обмотку, умноженный на число её витков.
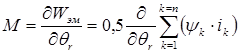 (11)
(11)
Тогда электромагнитный момент определяется как частная производная этого выражения электромагнитной энергии по углу поворота.
Полное потокосцепление представляется через индуктивности и токи, а также через потокосцепления от постоянных магнитов ротора.
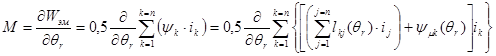 (12)
(12)
Знак дифференцирования вносим под знак суммирования индуктивностей, и потокосцеплений от постоянных магнитов ротора.
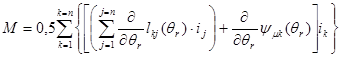 (13)
(13)
Токи не зависят от угла поворота, но только от времени. Поэтому они не дифференцируются, а выполняют роль постоянных коэффициентов.
Получено математическое описание процессов в синхронном двигателе, построена электрическая и геометрическая схема замещения СДПМ, получены уравнения электрического равновесия, потокосцепления, уравнения электромагнитного момента в общем виде. Полученное математическое описание можно использовать в различных вычислениях (анализа и синтеза).
Литература:
1. Бронов С. А. Регулируемые электроприводы переменного тока: Монография / Бронов С. А., Овсянников В. И., Соустин Б. П. — Красноярск: КГТУ, 1998. 273 с.
2. Бронов С. А., Марарескул А. В. Автоматизированное проектирование электромеханических систем: учеб. пособие для самостоятельного изучения. URL: http://www.files.lib.sfu-kras.ru/ebibl/umkd/180/u_sam.pdf (дата обращения: 29.11.2014).







