Приведён обзор и сравнительный анализ методов выделения корней, соответствующих угловому положению пеленгуемых источников радиоизлучения (ИРИ), среди множества паразитных корней, которые являются результатом пеленга ИРИ с помощью алгоритма редукции ранга.
Ключевые слова: UCA‑Root‑Rare, полином, АРР
На страницах настоящего журнала уже был освещён алгоритм редукции ранга (АРР) [1–3], в зарубежной литературе обозначаемый аббревиатурой UCA‑Root‑Rare. Однако одним из серьезных недостатков АРР является наличие ложных корней, не соответствующих угловому положению пеленгуемых ИРИ. Известно несколько методов отбраковки ложных корней, кратко рассмотренные в настоящей статье.
Метод Böhme-Pesavento
Этот метод был предложен авторами алгоритма и описан в [4]. Метод предполагает 5-ти этапную процедуру или нахождение корней дополнительного компенсирующего полинома:
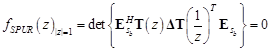 (1)
(1)
Другими словами, корни, соответствующие угловым положениям ИРИ 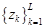 могут быть получены из корней следующего полиномиального выражения:
могут быть получены из корней следующего полиномиального выражения:
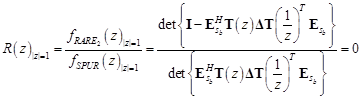 (2)
(2)
Как утверждают авторы, ложные корни в числителе 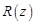 нейтрализуются ложными корнями знаменателя, так что на единичной окружности остаются только те решения, которые соответствуют угловым положениям ИРИ.
нейтрализуются ложными корнями знаменателя, так что на единичной окружности остаются только те решения, которые соответствуют угловым положениям ИРИ.
Однако в случае конечной выборки сигнальные и ложные корни обоих полиномов смещаются от их идеальных позиций на единичной окружности, что приводит к не идентичности ложных корней. В этом случае используют следующую 5-ти этапную процедуру:
- Шаг 1. Вычислить подпространство сигнала 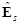 и подпространство шума
и подпространство шума 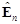 ковариационной матрицы
ковариационной матрицы 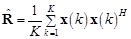 .
.
- Шаг 2. Найти потенциальные сигнальные корни 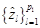 среди наибольших корней
среди наибольших корней 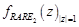 внутри единичной окружности, где
внутри единичной окружности, где 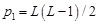 .
.
- Шаг 3. Найти потенциальные ложные корни 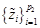 среди наибольших корней
среди наибольших корней 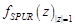 внутри единичной окружности, где
внутри единичной окружности, где 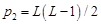 .
.
- Шаг 4. Выполнить цикл:
○ Для 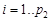
○ Определить сигнальные корни 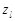 , полученные в шаге 2, минимизируя
, полученные в шаге 2, минимизируя 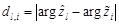 , где
, где 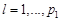 .
.
Если 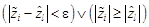 то
то
удалить 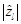 из множества потенциальных сигнальных корней;
из множества потенциальных сигнальных корней;
удалить 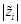 из множества потенциальных ложных корней.
из множества потенциальных ложных корней.
Закончить.
Закончить.
- Шаг 5. Оценить сигнальные корни 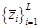 найденные из наибольших
найденные из наибольших 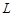 корней, оставшихся среди потенциальных сигнальных корней.
корней, оставшихся среди потенциальных сигнальных корней.
К сожалению, последующие исследования, проведённые в работах [5, 6], показали, что при определённых угловых положениях предложенный метод неверно выделяет координаты, соответствующие заданным угловым положениям. Несостоятельность данного метода проявляется в следующих случаях:
1) когда азимутальный угол одного из источников равен среднеарифметическому значению азимутальных углов двух других ИРИ, то есть 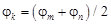 . При этом попытка устранения зеркальной координаты для одного из источников
. При этом попытка устранения зеркальной координаты для одного из источников 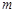 или
или 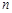 может привести к удалению истинной координаты
может привести к удалению истинной координаты 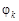 рисунок 1.
рисунок 1.
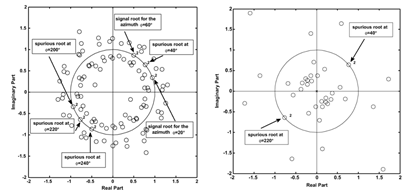
Рис. 1. Эффект скрытия пеленга, продемонстрированный в [5]
2) когда координата одного источника отличается от координаты другого источника на 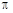 , например
, например 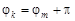 . В этом случае количество корней на единичной окружности не всегда эквивалентно числу источников. Следовательно для того чтобы получить окончательные значения пеленга необходимо знать априорную информацию о структуре источников;
. В этом случае количество корней на единичной окружности не всегда эквивалентно числу источников. Следовательно для того чтобы получить окончательные значения пеленга необходимо знать априорную информацию о структуре источников;
3) в статье не упоминается о симметричности корней полинома относительно начала координат. К тому же симметричные корни не учитывались при последующем угломестном оценивании, что в конечном результате приводит к ошибкам пеленга.
В связи с обнаруженными недостатками, авторами [] был предложен собственный метод.
Метод нуль пространства
Предлагаемый авторами [5] основан на компенсации эффекта взаимного влияния антенных элементов и дополнительно предполагает поиск нуль пространство специальной матрицы, что позволяет сразу найти угол места ИРИ и избавиться от ложных корней. Рассмотрим, предлагаемую авторами процедуру:
- Шаг 1. Вычислить циркулянтный вектор взаимного влияния 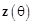 для различных углов места методом приёмного взаимного импеданса, описанного в [7], и построить таблицу для
для различных углов места методом приёмного взаимного импеданса, описанного в [7], и построить таблицу для 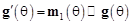 ,
, 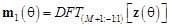 ,
,  ,
, 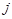 — мнимая 1,
— мнимая 1, 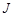 –функция бесселя первого рода,
–функция бесселя первого рода, 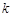 –номер возбуждаемой фазовой моды.
–номер возбуждаемой фазовой моды.
- Шаг 2. Получить пеленг по азимуту, используя АРР для пространственной функции:
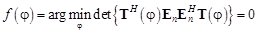 (3)
(3)
Приведённая выше пространственная функция используется вместо (2) для устранения эффекта скрытия пеленга. На этом шаге всё ещё существуют ложные корни, но они буду исключены в конце парного двухмерного вычисления пеленга с использованием параметрического поиска на следующем шаге.
- Шаг 3. Для каждого корня (азимута), включая ложные решения, вычислить матрицу 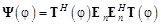 и построить матрицу
и построить матрицу 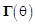 её нуль-пространства.
её нуль-пространства.
- Шаг 4. Используя одномерный параметрический поиск в диапазоне 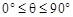 , найти все углы места, соответствующие
, найти все углы места, соответствующие 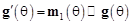 и принадлежащие нуль пространству матрицы
и принадлежащие нуль пространству матрицы 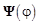 . Если
. Если 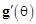 не принадлежит нуль пространству матрицы
не принадлежит нуль пространству матрицы 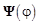 , то такой корень считается ложным и должен быть удалён из списка потенциальных корней. Парное двухмерное значение пеленга, найденное в ходе одномерного параметрического поиска, будет окончательным. На данном этапе дополнительно происходит компенсация эффекта взаимного влияния
, то такой корень считается ложным и должен быть удалён из списка потенциальных корней. Парное двухмерное значение пеленга, найденное в ходе одномерного параметрического поиска, будет окончательным. На данном этапе дополнительно происходит компенсация эффекта взаимного влияния 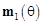 .
.
Метод Гуссинса и Роджера
Альтернативный метод вычисления угловых координат при пеленге ИРИ был предложен в работе [6].
С помощью АРР, определяются азимутальные углы 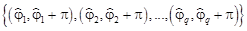 , причем для их нахождения не требуется информация о зенитных углах. Оценки, сделанные с помощью АРР, дают q пар азимутальных углов. При этом если на решетку приходит L сигналов, то вообще говоря q ¹ L, поскольку сигналы могут характеризоваться одинаковым зенитным углом.
, причем для их нахождения не требуется информация о зенитных углах. Оценки, сделанные с помощью АРР, дают q пар азимутальных углов. При этом если на решетку приходит L сигналов, то вообще говоря q ¹ L, поскольку сигналы могут характеризоваться одинаковым зенитным углом.
Покажем теперь, каким образом, зная пары азимутальных углов, определяются зенитные углы. Расширим область определения вектора отклика однородной кольцевой антенной решётки (ОКАР) радиуса 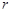 из
из 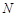 элементов в области зенитных углов следующим образом
элементов в области зенитных углов следующим образом
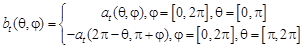 (4)
(4)
Функцию 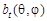 , которая обладает периодом 2p по обеим угловым переменным, можно представить в виде разложения в двумерный ряд Фурье
, которая обладает периодом 2p по обеим угловым переменным, можно представить в виде разложения в двумерный ряд Фурье
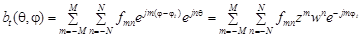 (5)
(5)
где 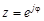 ,
, 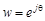 .
.
Данное разложение приближается к точному значению, если выполняются условия
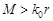 (6)
(6)
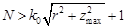 (7)
(7)
В пространстве лучей вектор отклика может быть записан как
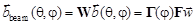 (8)
(8)
где
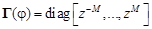 (9)
(9)
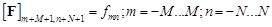 (10)
(10)
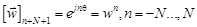 (11)
(11)
Алгоритм MUSIC в пространстве лучей принимает вид
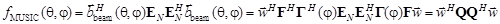 (12)
(12)
где 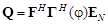 . Для заданной пары азимутальных углов
. Для заданной пары азимутальных углов 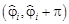 определяют матрицу Q и ищут нули по углу q. Фазы комплексных нулей, которые оказываются максимально близкими к единичной окружности, служат для оценки зенитных углов
определяют матрицу Q и ищут нули по углу q. Фазы комплексных нулей, которые оказываются максимально близкими к единичной окружности, служат для оценки зенитных углов 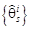 при s = 1...Si. В зависимости от значения углов
при s = 1...Si. В зависимости от значения углов 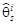 их приписывают к одной из пар углов по азимуту
их приписывают к одной из пар углов по азимуту 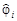 или
или 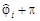
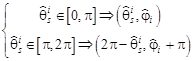 (13)
(13)
При выполнении данной процедуры могут появиться паразитные нули, которые не соответствуют реальным направлениям прихода ИРИ. Для решения проблемы выбираются лишь L самых малых значений. Можно также записать:
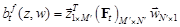 (14)
(14)
где 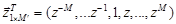 ,
, 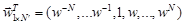 ,
, 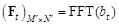 ,
, 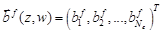 .
.
Введем вспомогательную матрицу
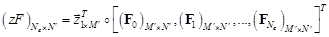 (15)
(15)
где индекс 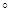 означает поэлементное умножение, и сформируем матрицу
означает поэлементное умножение, и сформируем матрицу
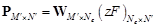 (16)
(16)
Тогда
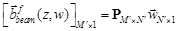 (17)
(17)
Теперь (12) перепишем как
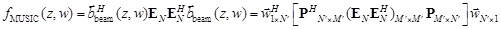 (18)
(18)
Из (18) следует, что матрица 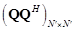 , оказывается равной матрице
, оказывается равной матрице 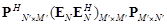 , и теперь при заданном значении азимутального угла можем использовать алгоритм ROOT–MUSIC для нахождения корней полинома по степеням
, и теперь при заданном значении азимутального угла можем использовать алгоритм ROOT–MUSIC для нахождения корней полинома по степеням 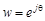 .
.
Выводы. Сравнительный анализ трех вышеупомянутых методов приводит к следующему. Метод Bohme-Pesavento, не смотря на свою простоту, предполагает либо точного знания ковариационной матрицы пеленгуемого сигнала, что на практике невозможно, поскольку выборка ограниченна, либо выполнения пятиэтапной процедуры получения азимута, из множества потенциальных корней, расположенных на расстоянии 0,01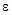 от единичной окружности. При этом авторами не учитываются не только корни расположенные симметрично относительно начала координат, но и корни симметрично расположенные относительно единично окружности. Такие типы корней не учитываются при дальнейшем вычислении угла места ИРИ. Сама процедура вычисления угла места у авторов [] предполагает поиск спектра полиномиальной АРР-матрицы, что является сложной в вычислительном и временном отношении затратной процедурой.
от единичной окружности. При этом авторами не учитываются не только корни расположенные симметрично относительно начала координат, но и корни симметрично расположенные относительно единично окружности. Такие типы корней не учитываются при дальнейшем вычислении угла места ИРИ. Сама процедура вычисления угла места у авторов [] предполагает поиск спектра полиномиальной АРР-матрицы, что является сложной в вычислительном и временном отношении затратной процедурой.
Метод поиска нуль пространства матрицы, предложенный в [5], несмотря на необходимость проведения процедуры одномерного поиска по углу места и выяснения принадлежности вектора к нуль пространству матрицы, имеет одно существенное преимущество перед методом Bohme-Pesavento. Он (метод) учитывает наличие паразитных связей между антенными элементами или взаимный имепданс антенных элементов, который, как показано в [7], имеет угломестную зависимость. Но процедура вычисления нуль пространства и одномерный поиск сказываются на быстродействии выполнении пеленга предлагаемым методом поиска нуль пространства.
Как альтернативу, предложенную в [3], авторы расширяют область определения в угломестной плоскости и выполнить двухмерное преобразование Фурье полученной диаграммы направленности ОКАР, а затем применить вычислительно эффективный алгоритм Root для поиска угла места по известным оценкам азимута. Однако такое искусственное расширение может привести к неоднозначности значений пеленга по углу места.
Литература:
1. Коробков М. А. Алгоритм UCA–Root–Rare для задач пеленгования источников радиоизлучения однородной кольцевой антенной решёткой // Молодой ученый. — 2014. — № 13. C47–54
2. Коробков М. А. Метод сокращения вычислительных затрат в алгоритме UCA‑Root‑Rare // Молодой ученый. — 2014. — № 14. C. 88–90.
3. Коробков М. А. Методы нахождения корней полинома в алгоритме пеленгования UCA-Root-Rare в пакете Mathcad // Молодой ученый. — 2014. — № 14. — С. 54–56.
4. Pesavento M., Böhme J. F. Direction of arrival estimation in uniform circular arrays composed of directional elements // Sensor Array and Multichannel Signal Processing Workshop. 2002. No 8. P. 503–507.
5. B. H. Wang, H. T. Hui, M. S. Leong. Decoupled 2D Direction of Arrival Estimation Using Compact Uniform Circular Arrays in the Presence of Elevation-Dependent Mutual Coupling. IEEE Transactions on antennas and propagation, Vol. 58, No. 3, march 2010, стр.747–755.
6. R. Goossens and H. Rogier. “A hybrid UCA-RARE/Root-MUSIC approach for 2‑Ddirection of arrival estimation in uniform circular arrays in the presence of mutual coupling,” IEEE Trans. Antennas Propag., vol. 43, pp. 841–849, 2007.
7. H. T. Hui, “Improved compensation for the mutual coupling effect in a dipole array for direction finding,” IEEE Trans. Antennas Propag., vol.51, no. 9, pp. 498–2503, Sep. 2003.







