Графтар теориясына негіз болған есептердің бірі Кенигсберг көпірлері туралы есебі болған. Бұл есепті алғаш рет Л.Эйлер графтар теориясы арқылы қарастырған болатын. Бұдан 100 жыл өткен соң әсіресе Англияда жаратылыстану ғылымының барынша әр түрлі формадағы саласында графтар теориясы пайдаланыла бастады. Электр тізбегі мен кристалл моделіндегі молекуланың структурасын зерттеуге, сондай-ақ ойындар теориясы мен программалауда, биология мен психологияда, сонымен қатар математикадағы логикалық есептерді шешуде кеңінен қолданылады.
Логикалық есептер деп арнайы формула қолданылмайтын және әрқайсысы өзінше талдау жасауды қажет ететін есептерді айтамыз. Математикалық логиканы жетік түсінбейінше, оны меңгеру өте қиын. Себебі қазіргі кезде ғылым мен техника қарыштап дамыған сайын ол адамның ойлау қабілетінің ең ірі жетістіктері болып табылады.
Графтар арқылы кейбір математикадағы логикалық есептерді шешуге болады, сондықтан әсіресе граф көптеген логикалық есептерді оңай жолдармен шығаруға, есептерді шешуде және олардың шығару жолдарын адам есіне лезде сақтап қалу үшін де көмектеседі. Логикалық есептер адамның ойлау қабілетінің дамуына әсер етеді және арттырады.
Граф ұғымында көптеген қолданбалы есептер, соның ішіндегі айналамызды қоршаған ортаның әртүрлі объектілері арасындағы байланыстар жүйесі зерттеледі. Объектілер төбелер деп аталып, нүктелер арқылы белгіленеді, ал төбелер арасындағы байланыстар доғалар деп аталып, сәйкес нүктелерді қосатын бағытталған түзулермен белгіленеді.
Графтар арқылы төменде қарастырылған есептерді шешу жолдарын қарастыралық.
№1 есеп. Симфониялық оркестр скрипкада, флейтада, альтте, кларнетте, гобойда және трубада ойнай алатын үш музыкантты: Браун, Смит және Вессонды жұмысқа қабылдады.Бізге белгілі болсын:
1. Смит ең ұзыны;
2. Скрипкада ойнай алатынының бойы флейтада ойнай алатынан кіші;
3. Скрипкада және флейтада ойнай алатындар мен Браун пиццаны ұнатады;
4. Альтист пен трубач арасында керіс болғанда, Смит оларды достастыруға тырысты;
5. Браун трубада да, гобойда да ойнай алмайды.
Әр музыкант екі инструментте ойнай алатын болса, олардың қайсылары неде ойнай алады?
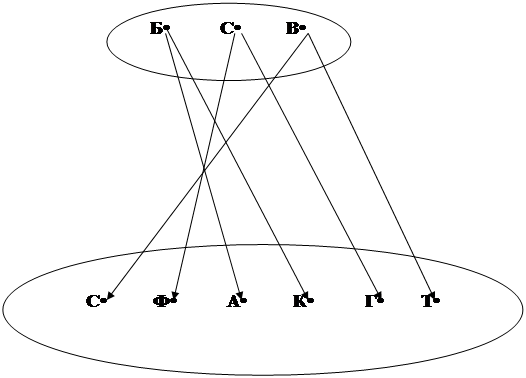
Есептің шешуі. Есептің шартына сәйкес екі жиынға тиісті етіп нүктелерді аламыз. Бірінші жиында үш музыкант Б,С,В нүктелерімен,ал екінші жиында инструменттер алтау болғандықтан С,Ф,А,К,Г,Т нүктелерімен белгіленеді.
Музыканттар үшеу, инструменттер алтау болғандықтан әрқайсысы екі инструментте ойнайды делік. 4 шарт бойынша Смит альтта да, трубада да ойнамайды, ал 3 пен 5 шатқа сәйкес Браун скрипкада, флейтада, трубада және гобойда ойнай алмайды. Сондықтан Браун альт пен кларнет инструменттерінде ойнайтын болғаны. Осы пікірлерді қанағаттандыратындай етіп есептің сызбасын граф арқылы көрсетелік:
Есептегі берілген шартқа сәйкес екі жиындағы нүктелерді бағытталған түзулермен қосамыз (1-сурет).
|
1-сурет.
Есепті қорыта келе, Браун альт және кларнетте, Смит —флейта мен гобойда, Вессон — скрипка мен трубада ойнайды деген шешімге келеміз.
№2 есеп. Әділ, Ербол, Қанат мектеп бітіргеннен соң он жылдан кейін кездескен. Келесі шарттарға сәйкес:
1.Олар дәрігер, физик, юрист мамандық иесі болған.
2.Туризмнің, жүгірудің, регбидің біреуін ғана ұнатады.
3.Ерболдың туризмге уақыты жоқ, бірақ жанұясындағы жалғыз дәрігер, қарындасы –турист. Дәрігер қызметтестерінің қызығатын істерімен бөліседі.
4.Таңқаларлығы, достардың екеуінің бос уақытында айналысатын жұмыстары мен мамандығының аттарындағы бір әрпі де өз атымен сәйкес келмейді.
Кімнің мамандығы қандай және бос уақытында немен айналысатынын неше әдіспен анықтауға болады?
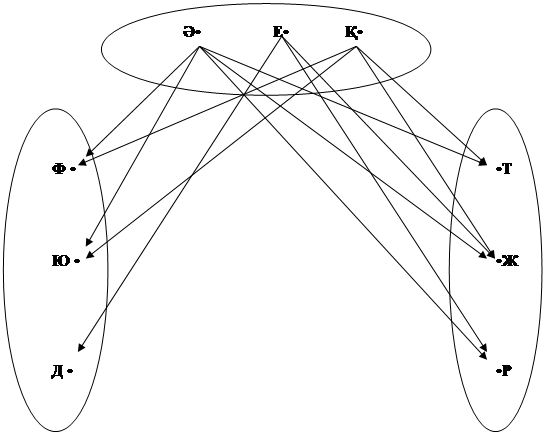
Есептің шешуі. Берілген мәліметтерді үш жиынға топтастыруға болады, яғни аты, мамандығы, қызығушылығы. Әр жиындағы нүктелерді сәйкес әріптермен белгілейміз. Ерболдың сөзінен туризмді қаламайтынын, дәрігер екендігін білдік. Қызығушылықтары- жүгіру мен регби. Әділдің мамандығы физик немесе юрист болса, ал қызығушылықтары-туризм, жүгіру, регби. Қанаттың мамандығы физик немесе юрист болса, ал қызығушылықтары-туризм, жүгіру, регби (2-сурет).
2-сурет. |
Есептің шешу жолын қорыта келе, мынадай шешімге келеміз. Бірінші әдіс бойынша, демек Әділдің мамандығы физик болса, онда қызығушылығы туризм болсын делік. Қанаттың мамандығы юрист, ал қызығушылығы жүгіру болады. Ерболдың мамандығы есептің шартында айтылғандай дәрігер, қызығушылығы регби.
Екінші әдіс бойынша Әділдің мамандығы юрис болса, онда қызығушылығы регби, ал Қанаттың мамандығы физик, ал қызығушылығы туризм болады. Ерболдың мамандығы есептің шартында айтылғандай дәрігер, ал қызығушылығы жүгіру.
Тақырыпты пысықтауға арналған тапсырмалар:
Тапсырма-1. Айгүл, Анар, Әсел және Жаңабек әртүрлі домбыра, гитара,сырнай және скрипка аспаптарында ойнайды. Бұл студенттер сонымен қатар әртүрлі ағылшын, француз, неміс және испан шет тілдерін меңгерген. Белгілі шарттар:
1.Олардың сырнайда ойнайтыны испанша сөйлей алады.
2. Анар скрипкада, домбырада ойнамайды, ағылшын тілін білмейді.
3. Айгүл скрипкада, домбырада ойнамайды, ағылшын тілін білмейді.
4. Ал немісше сөйлейтіні домбырада ойнамайды.
5.Әсел француз тілін біледі, бірақ скрипкада ойнамайды.
Кім қандай аспапта ойнайды және қандай тілді меңгерген?
Тапсырма-2. Жүгіруден жарысқа 4 дос қатысты: Асан, Бақыт, Боран және Азат. Достар алғашқы 4 орынды иеленді. Кім қандай орын алды? – деген сұраққа олар былай жауап берді:
1.Асан: мен екінші, ал Бақыт екінші.
2.Боран: мен екінші, ал Асан бірінші.
3.Азат: мен екінші, ал Бақыт төртінші.
Егер біреуінің жауабы ақиқат, қалғандарынікі жалған болса, кім қандай орын алғаны?
Тапсырма-3. Жауапқа тартылған Айбек, Батыр және Саят деген азаматтар былайша түсініктеме берді:
1. Айбек: Батыр кінәлі, ал Саят кінәлі емес.
2. Батыр: Айбек кінәлі емес немесе Саят кінәлі.
3. Саят: Мен кінәлі емеспін, ал Айбек пен Батырдың біреуі кінәлі.
Сонда кім кінәлі екенін анықтау керек?
Әдебиет:
1. Жаңбырбаев Б.С., Добрица В.П. Математикалық логиканың бастамалары: Оқу құралы – Алматы: Абай атындағы АлМУ, 2001.
2. Ершов Ю. Л., Палютин Е. А. Математическая логика. - СПб., Лань., 2004.
3. Игошин А. А. Математическая логика, теория алгоритмов, - М., Академия, 2004.
4. Хаггарти Р. Дискретная математика для программистов / Пер.с англ.. – М.: Техоссфера, 2003. - 320 с.