В статье рассматривается специфический вид информационной модели — учебная компьютерная модель. Перечислены наиболее важные части такой модели. Кратко описана технология осуществления визуализации объекта изучения с помощью OpenGL.
Ключевые слова:вычислительный эксперимент, компьютерная визуализация, компьютерное моделирование, нитяной маятник, бифилярный подвес, модель, учебная модель, учебные компьютерные модели, OpenGL.
Информационная модель — это, в той или иной форме, описание объекта моделирования [4; с. 7]. Особый вид таких моделей — это учебные информационные модели, то есть такие, которые предназначены для обучения. Так как в настоящее время, особенно в физике, широкое применение получило компьютерное моделирование, которое позволяет автоматизировать сам процесс моделирования, то можно говорить о внедрении в процесс обучения учебных компьютерных моделей. Вычислительный эксперимент (эксперимент с использованием компьютерных моделей объектов) может заменить в случае необходимости натурный эксперимент [6; 7]. Часто в таких моделях реализована компьютерная визуализация [2]. Она предполагает отражение свойств изучаемого объекта с помощью внешних чувственно воспринимаемых образов, формирование понятий в сознании обучающихся и формирование у них эмпирического мышления [8; 9]. Это отражение внешних, воспринимаемых обучающимся свойств, осуществляется, как правило, с помощью особого визуального представления — образной модели. Кроме того, считается, что понимание физического явления возникает тогда, когда человек может построить для этого явления адекватную математическую модель [3]. Учебная компьютерная модель (фактически — компьютерная программа) является частью человеко-машинной системы, с помощью которой осуществляется процесс обучения. В этом случае важным является то, каким образом осуществляется информационное взаимодействие внутри этой системы. В настоящее время оно чаще всего осуществляется посредством графического интерфейса данного компьютерного приложения. Таким образом, важными частями учебной компьютерной модели являются образная модель, математическая модель и пользовательский интерфейс (рис. 1) [5].

Рис. 1. Составные части учебной компьютерной модели
В этой статье мы рассмотрим только процесс создания образной модели, то есть той части учебной компьютерной модели, которая непосредственно отвечает за визуализацию объекта изучения. Кроме того, мы ограничимся только случаем, когда моделируется поведение объекта реального мира, который обучающийся может видеть в природе (исключаются визуализации, предполагающие изображение абстрактных объектов, реально в природе не существующих и являющихся модельным представлением в сознании человека). Наиболее оправданным с точки зрения наглядности в данной ситуации будет трехмерное образное представление объекта изучения, так как в случае необходимости его можно свести к двумерному представлению. Будем считать, что объект изучения может двигаться в пространстве. Иными словами, его движение и будет являться предметом учебного исследования. Демонстрация движения в этом случае осуществляется с помощью анимации — специального метода, предполагающего создание серии изображений объекта изучения в отдельных фазах его движения, с помощью которого во время показа их на экране у обучающегося возникает впечатление движения объекта.
Перечислим этапы подготовки к визуализации анимированной трехмерной сцены [10, с. 17]:
- геометрическое моделирование сцены, создание объектов и их пространственная привязка;
- топологическая привязка объектов, создание кинематической схемы, определение изменения характеристик объектов с течением времени для анимации;
- задание физических свойств объектов, наложение текстур, задание отражения, прозрачности и других свойств;
- определение физических свойств среды, настройка атмосферных и гравитационных эффектов;
- расстановка и настройка источников света, выбор точек наблюдения, установка камер;
- выбор модели освещения, визуализация (рендеринг).
Рассмотрим процесс подготовки и осуществления компьютерной визуализации на примере нитяного маятника, представляющего собой груз, подвешенный на бифилярном подвесе (рис. 2). Такой маятник при определенных условиях можно считать математическим.
Рис. 2. Математический маятник — тело на бифилярном подвесе
Как правило, мы создаем образные 3D-модели в обучающих программах с помощью библиотеки OpenGL, которая является частью операционной системы. Это означает, что приложение, использующее OpenGL, не нуждается в дополнительных программах, кроме стандартных, содержащихся на любом компьютере с установленной операционной системой Windows [11, с. 7]. Создаваемые нами приложения являются многооконными (рис. 3). Одно окно специально отводится для визуализации объекта изучения [1].
Визуальный образ моделируемого маятника состоит из шара и двух линий, обозначающих подвес. Подвес крепится к цилиндру небольшого диаметра. Так как решалась задача, в которой длина подвеса маятника могла изменяться, на экране присутствует еще один цилиндр, обозначающий планку, ограничивающую движение верней части подвеса (рис. 3). Кроме того, изображаются дополнительные линии, с помощью которых легче анализировать движение маятника: линия, обозначающая равновесное положение маятника, и перпендикулярная ей линия, соответствующая верхним точкам подвеса маятника. Таким образом, визуальный образ состоит из линий и графических примитивов двух типов: двух цилиндров и одного шара. Можно усложнить визуальную картину, если добавить в нее транспортир (диск) с нанесенными на него метками (линиями) (рис. 3). Также в программе можно предоставить пользователю возможность масштабирования изображения маятника и перенос точки наблюдения за его движением. Часто мы повышаем качество компьютерных образов и получаем некоторые специальные эффекты, используя наложение текстур на графические примитивы и добавление источников света, хотя это можно не считать обязательным требованием к виду образной модели.
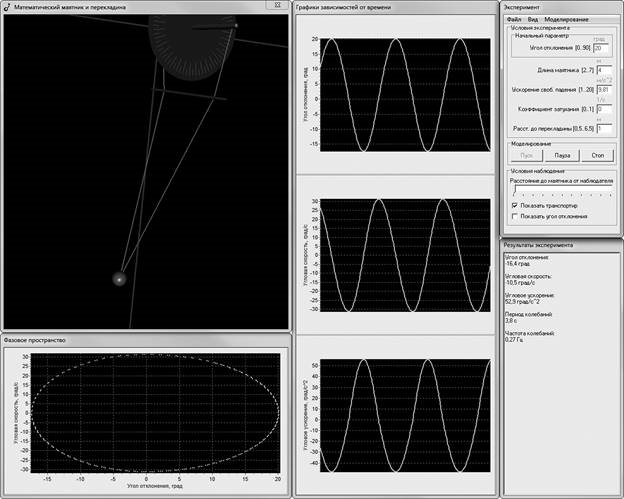
Рис. 3. Окна приложения, моделирующего движение математического маятника
В заключении отметим, что OpenGL, позволяет достаточно легко рисовать трехмерные объекты, при этом от создателя такой графики иногда даже не требуется знаний формул транспонирования матриц. Мы имеем большой опыт создания учебных компьютерных моделей с использованием технологии OpenGL. Технология используется уже достаточно давно, тем не менее программы, написанные еще во времена массового использования Windows XP, могут быть использованы до сих пор на современных операционных системах Windows 7 и 8.1.
Литература:
1. Данилов О. Е. Дизайн компьютерных приложений для визуализации информации об учебных компьютерных моделях / О. Е. Данилов // Молодой ученый. — 2014. — № 13. — С. 26–36.
2. Данилов О. Е. Изучение интерференции с помощью компьютерного моделирования / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 9. — С. 50–58.
3. Данилов О. Е. Использование компьютерной модели математического маятника при изучении механических колебаний в курсе физике / О. Е. Данилов // Молодой ученый. — 2014. — № 18. — С. 17–24.
4. Данилов О. Е. Компьютерное моделирование колебательного движения. Численные методы решения задач: учебно-методическое пособие / О. Е. Данилов, А. Ю. Трефилова. — Глазов: Глазов. гос. пед. ин-т, 2012. — 36 с.
5. Данилов О. Е. Обучение компьютерному моделированию на примере создания компьютерной модели кругового математического маятника / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 10. — С. 80–87.
6. Данилов О. Е. Применение имитационного моделирования механических взаимодействий при обучении физике / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2014. — № 5. — С. 97–103.
7. Данилов О. Е. Сочетание натурного и вычислительного экспериментов в обучении физике / О. Е. Данилов // Молодой ученый. — 2014. — № 19. — С. 10–11.
8. Данилов О. Е. Учебная компьютерная модель физического маятника / О. Е. Данилов // Молодой ученый. — 2014. — № 15. — С. 49–52.
9. Данилов О. Е. Формирование умения проводить теоретическое исследование при изучении распределения физической величины в пространстве с помощью компьютерной модели / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 7. — С. 84–94.
10. Крапивенко А. В. Технологии мультимедиа и восприятие ощущений: учебное пособие / А. В. Крапивенко. — М.: Бином. Лаборатория знаний, 2012. — 271 с.
11. Краснов М. В. OpenGL. Графика в проектах Delphi. — СПб.: БХВ-Петербург, 2004. — 352 с.







