Определяется роль и формирование когнитивной компетентности при математическом моделировании сложных систем различной природы. Приводятся примеры.
Ключевые слова:математическое моделирование, когнитивная компетентность, формирование.
Рост математической культуры специалистов привел к проникновению математических методов в различные сферы человеческой деятельности. Однако на практике оказывается, что одних лишь математических познаний еще недостаточно для решения конкретной прикладной задачи. Требуются навыки перевода исходной формулировки задачи на математический язык (в этом и состоит проблема овладения искусством математического моделирования): подходы к описанию и анализу реальной задачи, возможности ее математической идеализации, выбор путей построения модели, оценка пригодности и соответствия объекту, методы проверки модели. К сожалению, этот наиболее существенный творческий этап работы редко находит отражение не только в учебниках, тяготеющих к аксиоматическому, законченному изложению соответствующих дисциплин, но и в большинстве и других научных публикаций. Не претендуя на разработку систематического руководства по математическому моделированию, ниже на конкретных примерах показывается, как в настоящее время осуществляется математическая постановка и обработка реальных прикладных задач, относящихся к управлению движением, медицине, психологии и др. В основе, как правило, лежит когнитивное моделирование системы [1…3]. Поэтому основное внимание нами и уделяется формированию когнитивной компетентности на примерах математического моделирования сложных систем различной природы.
Моделирование эргатических систем. Рассмотрим класс эргатических (человеко-машинных) систем, где объект управления моделируется системой нелинейных обыкновенных дифференциальных уравнений (часто специального вида) с переменными коэффициентами [4]. Предполагается справедливость действия в этой системе организмического принципа [5], в соответствии с которым объект предопределяет поведение оператора. Анализ и синтез таких систем связаны с разработкой методик определения параметров, соответствующих эталонному нормальному функционированию системы (в том числе характеризующих деятельность человека-оператора), а также методов объективной оценки деятельности оператора по данным эталонного управления и соответствующих числовых характеристик конкретных реализаций управлений. В дальнейшем предполагается разработка программно-алгоритмических модулей.
Здесь при когнитивном моделировании используется формализованное понятие управляющего воздействия оператора [6], позволяющее определить:
- числовые характеристики управляющих воздействий как непрерывного, дискретного, импульсного процессов;
- коэффициенты когерентности, полученные по спектральным характеристикам;
- информационная значимость сигналов при формировании управляющих воздействий.
Пример оценки деятельности оператора по управлению объектом с использованием специально разработанных функционалов подробно рассматривается в [4]. Здесь же предлагается методика объективной оценки качества самого объекта управления с использованием функционалов, разработанных для каждого канала управления в отдельности. Что касается интегральных характеристик управления, то они определяются на основе аддитивного глобального критерия (построенного на основе поканальных критериев с учетом межканальной корреляции).
Математическое моделирование в задачах хирургического лечения миопии. В последнее время широко используются хирургические методы коррекции близорукости или дальнозоркости (определяются расположением фокуса хрусталика относительно сетчатки глаза), основанные на математическом моделировании напряженно-деформированного состояния хрусталика (одновременный учет индивидуальных особенностей, например, отсутствие или наличие осевой симметрии, астигматизма и др. невозможен). Поэтому предполагается осевая симметрия роговицы с идентичными меридиональными сечениями роговицы (рис. 1).
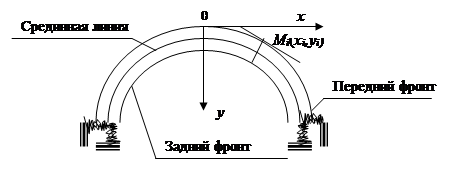
Рис. 1.
Для определения деформаций воспользуемся уравнением срединной линии. Для этого с помощью рефрактометра в точках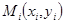 
, лежащих на роговой оболочке, находятся радиусы кривизны. Приближенные значения радиусов кривизны 
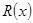на участке 
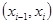определятся в виде
, 
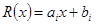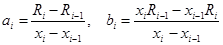
(экспериментальные значения определяются рефрактометром).
Передний фронт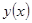 
будет решением ряда задач Коши при различных начальных условиях:
;
, 
;
;
; 
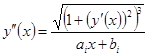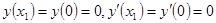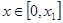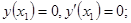
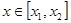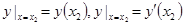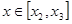
и т. д. Задний фронт оболочки определится по экспериментальным значениям толщины роговицы (используется корнеометр) в точке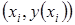 
переднего фронта; срединная линия меридионального сечения роговицы определится по уравнениям фронтов.
Машинная диагностика бредовых психозов. Решение задачи возможно с использованием байесовского подхода (последовательный анализ Вальда). Для вероятностей состояний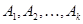 
с симптомами 
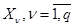(могут быть и зависимыми) справедливо:
.
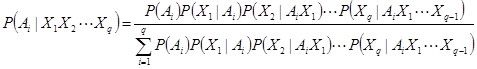Отношение
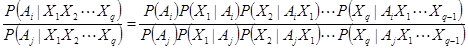
показывает, во сколько состояние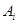 
вероятнее состояния 
.
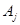Информационная значимость симптомов может быть определена и методами ранговой корреляции.
Количество используемых симптомов определяется по допустимым уровням диагностических ошибок.
При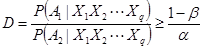 
— состояние 
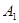; состояние 
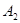при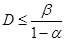 
.
Последовательная процедура продолжается, если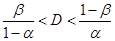 
[7,8].
Указанные результаты использовались для оценки психофизиологического статуса человека-оператора эргатической системы.
Приведенные примеры с очевидностью показывают важность формирования когнитивной компетентности при математическом моделировании сложных систем различной природы для решения задач, как синтеза, так и анализа. Подробный пример использования когнитивной карты (орграфа) дается в [1,2].
Литература:
1. Гарькина И. А., Данилов А. М., Королев Е. В. Когнитивное моделирование при синтезе композиционных материалов как сложных систем / Известия высших учебных заведений. Строительство. — 2009. — № 3–4. — С. 30–37.
2. Гарькина И. А., Данилов А. М., Королев Е. В. Когнитивное моделирование сложных слабоструктурированных систем: пример реализации / Региональная архитектура и строительство. — 2008. — № 2.- С. 16–21.
3. Гарькина И. А., Данилов А. М., Смирнов В. А. Флокуляция в дисперсных системах / Системы управления и информационные технологии. — 2008. — № 2.3(32). — С.344–347.
4. Гарькина И. А., Данилов А. М., Домке Э. Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). –2011. — № 2. — С. 18–23.
5. Авиационные тренажеры модульной архитектуры: монография; под редакцией Лапшина Э. В., д.т.н., проф. Данилова А. М. — Пенза, ИИЦ ПГУ. — 2005. — 146 с.
6. Данилов А. М., Домке Э. Р., Гарькина И. А. Формализация оценки оператором характеристик объекта управления / Информационные системы и технологии.– 2012. — № 2 (70). –С.5–11.
7. Данилов А. М., Гарькина И. А. Теория вероятностей и математическая статистика с инженерными приложениями: допущено УМО ВУЗов РФ по образованию в области транспортных машин и транспортно-технологических комплексов в качестве учебного пособия. — Пенза: ПГУАС. — 2010. — 228 с.
8. Гарькина И. А., Данилов А. М. Специальные разделы высшей математики: учебное пособие. — Пенза: ПГУАС. — 2014. — 160 с.
