В работе представлен пакет расширения, реализованный авторами в рамках системы Mathematica и предназначенный для исследования модели безопасности Белла-ЛаПадулы. Приведено описание функций и команд, используемых в данном пакете.
Введение
Модели безопасности компьютерных систем — это политики безопасности, выраженные формальными способами, например, математически, алгоритмически или схемотехнически [1]. В данной статье рассматривается одна из классических моделей безопасности — мандатная модель Белла-ЛаПадулы [2]. Мы описываем библиотеку подпрограмм для исследования указанной модели, разработанную нами средствами системы компьютерной алгебры Wolfram Mathematica [4]. Библиотека представляет так называемый пакет расширения, дополняющий стандартный функционал среды Mathematica.
Авторы считают, что интеграция данного пакета расширения в образовательный процесс позволит организовать современный учебный материал, обеспечивающий студентов инструментарием самообучения и самоконтроля, позволит проводить интерактивные занятия с визуализацией разных сценариев работы модели Белла-ЛаПадулы. Кроме того, разработанный нами пакет может быть также использован и в научных исследованиях, например, для моделирования процессов передачи прав пользователей в компьютерных системах.
1. Описание модели Белла-ЛаПадулы
Напомним основные положения классической модели Белла-ЛаПадулы [1, 2, 3].
В рамках модели Белла-ЛаПадулы компьютерная система представляется совокупностью следующих компонент:
- множеством объектов доступа O;
- множеством субъектов доступа S;
- множеством прав доступа R = {read, write};
- матрицей доступа A, строки которой отвечают субъектам доступа, а столбцы — объектам доступа. Элементы матрицы доступов — это подмножества множества прав: A [s,o] Í R, s Î S, o Î O;
- линейно упорядоченным множеством L, элементы которого есть уровни безопасности субъектов и объектов доступа;
- функцией F: S È O ® L; данная функция сопоставляет субъектам и объектам доступа некоторые уровни безопасности;
- множеством V состояний системы, которое есть множество всевозможных упорядоченных пар (F, A);
- набора запросов Q субъектов на доступ к объектам, выполнение которых переводит систему в новое состояние;
- функции переходов T: V × Q ® V.
Вводятся следующие определения безопасности состояния системы.
Определение 1. Состояние v Î V называется просто безопасным, если для любых
s Î S и o Î O выполняется условие: read Î A [s, o] Þ F(s) ³ F(o).
Определение 2. Состояние v Î V называется *-безопасным, если для любых s Î S и o Î O выполняется условие: write Î A [s, o] Þ F(o) ³ F(s).
Определение 3. Состояние v Î V называется безопасным, если оно просто безопасное и *-безопасное одновременно.
Определение 4. Система является безопасной, если ее начальное состояние v0 Î V безопасно, и все состояния, достижимые из начального с помощью применения конечной последовательности запросов из множества Q, являются также безопасными.
На основе данных определений Дэвидом Беллом и Леонардом ЛаПадулой была доказана следующая теорема.
Теорема (основная теорема безопасности).
Система является безопасной, если и только если:
1. безопасным является начальное состояние v0 Î V;
2. если v = (F, A) Î V — состояние, достижимое из v0, и v* = T(v, q), где q Î Q,
3. v* = (F*, A*), то для любых s Î S и o Î O выполняются условия:
- если read Î A* [s, o] и read Ï A [s, o], то F*(s) ³ F*(o);
- если read Î A [s, o] и F*(s) < F*(o), то read Ï A* [s, o];
- если write Î A* [s, o] и write Ï A [s, o], то F*(o) ³ F*(s);
- если write Î A [s, o] и F*(o) < F*(s), то write Ï A* [s, o].
2. Реализация модели Белла-ЛаПадулы в рамках системы компьютерной алгебры Mathematica
В настоящее время наряду с программами на различных языках программирования большую популярность в научных исследованиях приобрели системы компьютерной алгебры, ориентированные на проведение сложных символьных вычислений. Наиболее известными на сегодняшний день среди подобных систем являются MATLAB, Mathcad, Maple и Mathematica.
Спектр задач, решаемых подобными системами, очень широк. В частности, MATLAB предназначен преимущественно для решения задач технических вычислений. Mathcad — это система компьютерной алгебры класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов. Система Maple предназначена для символьных вычислений, хотя и имеет ряд средств для численного решения задач.
Система компьютерной алгебры Mathematica — универсальная система, которая осуществляет численные и символьные вычисления. Отличительной особенностью данной системы является очень гибкая работа со списками. Действительно, списки относятся к числу базовых структур данной системы [4], что дает явное преимущество по сравнению с другими системами компьютерной алгебры касательно реализации модели Белла-ЛаПадулы.
Исходя из описания модели Белла-ЛаПадулы, изложенного выше, нами была предложена следующая методика реализации данной модели.
Пользователь должен иметь возможность создавать субъекты и объекты, присваивая им уровни доступа и уровни секретности соответственно. Для этого нами реализованы следующие функции CreateSubject [AccessLevel] и CreateObject [SecurityLevel]. Здесь AccessLevel — уровень доступа субъекта, SecurityLevel — уровень секретности объекта. Отметим, что в нашей реализации модели уровни безопасности — это целые числа.
Далее, пользователь должен иметь возможность устанавливать права в ячейках матрицы доступов. Для этого служит функция SetRights [SubjectNumber, ObjectNumber, Rights], где SubjectNumber — списочный номер субъекта, ObjectNumber — списочный номер объекта, Rights — предоставляемые права субъекту на объект (задается списком {1, 2}, где 1 — право на чтение, 2 — право на запись). Указание фигурных скобок в данном параметре обязательно.
В процессе использования реализации модели всегда можно просмотреть текущее состояние системы. Это делается с помощью команды ShowAllList. После выполнения данной команды выводятся матрица доступов, и таблицы с уровнями безопасности субъектов и объектов (пример на рис. 1).
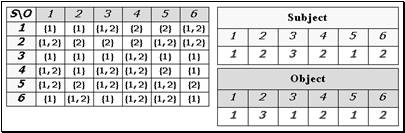
Рис. 1. Текущее состояние системы
Из рисунка видно, что в рамках приведенного нами примера в системе присутствуют 6 субъектов и 6 объектов с соответствующими уровнями безопасности. Каждому субъекту даны некоторые права на объекты.
Проверка безопасности состояния системы осуществляется командами SimpleSecurityQ и StarSecurityQ. Обе эти команды выводят матрицы доступов системы.
На рис. 2 приведен пример вывода команды SimpleSecurityQ. Темно-серым цветом обозначены ячейки, в которых права заданы неправильно, светло-серым — права заданы правильно, не закрашенные ячейки — уровень доступа субъекта выше или равен уровню секретности объекта.
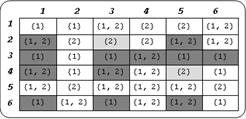
Рис. 2. Простое правило безопасности
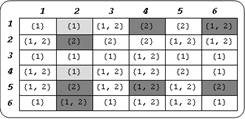
Рис. 3. *-свойство
На рис. 3 приведен пример вывода функции StarSecurityQ. Здесь темно-серым цветом обозначены ячейки, в которых права заданы неправильно, светло-серым — права заданы правильно, не закрашенные ячейки — уровень доступа субъекта ниже или равен уровню секретности объекта.
Описываемый пакет расширения содержит также и ряд дополнительных подпрограмм.
Для удаления субъектов и объектов:RemoveSubject[SubjectNumber] и
RemoveObject [ObjectNumber],где SubjectNumber — списочный номер субъекта,
ObjectNumber — списочный номер объекта.
Для изменения уровней доступа субъектов или уровня секретности объектов: ChangeSubjectLevel [SubjectNumber, AccessLevel] и ChangeObjectLevel [ObjectNumber, SecurityLevel], где AccessLevel — новый уровень доступа субъекта, SecurityLevel — новый уровень секретности объекта.
Для выполнения запросов на изменение состояния системы:
- запрос на возможность получения определенных прав субъектом на объект:
Query [SubjectNumber, ObjectNumber, Right];
- запрос на изменение уровня доступа у субъекта:
QueryChangeAccess [SubjectNumber, AccessLevel];
- запрос на изменение уровня секретности у объекта:
QueryChangeSecurity [ObjectNumber, SecurityLevel].
Кроме того, для учебно-методических целей была добавлена обучающая процедура, задаваемая функцией:
Test [SubjectNumber, ObjectNumber, LevelsNumber],где SubjectNumber– количество субъектов, ObjectNumber — количество объектов, LevelsNumber — количество уровней секретности. В результате выполнения данной команды, на экран выводится окно (рис. 4) содержащее:
- матрицу доступов с пустыми ячейками;
- список субъектов с произвольным заполнением уровней доступа;
- список объектов с произвольным заполнением уровней секретности;
- таблицу заполнения прав доступа;
- кнопку «Проверка заполнения таблицы», справа от которой отображается число нажатий на кнопку.
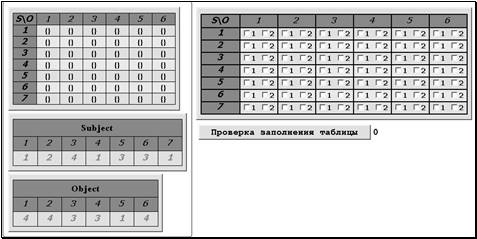
Рис. 4. Режим проверки знаний
Суть данной процедуры в следующем. Придерживаясь основных правил модели Белла-ЛаПадулы (см. теорему) пользователь задает права доступов субъектов на объекты, выставляя соответствующие флаги в таблице. При нажатии на кнопку «Проверка заполнения таблицы» выводится отдельное окно с таблицей результатов (рис. 5). Стоит отметить, что в данном случае проводится полная проверка безопасности системы.
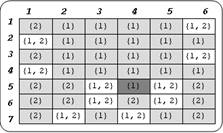
Рис. 5. Результат проверки знаний
Заключение
В настоящей статье описан пакет расширения системы Mathematica, реализующий основные положения модели безопасности Белла-ЛаПадулы. Разработанная библиотека позволяет существенно расширить возможности изучения политик безопасности и повысить уровень и качество обучения студентов по соответствующим дисциплинам.
Литература:
1. Девянин П. Н. Модели безопасности компьютерных систем: Учеб. пособие для вузов. — М.: Академия, 2005. — 144 с.: ил.
2. Bell D. E., La Padula L. J. Secure Computer System: Unified Exposition and Multics Interpretation. Bedford, MA 01730 — March, 1976
3. Зегжда Д. П., Ивашко А. М. Основы безопасности информационных систем. — М.: Горячая линия — Телеком, 2000. — 452 с.
4. Computation meets knowledge. Wolfram Language & System. Documentation Center [Электронный ресурс]. URL: http://reference.wolfram.com/language/







