Численное решение уравнения Пуассона является важным элементом многих задач вычислительной физики.
В данной работе опишем новую вычислительную модель для поиска приближенного решения смешанной краевой задачи для уравнения Пуассона. Данная модель использует нестационарные регуляризации, метод прямых, идеи схем без насыщения, сплайн-интерполяцию, метод прогонки и метод установления (рис. 1).
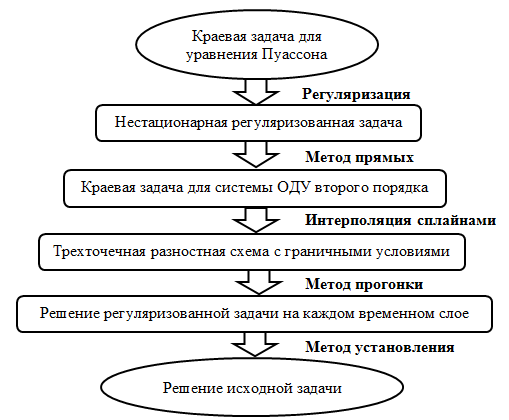
Рис. 1.Алгоритм поиска приближенных решений краевой задачи для уравнения Пуассона
Рассмотрим в прямоугольной области  (см. рис. 2) уравнение Пуассона для функции
(см. рис. 2) уравнение Пуассона для функции 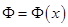 :
:
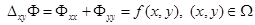 (1)
(1)
со смешанными краевыми условиями:
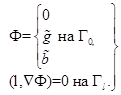 (2)
(2)
Здесь 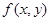 ‒ известная правая часть,
‒ известная правая часть, 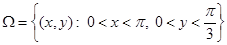 ,
, 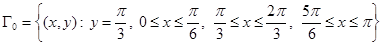 ‒ часть границы
‒ часть границы 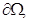
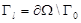 ,
, 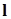 ‒ единичный вектор внешней нормали к границе
‒ единичный вектор внешней нормали к границе 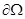 ,
, 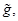
 ‒ некоторые постоянные.
‒ некоторые постоянные.
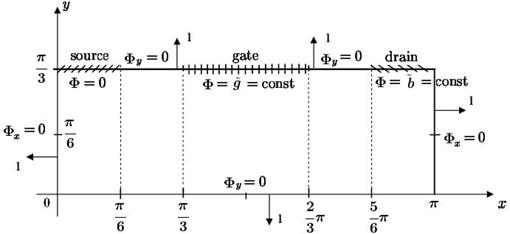
Рис. 2. Область 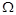 и граница
и граница 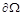 для модельной задачи
для модельной задачи
Замечание. Сделав в задаче (1), (2) замену зависимой переменной  :
:
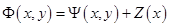 ,
,
где функция 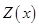 изображена на рис. 3, мы получаем для новой зависимой переменной
изображена на рис. 3, мы получаем для новой зависимой переменной 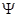 следующую смешанную краевую задачу:
следующую смешанную краевую задачу:
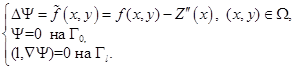
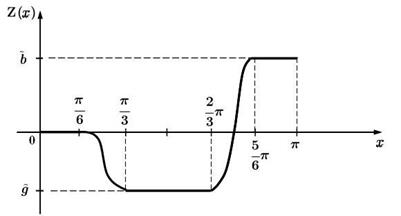
Рис. 3. График вспомогательной достаточно гладкой функции 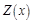
Следовательно, не нарушая общности, будем полагать далее, что в (2) функция  удовлетворяет на
удовлетворяет на 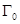 однородному условию
однородному условию  .
.
При конструировании численного алгоритма для нахождения приближенных решений задачи (1), (2) мы воспользуемся методом установления. С этой целью вместо уравнения Пуассона (1) рассмотрим три его нестационарные регуляризации:
1.параболическая регуляризация
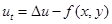 , (3)
, (3)
2. регуляризация Соболева
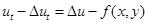 , (4)
, (4)
3.гиперболическая регуляризация
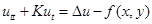 . (5)
. (5)
Здесь 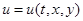 ‒ новая неизвестная функция,
‒ новая неизвестная функция, 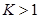 ‒ постоянная,
‒ постоянная, 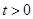 ‒ временная переменная. Краевые условия (2) для уравнений (3 ‒ 5) перепишутся так
‒ временная переменная. Краевые условия (2) для уравнений (3 ‒ 5) перепишутся так
 . (6)
. (6)
Добавляя начальные условия
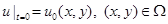 , (7)
, (7)
стационарное решение исходной смешанной краевой задачи ищется как предел 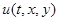 при
при 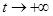 .
.
Для каждого из трех видов регуляризаций получены априорные оценки на нормы решений резуляризованных задач, из которых следует сходимость 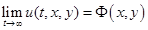 , а также однозначная разрешимость и устойчивость стационарного решения.
, а также однозначная разрешимость и устойчивость стационарного решения.
Для нахождения приближенного решения смешанной задачи (3), (6), (7) или (4), (6), (7) или (5), (6), (7) предложена дифференциально-разностная модель, основанная на методе прямых и принципах схем без насыщения. При этом производную 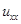 в уравнениях (3) — (5) мы заменим не разностным отношением, а используем для аппроксимации ее интерполяционный многочлен [1]
в уравнениях (3) — (5) мы заменим не разностным отношением, а используем для аппроксимации ее интерполяционный многочлен [1]
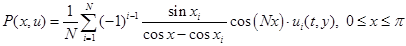
с узлами в нулях многочлена Чебышева
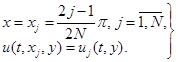
В итоге для каждой из регуляризаций будем иметь:
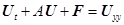 , (8)
, (8)
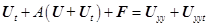 , (9)
, (9)
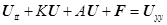 , (10)
, (10)
где 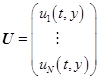 ,
, 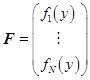 ,
, 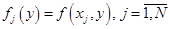 ,
, 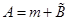 ,
, 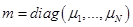 ,
, 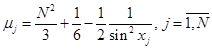 ,
, 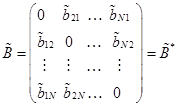 ,
, 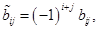
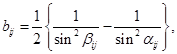
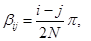
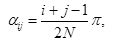
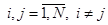 .
.
Далее в системах (8) ‒ (10) проведем дискретизацию по переменной 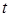 . С этой целью вводим обозначения:
. С этой целью вводим обозначения: 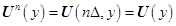 ,
, 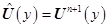 ,
, 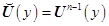 ,
, 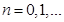 ,
,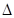 ‒ шаг разностной сетки по времени.
‒ шаг разностной сетки по времени.
Заменяя 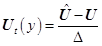 ,
, 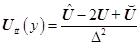 получаем систему ОДУ второго порядка:
получаем систему ОДУ второго порядка:
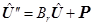 (11)
(11)
Выражения для элементов матрицы 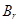 и компонент вектора
и компонент вектора 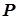 зависят от вида примененной регуляризации:
зависят от вида примененной регуляризации:
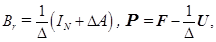
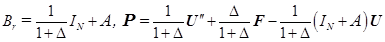 ,
,
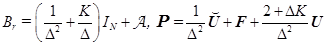 ,
,
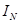 ‒ единичная матрица порядка N.
‒ единичная матрица порядка N.
К системе (11) добавляем граничные краевые условия (см. (6)):
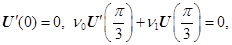 (12)
(12)
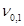 -диагональные матрицы порядка N(диагональные элементы равны либо 0, либо 1), причем:
-диагональные матрицы порядка N(диагональные элементы равны либо 0, либо 1), причем: 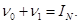
Учитывая определенные трудности, возникающие при практическом использовании формулы для нахождения приближенного решения краевой задачи (11), (12), мы предложим следующую технологию построения приближенного решения этой краевой задачи. Будем искать приближенное решение в виде интерполяционного кубического сплайна класса 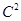 (см. [2]):
(см. [2]):
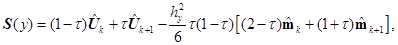 (13)
(13)
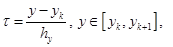
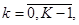
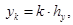
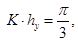
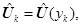
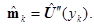
С учетом (13) из (11), (12) получаем трехточечную разностную схему:
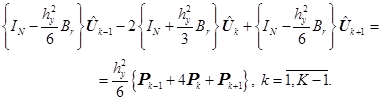 (11)
(11)
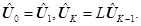
Здесь 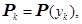
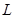 ‒ диагональная матрица порядка N (диагональные элементы равны либо 0, либо 1). Систему алгебраических уравнений (11) можно решить методом матричной прогонки. Из неравенства
‒ диагональная матрица порядка N (диагональные элементы равны либо 0, либо 1). Систему алгебраических уравнений (11) можно решить методом матричной прогонки. Из неравенства 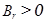 следуют условия хорошей обусловленности разностной краевой задачи (11).
следуют условия хорошей обусловленности разностной краевой задачи (11).
Данный алгоритм был запрограммирован на языке Object Pascal (среда Delphi 6). Были проведены тестовые расчеты, которые показали хорошую работоспособность, приведенного выше алгоритма.
Данный алгоритм хорошо зарекомендовал себя при поиске решения 1D задачи о баллистическом диоде и 2D задачах о переносе заряда в транзисторе MESFET и MOSFET.
Литература:
1. Бабенко К. И. Основы численного анализа. Москва-Ижевск: НИЦ " Регулярная и хаотическая динамика», 2002.
2. Завьялов Ю. С., Квасов Б. И., Мирошниченко В. Л. Методы сплайн ‒ функций. М.: Наука, 1980.







