Пусть 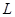 — минимальный замкнутый симметрический оператор, порожденный формально самосопряженным дифференциальным выражением
— минимальный замкнутый симметрический оператор, порожденный формально самосопряженным дифференциальным выражением
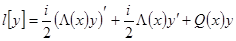 (1)
(1)
в гильбертовом пространстве 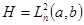 вектор-функций
вектор-функций 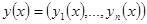 , рассматриваемых как вектор-столбцы, со скалярным произведением
, рассматриваемых как вектор-столбцы, со скалярным произведением
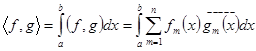 .
.
Коэффициенты 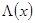 и
и 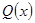 выражения (1) — эрмитовы матрицы-функции, причем
выражения (1) — эрмитовы матрицы-функции, причем 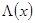 невырождена и абсолютно непрерывна на
невырождена и абсолютно непрерывна на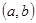 ;
; 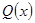 суммируема на любом сегменте
суммируема на любом сегменте 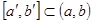 . Пусть
. Пусть 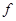 и
и 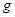 — вектор-функции, для которых выражение (1) имеет смысл. Тогда имеет место аналог тождества Лагранжа:
— вектор-функции, для которых выражение (1) имеет смысл. Тогда имеет место аналог тождества Лагранжа:
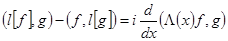 . (2)
. (2)
С помощью стандартных рассуждений (см. например, [1]) можно показать, что максимальный оператор, порожденный в пространстве 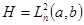 дифференциальным выражением (1), является сопряженным оператору
дифференциальным выражением (1), является сопряженным оператору 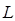 . Обозначим его символом
. Обозначим его символом 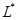 . Принимая во внимание тождество (2), область определения
. Принимая во внимание тождество (2), область определения 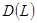 оператора
оператора 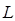 можно охарактеризовать как линейное многообразие тех вектор-функций
можно охарактеризовать как линейное многообразие тех вектор-функций 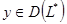 , которые для любой вектор-функции
, которые для любой вектор-функции 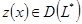 удовлетворяют условию
удовлетворяют условию 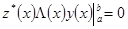 .
.
В этой работе исследуется кратность спектра самосопряженного расширения 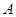 оператора
оператора 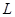 , порожденного операцией
, порожденного операцией 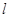 в гильбертовом пространстве
в гильбертовом пространстве 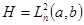 .
.
Стандартным образом (cм., например, [1]) можно построить обобщенную резольвенту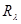 оператора
оператора 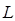 , которая при любом невещественном
, которая при любом невещественном 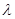 является интегральным оператором вида
является интегральным оператором вида 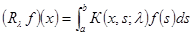 , где
, где 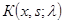 — матричное ядро
— матричное ядро
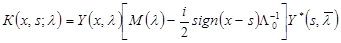 ,
,
а 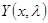 — фундаментальная матрица однородной системы
— фундаментальная матрица однородной системы 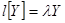 , удовлетворяющая условию
, удовлетворяющая условию 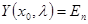 (
(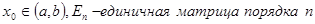 );
); 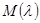 — характеристическая матрица-функция оператора
— характеристическая матрица-функция оператора 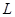 ;
; 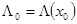 . Обобщенная резольвента
. Обобщенная резольвента 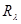 — симметрического оператора
— симметрического оператора 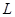 допускает представление вида
допускает представление вида 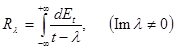 , где
, где 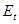 обобщенная спектральная функция оператора
обобщенная спектральная функция оператора 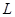 . Положим
. Положим
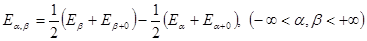 .
.
При помощи формулы обращения Стилтьеса спектральная функция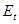 однозначно восстанавливается по соответствующей ей обобщенной резольвенте. Для любых вектор-функций
однозначно восстанавливается по соответствующей ей обобщенной резольвенте. Для любых вектор-функций 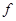 и
и 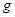 из
из 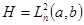 и любых вещественныx
и любых вещественныx 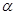 и
и 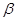 имеет место равенство:
имеет место равенство:
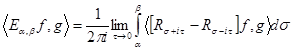 ,
,
позволяющее получить формулу всех спектральных функций 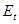 оператора
оператора 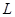 :
:
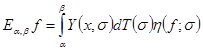 , (3)
, (3)
где 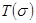 — спектральная матрица-функция распределения оператора
— спектральная матрица-функция распределения оператора 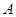 ,
, 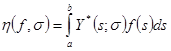 .
.
Подпространство 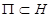 называется порождающим подпространством самосопряженного оператора
называется порождающим подпространством самосопряженного оператора 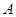 со спектральной функцией
со спектральной функцией 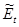 , если замыкание линейной оболочки множества
, если замыкание линейной оболочки множества 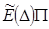 , где
, где 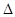 пробегает совокупность всех интервалов числовой оси, совпадает с
пробегает совокупность всех интервалов числовой оси, совпадает с 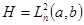 . Кратностью спектра самосопряженного оператора
. Кратностью спектра самосопряженного оператора 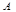 называется минимальная размерность порождающего подпространства этого оператора.
называется минимальная размерность порождающего подпространства этого оператора.
Известно (cм., например, [2, 3]), что совокупность всех обобщенных резольвент 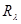 симметрического оператора
симметрического оператора 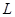 в гильбертовом пространстве
в гильбертовом пространстве 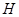 определяется формулой
определяется формулой 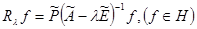 , где
, где 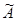 — любое самосопряженное расширение оператора
— любое самосопряженное расширение оператора 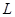 в некотором объемлющем пространстве
в некотором объемлющем пространстве 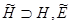 — единичный оператор в
— единичный оператор в 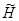 , а
, а 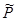 — оператор проектирования в
— оператор проектирования в 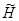 на
на 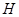 . Введем обозначения:
. Введем обозначения: 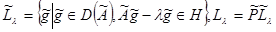 . Тогда имеет место
. Тогда имеет место
Лемма 1. Пусть 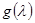 — вектор-функция, удовлетворяющая условиям:
— вектор-функция, удовлетворяющая условиям: 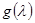 представима в виде
представима в виде 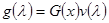 , где
, где 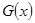 — квадратная матрица, столбцами которой служат вектор-функции
— квадратная матрица, столбцами которой служат вектор-функции 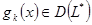 , а
, а 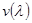 — вектор-функция, удовлетворяет условию Липшица. Кроме того, при любом
— вектор-функция, удовлетворяет условию Липшица. Кроме того, при любом 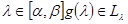 .
.
Тогда для любого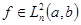 и любого
и любого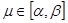 имеет место равенство
имеет место равенство
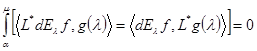 , (4)
, (4)
где 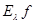 определяется формулой (3).
определяется формулой (3).
Соотношения (2) и (4) приводят к следующей лемме.
Лемма 2. Пусть при любом 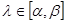 система уравнений
система уравнений 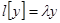 имеет решение
имеет решение 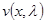 такое, что;
такое, что;
1. 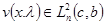 , где
, где 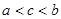 ;
;
2. для любой вектор-функции 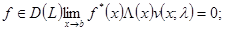
3. при фиксированном 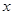 вектор-функция
вектор-функция 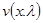 удовлетворяет условию Липшица относительно
удовлетворяет условию Липшица относительно 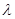 на сегменте
на сегменте 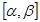 . Тогда при любых
. Тогда при любых 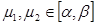
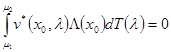 ,
,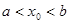 (5)
(5)
Теорема 1. Пусть при любом 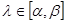 система
система 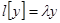 имеет
имеет 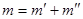 линейно независимых решений
линейно независимых решений
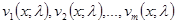 (6)
(6)
таких, что:
1. для каждого из 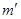 первых решений (6) выполняются условия:
первых решений (6) выполняются условия:
а) 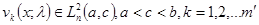 ;
;
б) для любой вектор-функции 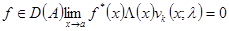 ;
;
2. для каждого из 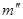 последних решений (6) выполняются условия:
последних решений (6) выполняются условия:
а) 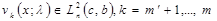 ;
;
б) для любой вектор-функции 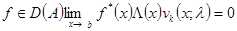 ;
;
3. каждая из вектор-функций (6) при фиксированном 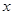 удовлетворяет условию Липшица относительно
удовлетворяет условию Липшица относительно 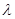 на сегменте
на сегменте 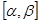 .
.
Тогда кратность части спектра самосопряженного расширения 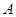 оператора
оператора 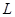 , заключенной в сегменте
, заключенной в сегменте 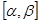 , не превосходит
, не превосходит 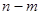 .
.
При доказательстве теоремы существенно используется соотношение (5).
Замечание. Если оператор 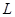 с минимальной областью определения, порожденный операцией
с минимальной областью определения, порожденный операцией 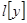 в пространстве
в пространстве 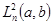 является самосопряженным, то условия 1. б и 2. б можно опустить. В частности, такая ситуация складывается, если выполняются условия
является самосопряженным, то условия 1. б и 2. б можно опустить. В частности, такая ситуация складывается, если выполняются условия
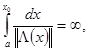
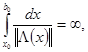
Пусть конец 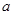 промежутка
промежутка 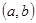 регулярен. Как известно, самосопряженное расширение
регулярен. Как известно, самосопряженное расширение 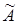 в
в 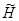 симметрического оператора
симметрического оператора 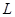 называют минимальным, если подпространство
называют минимальным, если подпространство 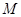 , такое что
, такое что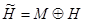 , и ни одно его подпространство, отличное от нулевого пространства не приводит
, и ни одно его подпространство, отличное от нулевого пространства не приводит 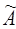 . Имеет место теорема 2.
. Имеет место теорема 2.
Теорема 2. Пусть сегмент 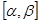 не содержит собственных значений оператора
не содержит собственных значений оператора 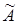 и при любом
и при любом 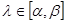 система уравнений
система уравнений 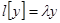 имеет
имеет 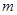 линейно независимых решений
линейно независимых решений 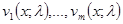 таких, что:
таких, что:
1. 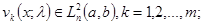
2. для каждой вектор-функции 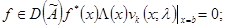
3. каждая из вектор-функций 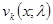 при фиксированном
при фиксированном 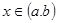 удовлетворяет условию Липшица относительно
удовлетворяет условию Липшица относительно 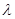 на сегменте
на сегменте 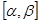 . Тогда кратность непрерывной части спектра оператора
. Тогда кратность непрерывной части спектра оператора 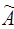 , заключенной в сегменте
, заключенной в сегменте 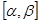 не превосходит
не превосходит 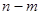 .
.
Теоремы 1 и 2 позволяют судить о характере спектра самосопряженных расширений оператора 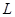 на основе поведения коэффициентов дифференциального выражения (1) в окрестности сингулярных концов промежутка
на основе поведения коэффициентов дифференциального выражения (1) в окрестности сингулярных концов промежутка 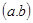 .
.
Введем обозначения: 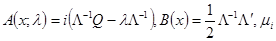 - собственные значения матрицы
- собственные значения матрицы 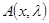 .
. 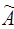 минимальное самосопряженное расширение оператора
минимальное самосопряженное расширение оператора 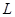 , порожденного выражением (1) в пространстве
, порожденного выражением (1) в пространстве 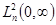 . Предположим, что
. Предположим, что 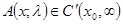 при
при 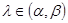 и
и 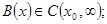 число
число 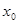 можно брать произвольно большим.
можно брать произвольно большим.
Теорема 3. Пусть при любом 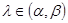 матрицы
матрицы 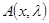 и
и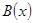 , таковы, что:
, таковы, что:
1. матрица 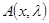 имеет конечный предел на бесконечности
имеет конечный предел на бесконечности 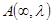 , причем предельная матрица имеет различные собственные значения;
, причем предельная матрица имеет различные собственные значения;
2. матрицы 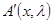 и
и 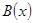 абсолютно интегрируемы на промежутке
абсолютно интегрируемы на промежутке 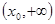 ;
;
1. собственные значения матрицы 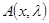 просты, отличны от нуля и асимптотически разделены, т. е.
просты, отличны от нуля и асимптотически разделены, т. е. 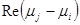 не равно нулю для различных индексов.
не равно нулю для различных индексов.
Тогда кратность непрерывной части спектра оператора 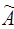 , содержащейся в сегменте
, содержащейся в сегменте 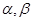 не превосходит
не превосходит 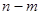 , где
, где 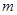 число собственных значений матрицы
число собственных значений матрицы 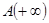 , лежащих в левой полуплоскости.
, лежащих в левой полуплоскости.
Теорема 4. Пусть при любом 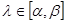 :
:
1. матрицы 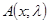 и
и 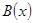 согласованы, т. е.
согласованы, т. е. 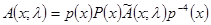 и
и 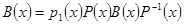 , где
, где 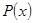 — диагональная матрица с элементами
— диагональная матрица с элементами 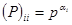 (
(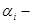 постоянные),
постоянные), 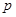 и
и 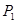 — комплекснозначные функции,
— комплекснозначные функции, 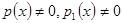 для
для 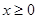 ;
;
2. матрица 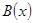 подчинена матрице
подчинена матрице 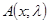 при
при 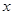 намного большем, чем единица, т. е.
намного большем, чем единица, т. е. 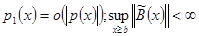 ;
;
3. предел 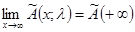 существует и конечен, матрица
существует и конечен, матрица 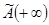 невырождена и имеет различные собственные значения
невырождена и имеет различные собственные значения 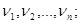
4. 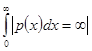 и
и 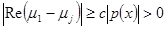 при
при 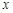 намного большем, чем единица;
намного большем, чем единица;
5. 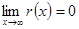 , где
, где 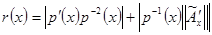 . Тогда кратность непрерывной части спектра оператора
. Тогда кратность непрерывной части спектра оператора 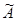 , содержащейся в сегменте
, содержащейся в сегменте 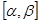 не превосходит
не превосходит 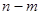 , где
, где 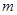 - число собственных значений матрицы
- число собственных значений матрицы 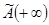 , удовлетворяющих условию
, удовлетворяющих условию 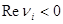 .
.
Литература:
1. Наймарк М. А. Линейные дифференциальные операторы. М., Наука, 1969.
2. Фетисов В. Г., Филиппенко В. И. Исследования по теории операторов и их приложениям. Монография. Шахты: Изд-во ЮРГУЭС, 2008. — 185 с.
3. Филиппенко В. И. Линейные квазидифференциальные операторы в гильбертовом пространстве //Исследования по функциональному анализу и его приложениям. — М.: Наука, 2006. С. 293–344.







