Известно, что одним из способов повышения качества обучения математике является применение в образовательном процессе методов, способствующих развитию и становлению познавательной активности и самостоятельности обучаемых. Одним из таких методов является метод наглядности.
В педагогической и методической литературе уделяется большое внимание принципу наглядности в обучении. Роль наглядности и её значение рассматривается в работах Я. А. Коменского, А. Н. Леонтьева, Г.Пестоллоци, К. Д. Ушинского, Л. М. Фридмана и др. В них особо отмечается важность применения наглядности в обучении математике, в связи с тем, что математика способствует развитию логического мышления, пространственного воображения.
В обучении математике широко применяется символическая наглядность, основу которой составляют чертежи, графики, схемы, таблицы. Наглядные пособия в процессе обучения математике используют для ознакомления с новым материалом, для формирования знаний, умений, навыков, для проверки уровня их усвоения.
При изучении дифференциальных уравнений в курсе математического анализа у студентов возникают большие трудности с их решением, особенно когда в задании не указано какое уравнение требуется решить. Студент должен сам определить вид уравнения и вспомнить метод его решения. Для овладения методами решения дифференциальных уравнений первого порядка составляется вспомогательная таблица (таблица 1), которая является опорным конспектом по данной теме.
Таблица 1
Дифференциальные уравнения первого порядка
|
Название уравнения |
Вид уравнения |
Метод интегрирования |
|
1. С разделенными переменными |
|
|
|
2. С разделяющимися переменными |
|
|
|
3. Приводящиеся к уравнению с разделяющимися переменными |
а) |
а) подстановка
|
|
б) |
б) подстановка
|
|
|
4. Линейные относительно |
|
а) метод Лагранжа б) метод Бернулли: |
|
5. Уравнение Бернулли |
|
Метод Бернулли: |
|
6. Однородные |
а) б)
|
Подстановка |
|
7. Приводящиеся к однородному |
|
|
|
8. В полных дифференциалах |
|
|
|
9. Приводящиеся к уравнению в полных дифференциалах |
а) б) |
а) б)
(см.8) |
Также большие трудности у студентов вызывает решение линейных неоднородных дифференциальных уравнений с постоянными коэффициентами. Для помощи студентам в освоении методики их решения составляется таблица соответствия вида частного решения виду правой части (таблица 2).
Таблица 2
Соответствие вида частного решение виду правой части ЛНДУ
|
Вид правой части |
|
Вид частного решения |
|
1. |
а)
б) |
а)
б)
|
|
2. |
а)
б) |
а)
б)
|
|
3. |
а)
б) |
а) А и В — постоянные неопределенные коэффициенты б) |
|
4.
|
а)
б) |
а)
б)
|
Приведенные выше таблицы можно применять на различных этапах обучения решению дифференциальных уравнений, особенно они помогают студентам в самостоятельной работе.
Применение наглядности при обучении математике активизирует мыслительную деятельность, повышая уровень усвоения основных математических понятий и качество математической подготовки студентов, являющейся основой их профессиональной подготовки.
Литература:
1. Гудкова В. С., Ячинова С.Н, Новичкова Т. Ю. Наглядность как средство повышения качества обучения математике // Вестник магистратуры. — 2014. — № 12–4 (39). — С.41–43.
2. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Построение математических моделей в прикладных задачах // Молодой ученый. — 2013. — № 12 (59). — С. 3–6.
3. Куимова Е. И., Куимова К. А., Ячинова С. Н. Формирование мотивационной составляющей обучения на примере изучения дифференциальных уравнений // Молодой ученый. — 2014. — № 2(61) — с.775–777.
4. Новичкова Т. Ю., Крымская Ю. А., Ячинова С. Н. Прикладная направленность преподавания математики как средство повышения качества обучения в военных вузах // Молодой ученый. — 2014. — № 18. — С. 619–621.
5. Ячинова С. Н., Гудкова В. С. Мотивация обучения студентов посредством моделирования // Молодой ученый. — 2014. — № 4 — с.1141–1144.







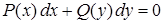
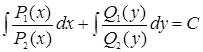
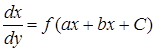 ;
;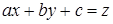
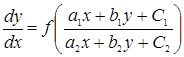 , если
, если 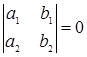
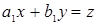
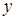
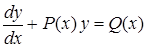
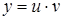
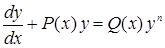
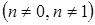
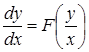 ;
;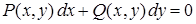
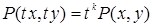
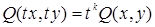
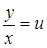
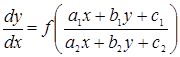 , если
, если 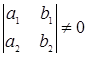
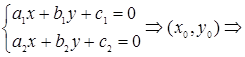
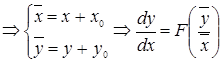
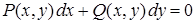 ,
,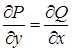
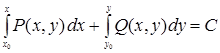
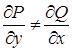 , но
, но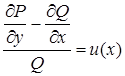
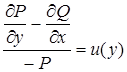
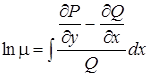
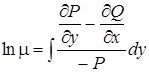
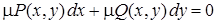
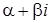
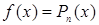 ,
, 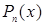 — многочлен степени n от х.
— многочлен степени n от х.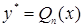 ,
,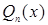 -многочлен той же степени, что и
-многочлен той же степени, что и 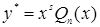 ,
,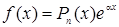 ,
, 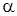 - не корень характеристического уравнения
- не корень характеристического уравнения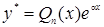 ,
,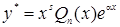 ,
,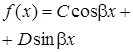 , С,D — постоянные числа
, С,D — постоянные числа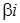 - не корень характеристического уравнения
- не корень характеристического уравнения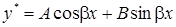 ,
,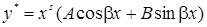 А и В — постоянные неопределенные коэффициенты
А и В — постоянные неопределенные коэффициенты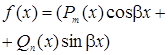 ,
, 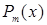 - многочлен степени m,
- многочлен степени m,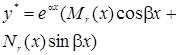
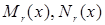 -многочлены степени r, r=max(m,n)
-многочлены степени r, r=max(m,n)