Разработка вероятностных моделей является очень актуальной задачей в наше время. В большей части литературы по актуарной математики описываются модели, рассчитанные на однородный портфель договоров страхования. [1]. Но наиболее распространённый случай неоднородного портфеля до сих пор остается недостаточно изученным. Поэтому в данной работе изучается модель неоднородного портфеля договоров. Для решения данной задачи был использован специальный комбинаторный аппарат. Был получен явный вид распределения для числа поданных исков. Так же был рассмотрен случай, когда в неоднородном портфеле договоров выплатой является случайная величина, равномерно распределенная на отрезке. Получен явный вид закона распределения и формулы для числовых характеристик.
Обобщенные числа Стирлинга первого рода и их некоторые свойства
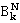 — обобщенные числа Стирлинга первого рода, N=0, 1, …; k=0,1, ….
— обобщенные числа Стирлинга первого рода, N=0, 1, …; k=0,1, ….
Пусть 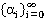 - база (одномерная последовательность вырожденной матрицы весов). Полагаем, что ее члены принимают значения из некоторого числового поля.
- база (одномерная последовательность вырожденной матрицы весов). Полагаем, что ее члены принимают значения из некоторого числового поля.
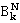 — это сумма всех различных произведений по N-k сомножителей, которые выбираются без повторений из N первых членов базы. Полагаем
— это сумма всех различных произведений по N-k сомножителей, которые выбираются без повторений из N первых членов базы. Полагаем 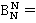 1 и
1 и 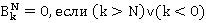 .
.
Приведем значения некоторых чисел. Получаем
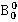 =1;
=1;
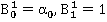 ;
;
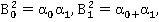
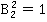 ;
;
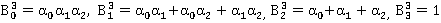 ;
;
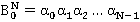 .
.
Введем рекуррентное соотношение для рассматриваемых комбинаторных чисел.
В сумме произведений членов базы, выражающей 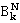 , сгруппируем слагаемые, не содержащие множитель
, сгруппируем слагаемые, не содержащие множитель 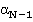 ; в совокупности они образуют
; в совокупности они образуют 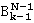 . Из суммы остальных слагаемых выделяем общий множитель
. Из суммы остальных слагаемых выделяем общий множитель 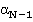 , то, что остается после выделения, есть
, то, что остается после выделения, есть 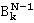 . В результате получаем
. В результате получаем
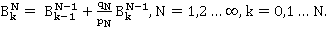 [2] (1)
[2] (1)
Рассмотрим производящие функции для множеств числа 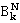 , N=0,1…; k=0,1..N. Поскольку описываемое число зависит от двух индексов, изменяющихся в вышеуказанных пределах, в общем виде это будет функция, производящая бесконечные треугольные матрицы:
, N=0,1…; k=0,1..N. Поскольку описываемое число зависит от двух индексов, изменяющихся в вышеуказанных пределах, в общем виде это будет функция, производящая бесконечные треугольные матрицы:
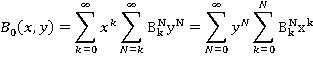
Начнем с более простых частных случаев, когда один из индексов фиксирован.
При фиксированном натуральном N рекуррентное выражение (1) почленно умножаем на 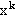 и полученное суммируем по k в пределах от 0 до N. Имеем
и полученное суммируем по k в пределах от 0 до N. Имеем
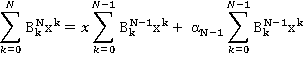
Пусть
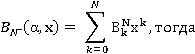
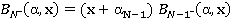 .
.
Применяя последнюю формулу N раз, находим
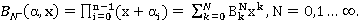 (2)
(2)
С учетом формулы (2.3.2.) общая производящая функция обобщенного числа Стирлинга первого рода запишется в следующем виде [2]:
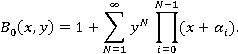
Постановка задачи Пусть имеется N договоров страхования и предполагается выполнение условий:
- каждый договор заключается на определенный период;
- в течение данного периода новые договоры не заключаются;
- по любому договору может быть подан лишь один иск.
Портфель договоров страхования бывает двух видов: однородный и неоднородный. Случай однородного портфеля изучен достаточно хорошо. Случай неоднородного портфеля является менее изученным, но наиболее интересным.
Будем изучать распределения случайных величин 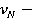 число поданных исков по портфелю за рассматриваемый период и ξ — размер иска по одному договору.
число поданных исков по портфелю за рассматриваемый период и ξ — размер иска по одному договору.
Примером неоднородного портфеля является страхование жизни, ведь для каждой возрастной категории вероятность наступления страхового случая своя. Для нахождения распределения величины 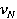 воспользуемся так называемой В-схемой последовательных испытаний. [1] Пусть проводится N испытаний типа «успех-неуспех», и вероятность успеха может меняться после каждого испытания. В этом случае число успехов в N испытаниях имеет распределение
воспользуемся так называемой В-схемой последовательных испытаний. [1] Пусть проводится N испытаний типа «успех-неуспех», и вероятность успеха может меняться после каждого испытания. В этом случае число успехов в N испытаниях имеет распределение
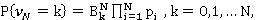 (2.1)
(2.1)
где 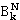 -обобщенные числа Стирлинга первого рода, построенные на базе
-обобщенные числа Стирлинга первого рода, построенные на базе 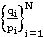 .
.
Разобьем портфель договоров на L однородных групп. Вероятность наступления страхового случая в первой группе равна 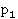 , во второй
, во второй 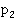 ,.., в группе под номером L
,.., в группе под номером L 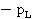 .
.
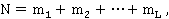
где 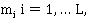 — число элементов в соответствующей группе.
— число элементов в соответствующей группе.
По каждому договору страхования иск может быть предъявлен не более одного раза. Максимальное число поданных исков равно N. Вероятности наступления страхового случая, соответствующие каждому договору, имеют вид: 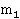 вероятностей типа
вероятностей типа 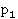 ,
, 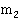 вероятностей типа
вероятностей типа 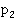 , …,
, …, 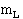 вероятностей типа
вероятностей типа 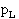 .
.
В рассмотренных выше условиях формула (2.1.) примет вид:
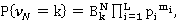 (2.2)
(2.2)


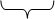 где
где 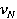 - число исков, поданных в рассматриваемый период, а базой для обобщенных чисел Стирлинга первого рода является набор
- число исков, поданных в рассматриваемый период, а базой для обобщенных чисел Стирлинга первого рода является набор
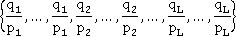
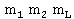
С помощью представления (2.2.) можно изучать свойства распределений, находить его характеристики и исследовать асимптотику.
Предположим теперь, что портфель из N договоров разбит, как и ранее, на L групп, причем вероятность наступления страхового случая по каждому договору одна и та же и равна p, а величина выплаты по договору из i-ой группы имеет распределение, равномерное на 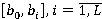 , если страховой случай был. Требуется найти закон распределения размера иска ξ по наудачу выбранному договору. Заметим, что возможно представление ξ=I*η, где I- индикатор события, означающего наличие страхового случая по данному договору:
, если страховой случай был. Требуется найти закон распределения размера иска ξ по наудачу выбранному договору. Заметим, что возможно представление ξ=I*η, где I- индикатор события, означающего наличие страхового случая по данному договору:
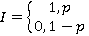 ,
,
где р — вероятность наступления страхового случая;
η- величина выплаты по наудачу выбранному договору, если страховой случай был.
Найдены функция плотности вероятности и функция распределения величины η:
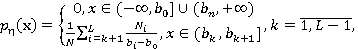 (3.1.)
(3.1.)
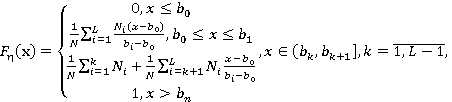 (3.2.)
(3.2.)
Это значит, что закон распределения величины ξ может быть записан в виде
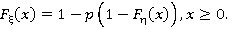 (3.3.)
(3.3.)
При нахождении числовых характеристик 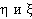 обозначим
обозначим
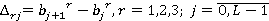 .
.
В результате получаем следующие формулы:
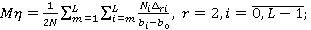 (3.4.)
(3.4.)
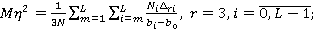 (3.5.)
(3.5.)
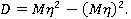 (3.6.)
(3.6.)
Это значит, что математическое ожидание и дисперсия величины ξ могут быть найдены, соответственно, по формулам
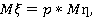 (3.7.)
(3.7.)
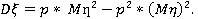 (3.8.)
(3.8.)
Таким образом, для величины иска по одному договору страхования найден явный вид закона распределения и получены формулы для числовых характеристик.
иска по одному договору страхования найден явный вид закона распределения и получены формулы для числовых характеристик.
Литература:
1. Фалин Г. И. Математический анализ рисков в страховании / Г. И. Фалин. — М.: Российский Юридический Издательский Дом, 1994. — 130с.
2. Платонов М. Л. Комбинаторные числа / М. Л. Платонов. — Иркутск, 1980. — 103с.







