Для большинства элементов и приборов на основе МДП-структур одним из важнейших параметров является пороговое напряжение [1].
Точный расчет этого параметра затруднен в связи с неопределенностью значений встроенного заряда в диэлектрике и распределения поверхностных состояний на границе раздела диэлектрик — полупроводник. Поэтому для достижений расчетного значения используют подгонку параметра с помощью ионной имплантации [1]. Но одновременно с пороговым напряжением происходит изменение других параметров и характеристик структуры. Наиболее негативное влияние ионная имплантация оказывает на поверхностную подвижность носителей заряда, которая уменьшается с увеличением дозы. Это ухудшает функциональные возможности элементов. Снижение подвижности в МДП-транзисторе уменьшает крутизну передаточной характеристики, граничную рабочую частоту элемента, ухудшает статические и динамические характеристики. У приборов с зарядовой связью также возрастают потери информационного сигнала.
Снижение дозы ионной имплантации возможно за счет уточненного расчета значения порогового напряжения еще на ранних стадиях проектирования МДП-структуры. Для формирования структуры используют однородно легированную полупроводниковую подложку, поэтому достаточно рассмотреть одномерную модель.
Производители элементной базы под пороговым напряжением понимают значение напряжения на затворе, при котором в МДП-транзисторе возникает так называемый предпороговый ток, не превышающий определенного минимального значения [2]. Более универсальным, особенного на стадии расчета, является значение напряжения затвора, при котором поверхностный потенциал полупроводника соответствует началу сильной инверсии поверхности. При начале инверсии поверхностные концентрации электронов и дырок равны: ps=ns=ni. При начале сильной инверсии поверхностная концентрация неосновных носителей равна значению объемной концентрации основных носителей заряда. Тогда падение напряжения Vsc на приповерхностной области объемного заряда (ПООЗ) полупроводника должно быть равно:
Vsc= (kT/q) ys = (kT/q) 2ln(λ), (1)
где k — постоянная Больцмана; T — температура по шкале Кельвина; q — заряд электрона по модулю; ys — поверхностный безразмерный потенциал, отсчитанный от положения собственного уровня Ферми в нейтральном объеме; λ = p0/ni = ni/n0 — степень (уровень) легирования.
Значение ys, которое определяется равенством (1), задает начало сильной инверсии (yinv).
Теперь рассмотрим выражение для расчета порогового напряжения, которое часто используется в различных методиках и алгоритмах расчета:
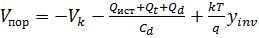, (2)
где Vk — контактная разность потенциалов, равная разности работ выхода электрона из полупроводника и металла; Qист — заряд ПОПЗ; Qt — эффективный заряд поверхностных состояний; Qd — эффективный встроенный заряд диэлектрика.
Для идеальной МДП структуры значения Vk, Qист и Qd равны нулю.
Совершенствование технологии производства позволили уменьшить влияние неконтролируемых зарядов и производить расчет по модели, которая учитывает только контактную разность потенциалов. Заряд Qист рассчитывался в приближении резкого p-n перехода:
,
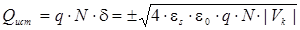и используя равенство (1) окончательно получаем:
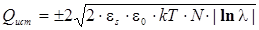, (3)
где N — эффективная концентрация ионизированной примеси в полупроводниковой подложке, определяющая объемную концентрацию основных носителей заряда; ε0 –диэлектрическая постоянная; εs — относительная диэлектрическая проницаемость полупроводника [2–3].
Для более корректного расчета порогового напряжения необходимо решить уравнение Пуассона с учетом заряда подвижных носителей. В результате первого интегрирования имеем следующее равенство:
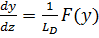, (4)
и для полупроводника в равновесном состоянии: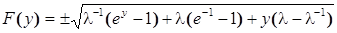 
, (5)
где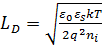 
— длина Дебая собственного полупроводника.
Правило знаков для F(y) следующее: при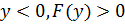 
, и наоборот.
Из уравнения (4) очевидно, что функция F(y) есть напряжённость электрического поля в ПООЗ с точностью до множителя kT/q. Используя теорему Гаусса, получим выражение для расчета поверхностной плотности заряда на границе полупроводник — диэлектрик:
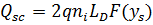. (6)
Для расчета порогового напряжения через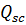 
необходимо задать значение ys в выражениях (5–6) равным 
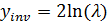и заменить в выражение (2) Qист на .
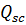Теперь оценим, насколько оправдано предложенное усложнение. Для идеальной структуры Vk, Qd и Qt равны нулю. Тогда:
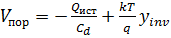. (7)
Для расчета возьмем типовые значения параметров кремниевых интегральных МОП — транзисторов при температуре 300К: толщина окисла 20 нм, λ = 103…105 [1, 4]. Результаты приведены в таблице 1.
Таблица 1
Абсолютная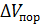 
и относительная 
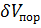погрешности расчета порогового напряжения
|
Параметр легирования λ |
|
|
|
1013 |
76 |
10,75 |
|
1015 |
5,6 |
0,34 |
Для высокоомных подложек погрешность расчета является наиболее существенной.
Если в выражении (2) учитывать все факторы, определяющие пороговое напряжение реальной МДП- структуры, то относительная погрешность расчета может уменьшиться, но абсолютное значение останется прежним. А именно абсолютное значение определяет дозу ионной имплантации области канала для подгонки значения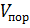 
.
Кроме того, значение абсолютной погрешности соизмеримо со слагаемыми значения напряжения плоских зон, которые определяются величинами Qt, Qd. Это означает, что при экспериментальных исследованиях этих параметров результаты и их интерпретация становятся недостоверными. Поэтому невозможно при испытаниях тестовых образцов установить истинную причину отклонения расчетных значений от экспериментальных. Усложняется и контроль технологических режимов процессов формирования МДП- структур [4]. При чем, в открытых алгоритмах САПР до сих пор используется выражение (2) [5]. Следовательно, при применении САПР для расчета и проектирования МДП — элементов желательно «перепроверить» вычисления порогового напряжения заменяя в выражение (6) Qист на .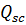
Литература:
1. Рабаи, Жан М., Чандраскан, Ананта, Николич, Боривож. Цифровые интегральные схемы. 2-е издание.: Пер. с англ. — М: ООО «И. Д. Вильямс», 2007. — 912 с.
2. http://www.elek.oglib.ru/bgl/4192/323.html
3. http://dssp.petrsu.ru/book/chapter6/part11.shtml
4. lib.yar.ru/yarcln/edoc/yarsu/pdf/190200.pdf
5. www.rodnik.ru/product/sapr/edaexpress/
