Дается краткий анализ трех моделей симбиоза двух популяций, представленных задачами Коши для обыкновенных дифференциальных уравнений. Математическая модель симбиоза двух популяций на отрезке представлена краевой задачей для системы двух нелинейных уравнений в частных производных. Исследуется устойчивость стационарных состояний. Для построения численного решения нелинейных уравнений используется конечно-разностный метод.
Ключевые слова: популяция, краевые задачи, математическое моделирование.
Введение. Взаимодействие между видами, приносящее обоюдную пользу каждому из них, называется симбиозом. Преимущества, получаемые при таких взаимодействиях, могут быть разными. Это и защита от внешних врагов, и благоприятные условия для размножения, и улучшение трофического ресурса, и многое другое. В литературных источниках приводятся различные варианты благотворительного влияния друг на друга проживающих в биоценозах видов [4, 5, 7, 9, 20, 22, 29, 30, 40, 42–44, 51–53, 61, 62, 64]. В сегодняшнем технологическом укладе в экономике [10] появились новые формы симбиоза у человека. Прежде всего, это симбиоз человек-техника и симбиоз различных социальных групп [2, 12, 14, 18, 32, 35, 38, 39, 45, 46, 48]. Разработка математических моделей для таких систем является более сложной задачей [25, 55, 58, 62], чем для биологических популяций. Несмотря на обилие различных примеров симбиоза, математическому моделированию этого взаимодействия между популяциями посвящено, по сравнению с моделями одиночной популяции и системами «хищник-жертва» и «конкуренция» [3, 6, 8, 11, 13, 19, 23, 26, 27, 56, 60], незначительное число работ [3, 57, 62]. Как правило, в литературных источниках исследуются «модернизированные» модели Вольтерра [3, 6, 62]. Основными задачами в анализе математических моделей являются поиск стационарных положений равновесия, исследование их устойчивости [1, 16, 17, 21, 47, 54, 59], нахождение аналитических решений и разработка алгоритмов построения численных решений обыкновенных дифференциальных уравнений [3, 15, 36, 37, 50] и нелинейных уравнений в частных производных [28, 33, 34. 49].
Точечные математические модели. Модель Вольтера симбиоза двух популяций, представляющая собой задачу Коши для обыкновенных дифференциальных уравнений, имеет вид [3, 62]
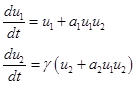 (1)
(1)
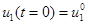 ,
, 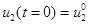 .
.
В этих уравнениях 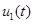 и
и 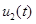 — численности первой и второй популяций;
— численности первой и второй популяций; 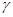 ,
, 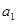 и
и 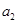 — положительные постоянные;
— положительные постоянные; 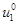 и
и 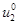 — начальные значения функций
— начальные значения функций 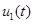 и
и 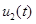 .
.
Решение системы уравнений (1) будет возрастающим при любых положительных значениях 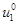 и
и 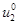 . Эта модель далека от описания реального роста численности популяций, поскольку в отсутствие симбиоза (при
. Эта модель далека от описания реального роста численности популяций, поскольку в отсутствие симбиоза (при 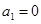 и
и 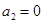 ) численность популяций неограниченно возрастает. В природе численность популяций ограничена сверху по разным причинам и, прежде всего, из-за ограниченности трофического ресурса [4, 8]. При малых численностях рост популяции, как правило, происходит по экспоненциальному закону [3, 4, 31].
) численность популяций неограниченно возрастает. В природе численность популяций ограничена сверху по разным причинам и, прежде всего, из-за ограниченности трофического ресурса [4, 8]. При малых численностях рост популяции, как правило, происходит по экспоненциальному закону [3, 4, 31].
Ограниченность ресурсов и экспоненциальный рост популяции при малой ее численности учитывается в модели [3, 62]
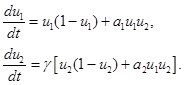 (2)
(2)
В отсутствие взаимодействия между популяциями (при 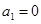 и
и 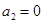 ) эта модель переходит в модели двух не взаимодействующих логистических популяций с единичными емкостями сред обитания [11]. Максимальная численность популяций в стационарном состоянии в этом случае равна единице.
) эта модель переходит в модели двух не взаимодействующих логистических популяций с единичными емкостями сред обитания [11]. Максимальная численность популяций в стационарном состоянии в этом случае равна единице.
Система уравнений (2) может иметь четыре стационарные точки.
1. 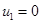 ,
, 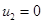 .
.
Матрица Якоби правой части уравнений в (2)
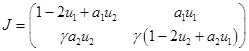
в этой стационарной точке имеет положительные собственные значения 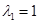 ,
, 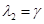 . Поэтому эта стационарная точка будет неустойчивой.
. Поэтому эта стационарная точка будет неустойчивой.
2. 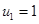 ,
, 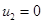 .
.
Поскольку из двух собственных значений 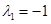 ,
, 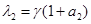 матрицы Якоби правой части уравнений (2) одно положительное, то эта стационарная точка тоже будет неустойчивой.
матрицы Якоби правой части уравнений (2) одно положительное, то эта стационарная точка тоже будет неустойчивой.
3. 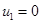 ,
, 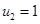 .
.
Эта стационарная точка будет неустойчивой, поскольку матрица Якоби правой части уравнений имеет одно отрицательное и одно положительное собственное значение: 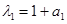 ,
, 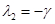 .
.
4. Четвертая стационарная точка
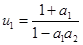 ,
, 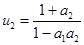 .
.
реализуется, если 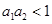 , при этом стационарные значения будут больше единицы. То есть в этой модели симбиоз «увеличивает» стационарные значения
, при этом стационарные значения будут больше единицы. То есть в этой модели симбиоз «увеличивает» стационарные значения 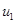 и
и 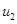 , по сравнению с его отсутствием. В этой стационарной точке характеристический полином матрицы Якоби
, по сравнению с его отсутствием. В этой стационарной точке характеристический полином матрицы Якоби
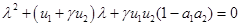
имеет отрицательные корни. Поэтому эта стационарная точка будет устойчивой.
Если выполняется неравенство 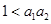 , то функции
, то функции 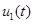 и
и 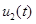 будут возрастающими функциями времени: при больших по сравнению с единицей (при высоком уровне положительного воздействия популяций друг друга) значениих параметров
будут возрастающими функциями времени: при больших по сравнению с единицей (при высоком уровне положительного воздействия популяций друг друга) значениих параметров 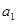 и
и 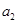 .
.
Скорость роста популяций в моделях симбиоза (1) и (2) пропорциональна произведению 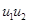 . То есть влияние одной популяции на другую определяется всей ее «численностью». В реальных системах такой вклад в скорость роста численности популяций должен быть ограниченным. Это учитывается в модели [3, 62]
. То есть влияние одной популяции на другую определяется всей ее «численностью». В реальных системах такой вклад в скорость роста численности популяций должен быть ограниченным. Это учитывается в модели [3, 62]
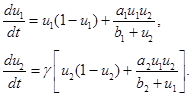 (3)
(3)
Эта система уравнений имеет четыре стационарные точки, три их которых
1) 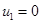 ,
, 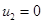 ,
,
2) 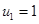 ,
, 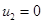 ,
,
3) 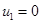 ,
, 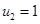
неустойчивые.
Четвертая стационарная точка является единственным решением системы уравнений
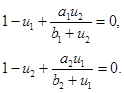
Имеющее физический смысл решение этой системы уравнений удовлетворяет условиям: 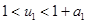 ,
, 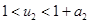 . То есть стационарные значения
. То есть стационарные значения 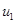 и
и 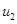 в этой модели симбиоза больше чем, чем в его отсутствие.
в этой модели симбиоза больше чем, чем в его отсутствие.
Характеристический полином матрицы Якоби правой части системы уравнений (3) в этой стационарной точке
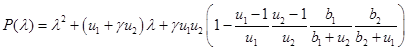
имеет отрицательные корни. Поэтому эта стационарна точка будет устойчивой.
Модели «реакция-диффузия». Популяции существуют на ограниченных территориях, плотность распределения особей по территории не является одинаковой в разных местах их существования. При моделировании взаимодействующих популяций в этом случае используется система уравнений «реакция-диффузия» [11, 27, 62], обоснование которое дается на основе основных гипотез механики сплошных сред [24, 41, 62]. Для случая прямолинейного отрезка 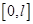 математическая модель двух взаимодействующих популяций представлена начально-краевой задачей для системы двух дифференциальных уравнений в частных производных [27, 62, 63]
математическая модель двух взаимодействующих популяций представлена начально-краевой задачей для системы двух дифференциальных уравнений в частных производных [27, 62, 63]
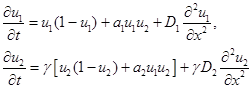 (4)
(4)
для модели (2) и системой уравнений
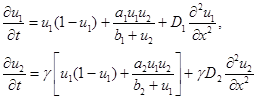 (5)
(5)
для модели (3).
В (4) и (5) 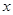 — координата,
— координата, 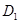 и
и 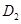 — коэффициенты, характеризующие подвижности особей в популяциях [11].
— коэффициенты, характеризующие подвижности особей в популяциях [11].
К системам уравнений (4) и (5) добавляются начальные условия
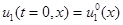 ,
, 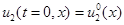 ,
,
задающие значения функций 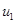 и
и 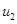 в начальный момент времени.
в начальный момент времени.
В качестве граничных условий будут рассматриваться условие нулевой численности популяций в точке 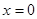 и условие наполнение среды в точке
и условие наполнение среды в точке 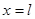 :
:
при 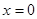 :
: 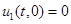 ,
, 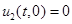 ; (6)
; (6)
при 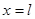 :
: 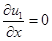 ,
, 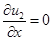 . (7)
. (7)
Поскольку 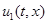 и
и 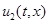 представляют собой линейную плотность особей, то общая численность популяций на отрезке подсчитывается по формулам
представляют собой линейную плотность особей, то общая численность популяций на отрезке подсчитывается по формулам
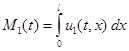 ,
, 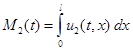 .
.
При граничных условия (6)-(7) как системе уравнений (4), так и системе уравнений (5) в стационарном случае удовлетворяет решение 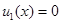 ,
, 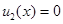 . Пусть наряду с этим решением существует близкое к нему решение
. Пусть наряду с этим решением существует близкое к нему решение 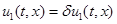
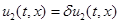 такое, что
такое, что 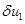 и
и 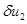 малые положительные величины в каждой точке промежутка
малые положительные величины в каждой точке промежутка 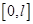 . С учетом этого система уравнений (4) (система уравнений (5)) в линейном приближении примет вид
. С учетом этого система уравнений (4) (система уравнений (5)) в линейном приближении примет вид
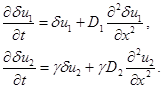
Удовлетворяющие этим уравнениям и граничным условиям (6) и (7) функции 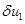 и
и 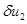 представляются в виде тригонометрических рядов
представляются в виде тригонометрических рядов
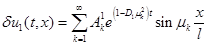 ,
,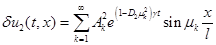 , (8)
, (8)
где 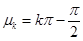 (
(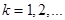 ). Постоянные коэффициенты
). Постоянные коэффициенты 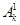 и
и 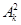 находятся из удовлетворения начальным условиям.
находятся из удовлетворения начальным условиям.
Из (8) следует, что при выполнении неравенства 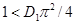 (
(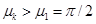 для всех
для всех 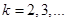 ) функция
) функция 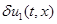 будет убывающей функцией времени, а при выполнении неравенства
будет убывающей функцией времени, а при выполнении неравенства 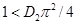 убывающей будет и функция
убывающей будет и функция 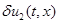 . В этом случае тривиальное решение
. В этом случае тривиальное решение 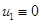 (тривиальное решение
(тривиальное решение 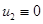 ) будет устойчивым. Этот результат означает, что при высокой подвижности особей малочисленные популяции могут погибнуть [11], а влияние «симбиоза» при малой численности популяций не «ощущается» на росте их численности.
) будет устойчивым. Этот результат означает, что при высокой подвижности особей малочисленные популяции могут погибнуть [11], а влияние «симбиоза» при малой численности популяций не «ощущается» на росте их численности.
Системы уравнений (4) и (5) являются нелинейными, построить их аналитической решение не представляется возможным. Для построения решений используются различные численные методы [11, 28, 37, 49, 50].
Решение системы уравнений (4), удовлетворяющее граничным условиям (6)-(7) в первом приближении представимо в виде
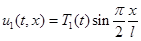 ,
, 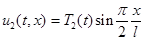 . (9)
. (9)
Тогда из (4) с применением метода Бубнова-Галеркина [28, 36] будет получена система обыкновенных дифференциальных уравнений для нахождения функций 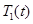 и
и 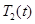
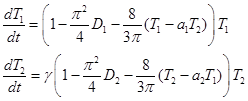
Имеющая физический смысл нетривиальная стационарная точка этой системы уравнений
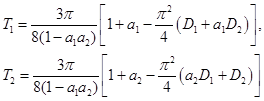
при одновременном выполнении неравенств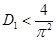 и
и 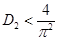 существует, если, как и в случае уравнений (2), выполняется неравенство
существует, если, как и в случае уравнений (2), выполняется неравенство 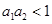 . Как следует из сопоставления значений стационарных точек в точечной модели (2) и модели «реакция-диффузия» (4) стационарные значения численности популяций будут больше, чем при отсутствии симбиоза.
. Как следует из сопоставления значений стационарных точек в точечной модели (2) и модели «реакция-диффузия» (4) стационарные значения численности популяций будут больше, чем при отсутствии симбиоза.
Решение (9) предполагает, что в начальный момент времени плотность популяций изменяется вдоль отрезка по закону синуса. Если же в начальный момент времени «особи» сосредоточены в окрестности отдельной точки, то представление решения в виде одного члена разложения в тригонометрическом ряде будет «грубым» приближением к аналитическому решению. Для построения решения нелинейных уравнений в этом случае используются различные вариационные методы [28, 36, 49], обеспечивающие сходимость к аналитическому решению начально-краевой задачи. Для случая симбиоза более эффективными при построении численного решения являются «сеточные» методы [26, 28, 50], использующие консервативные разностные схемы [28, 47].
Решение уравнений (5) на отрезке длиной 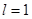 при граничных условиях (6) — (7) и начальном условии
при граничных условиях (6) — (7) и начальном условии
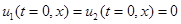 , если
, если 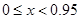 ,
,
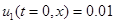 ,
, 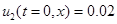 , если
, если 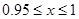
решалось с применением метода сеток [28]. Некоторые из результатов численного моделирования представлены на рис. 1–2 для случая 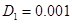 ,
, 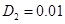 ,
, 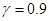 ,
, 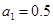 ,
, 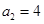 ,
, 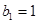 ,
, 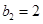 . На рис. 1 приведены расчетные зависимости
. На рис. 1 приведены расчетные зависимости 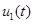 и
и 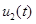 для уравнений (3) (Р — кривые) и зависимости
для уравнений (3) (Р — кривые) и зависимости 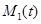 и
и 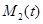 (D — кривые) для уравнений (5). На рис. 2 приведены зависимости функции
(D — кривые) для уравнений (5). На рис. 2 приведены зависимости функции 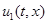 от координаты в моменты времени
от координаты в моменты времени 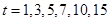 . Как следует из приведенного примера «освоение» территории при рассмотренном начальном «заселении» происходит постепенно из мест с большей численностью особей в места с меньшей численностью (рис. 2). При этом общая численность популяций в модели «реакция-диффузия» может значительно на отдельных временных интервалах отличаться от значений, следуемых их «точечной» модели (рис. 1).
. Как следует из приведенного примера «освоение» территории при рассмотренном начальном «заселении» происходит постепенно из мест с большей численностью особей в места с меньшей численностью (рис. 2). При этом общая численность популяций в модели «реакция-диффузия» может значительно на отдельных временных интервалах отличаться от значений, следуемых их «точечной» модели (рис. 1).
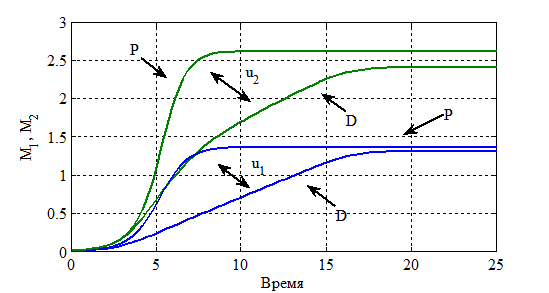
Рис. 3. Зависимость функций 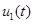 ,
, 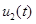 ,
, 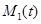 и
и 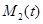 от времени
от времени
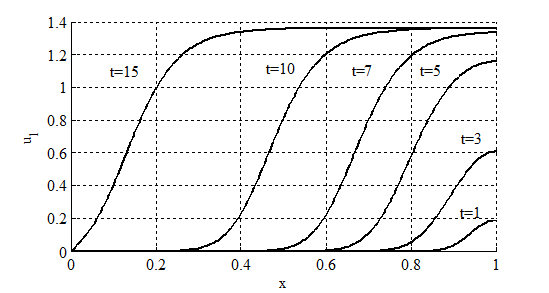
Рис. 2. Зависимость функции 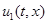 от координаты в различные моменты времени
от координаты в различные моменты времени
Заключение. Как следует из проведенного анализа в математических моделях симбиоза двух популяций с ограниченной емкостью среды общая численность популяций будет больше, чем в случае их «независимого» друг от друга существования. Прогнозы общей численности популяций по «точечной» модели и по модели «реакция-диффузия» могут отличаться значительно. При этом в модели «реакция-диффузия» содержится и вариант возможной гибели популяций при их высоких подвижностях.
Литература:
1. Александров А. Ю. К вопросу об устойчивости по нелинейному приближению // Сибирский математический журнал. — 1997. — Т. 38. — № 6. — С. 1203.
2. Амирханов А. Ю. Духовность общества и власти — антагонизм или симбиоз? // Государственная служба. — 2011. — № 1. — С. 116–117.
3. Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. — 368 с.
4. Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества. Т.1. М.: Мир, 1989. — 667 с.
5. Бухарин О. В., Немцева Н. В., Яценко-Степанова Т. Н. Ассоциативный симбиоз гидробионтов и его значение в определении экологического состояния водоёмов // Поволжский экологический журнал. — 2012. — № 3. — С. 356–360.
6. Вольтерра В. Математическая теория борьбы за существование. Москва-Ижевск:, Институт компьютерных технологий, 2004. — 288 с.
7. Гадимов А. Г. Стартовые дозы азота и симбиоз сои с клубеньковыми бактериями Вестник Московского государственного областного университета. — 2011. — № 3. — С. 8–11.
8. Гасратова Н. А., Столбовая М. В., Неверова Е. Г., Бербер А. С. Математическая модель «ресурс-потребитель» // Молодой ученый. — 2014. — № 10 (69). — С. 5–14.
9. Гиляров А. М. В поисках универсальных закономерностей организации сообществ: прогресс на пути нейтрализма // Журнал общей биологии, — 2010. — Т. 71. № 5. — С. 386–401.
10. Глазьев С. Ю. Новый технологический уклад в современной мировой экономике // Международная экономика. — 2010. — № 5. — С. 5–27.
11. Горбунова Е. А., Колпак Е. П. Математические модели одиночной популяции // Вест. С.-Петерб. ун-та. Сер. 10. — 2012. — Вып. 4. — С. 18–30.
12. Ежова Е. Н. Медиа-рекламная картина мира как артефакт культуры: симбиоз СМИ и рекламы // Культурная жизнь Юга России. — 2010. — № 1 (35). — С. 83а-86.
13. Екимов А. В. К вопросу об ограниченности интегральной воронки в билинейных управляемых системах // Системы управления и информационные технологии. — 2014. — Т. 56. — № 2.1. — С. 138–142.
14. Ерешко Е. В. Симбиоз протекционизма и либеральных таможенно-тарифных мер в российской таможенной политике ХIХ века // Историческая и социально-образовательная мысль. — 2009. — № 2. — 100–105.
15. Жабко А. П., Зараник У. П. О приближении решений экспоненциально устойчивых систем дифференциально-разностных уравнений // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 29–38.
16. Жабко А. П., Медведева И. В. Алгебраический подход к анализу устойчивости дифференциально-разностных систем // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 1. — С. 9–20.
17. Жабко Н. А. Параметрическая идентификация моделей динамики судна при наличии квазигармонических возмущений // Системы управления и информационные технологии. — 2013. — Т. 53. — № 3.1. — С. 197–200.
18. Жих М. И. Древняя Русь и великая степь: «симбиоз» или противостояние? // Вопросы национализма. — 2012. — № 11. — С. 47–65.
19. Жукова И. В., Колпак Е. П. Математическая модель солидной опухоли // Естественные и математические науки в современном мире. — 2013. — № 13. — С. 18–25.
20. Зюганов В. В. Симбиоз особо ценных объектов фауны России: как паразит жемчужница усиливает жизнеспособность хозяина — лосося // Использование и охрана природных ресурсов в России. — 2010. — № 1. — С. 29–34.
21. Калинина Е. А. Общие собственные числа двух матриц // Дальневосточный математический журнал. — 2013. — Т. 13. — № 1. — С. 52–60.
22. Каратыгин И. В., Снигиревская Н. С., Викулин С. В. Симбиоз гриба и цианобактерий в девоне // Микология и фитопатология. — 2010. — Т. 44. — № 1. — С. 31–36.
23. Колесин И. Д., Старков В. Н., Гасратова Н. А. Одиночная популяция под антропогенным давлением // Журнал научных публикаций аспирантов и докторантов. — 2014. — № 6 (96). — С. 226–232.
24. Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
25. Колпак Е. П., Бронникова А. И., Полежаев В. Ю. Математическая модель стачечного движения в России в начале XX века // Молодой учёный. — 2015. — № 3 (83). — С. 4–15.
26. Колпак Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире. — 2014. — № 16. — С. 25–41.
27. Колпак Е. П., Горыня Е. В., Крылова В. А., Полежаев Д. Ю. Математическая модель конкуренции двух популяций на линейном ареале // Молодой ученый. — 2014. — № 12 (71). — С. 12–22.
28. Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О. численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4. — С. 20–30.
29. Колпак Е. П., Кувшинова К. В. Костромская больница губернского земства в конце XIX века // Актуальные проблемы гуманитарных и естественных наук. — 2014. — № 9. — С. 60–63.
30. Колпак Е. П., Скороходова Т. В. Математическая модель роста числа учащихся в средней и высшей школах России // В сборнике: Синергетика в естественных науках. Восьмые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. Ответственный редактор: Лапина Г. П. — 2012. — С. 274–275.
31. Колпак Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.
32. Кубышкин С. А. Симбиоз человека и техники // Вестник Майкопского государственного технологического университета. — 2013. — № 2. — С. 40–44.
33. Мальков В. М., Малькова Ю. В Анализ сингулярности напряжений в нелинейной задаче Фламана для некоторых моделей материала // Прикладная математика и механика. — 2008. — Т. 72. — № 4. — С. 652–660.
34. Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для материала Бартенева-Хазановича // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2005. — № 1–2. — С. 49–55.
35. Мартин Б. Д., Шваб Э. Симбиоз: «сосуществование» в хаосе // Историко-биологические исследования. — 2012. — Т. 4. — № 4. — С. 7–25.
36. Матросов А. В. Сходимость степенных рядов в методе начальных функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 1. — С. 41–51.
37. Матросов А. В. Численно-аналитический расчет балок-стенок на линейно-упругом основании // Вестник государственного университета морского и речного флота им. адмирала С. О. Макарова. — 2011. — № 2. — С. 14a-21.
38. Мирошниченко Ю. П. Симбиоз массовой и элитарной культур, как неизбежный процесс эпохи новых технологий // Актуальные проблемы гуманитарных и естественных наук. — 2014. — № 12–2. — С. 319–322.
39. Павлов Б. С. Семейная политика в регионе: симбиоз экономического и нравственного // Журнал экономической теории. — 2010. — № 3. — С. 58–69.
40. Полиенко А. К., Севостьянова О. А., Орлов А. А. Симбиоз живого и косного вещества в уролитах // Известия Томского политехнического университета. — 2010. — Т. 317. — № 1. — С. 10–15.
41. Пронина Ю. Г Лекции по теории упругости. Общие положения // Учеб. пособие / Ю. Г. Пронина; С.-Петерб. гос. ун-т. СПб. 2004.
42. Раилкин А. И. Распределение диатомовых водорослей на продольно обтекаемых плоских поверхностях // Ботанический журнал. — 1991. — Т. 76. — № 11. — С. 1522.
43. Раилкин А. И. Самосборка сообщества морского микрообрастания // Доклады Академии наук. — 1994. — Т. 337. — № 1. — С. 140.
44. Раилкин А. И., Усов Н. В., Казарьян В. В. Пространственное распределение бентосных организмов на экспериментальных пластинах при разной гидродинамической активности вод // Вестник Санкт-Петербургского университета. Серия 3: Биология. — 2004. — № 4. — С. 31–34.
45. Саватеев А. Д. «Арабская весна»: симбиоз глобализации и исламских традиций // Азия и Африка сегодня. — 2012. — № 2 (655). — С. 7–10.
46. Синченко Г. Ч. Аспирант и научный журнал: апартеид или симбиоз? // Вестник Омского университета. — 2010. — № 3. — С. 227–239.
47. Степенко Н. А. О диссипативности неавтономных систем по нелинейному приближению // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2004. — № 3–4. — С. 160–169.
48. Супренков А. А Эмпорион: греко-варварский симбиоз на крайнем западе эллинского мира // Проблемы истории, филологии, культуры. — 2011. — № 4. — С. 337–358.
49. Тамасян Г. Ш. Градиентные методы в вариационной задаче со свободными концами // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 4. — С. 77–84.
50. Утешев А. Ю., Тамасян Г. Ш К задаче полиномиального интерполирования с кратными узлами // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2010. — № 3. — С. 76–85.
51. Харитонашвили Е. В., Лебедева Г. В., Плюснина Т. Ю., Ризниченко Г. Ю., Алехина Н. Д. Эмпирическая модель регуляции метаболизма нитрата в корнях проростков пшеницы // Физиология растений. — 1997. — Т. 44. — № 4. — С. 568.
52. Штарк О. Ю., Борисов А. Ю., Жуков В. А., Неманкин Т. А., Тихонович И. А. Многокомпонентный симбиоз бобовых с полезными почвенными микро- организмами: генетическое и эволюционное обоснование использования в адаптивном растениеводстве // Экологическая генетика. — 2011. — Т. IX. — № 2. — С. 80–94.
53. Щепановская Е. М. Роль биологических теорий в культурном взаимодействии: миф о борьбе за существование и симбиоз как ведущий фактор эволюции // Ценности и смыслы. — 2011. — № 2. — С. 97–106.
54. Aleksandrov A. Yu., Zhabko A. P. Asymptotic stability of solutions of a class of systems of nonlinear differential equations with delay // Russian Mathematics. — 2012. — Т. 56. — № 5. — С. 1–8.
55. Ford N. J., Lumb P. M., Ekaka-a E. Mathematical modeling of plant species interactions in a harsh climate // Journal of Computational and Applied Mathematics. — 2010. — № 234. — С. 2732–2744.
56. Galileev S. M., Matrosov A. V. Method of initial functions: stable algorithms in the analysis of thick laminated composite structures // Composite Structures. — 1997. — V. 39. — № 3–4. — С. 255–262.
57. Garcia-Algarra J., Galeano J, Pastor J. M., Iriondo J. V., Ramasco J. J. Rethinking the logistic approach for population dynamics of mutualist icinteractions // Journal of Theoretica lBiology. — 2014. — № 363. — С. 332–343.
58. Georgelin E., Loeuille N. Dynamics of coupled mutualistic and antagonistic interactions, and their implications for ecosystem management // Journal of Theoretical Biology. — 2014. — № 346. — С. 67–74.
59. Georgescu P., Zhang H. Lyapunov functionals for two-species mutualisms // Applied Mathematics and Computation. — 2014. — № 226. — С. 754–764.
60. Hernandez M.-J. Disentangling nature, strength and stability issues in the characterization of population interactions // Journal of Theoretical Biology. — 2009. — № 261. — С. 107–119.
61. Kovalenko I. B., Krendeleva T. E., Kukharskikh G. P., Timofeev K. N., Riznichenko G. Yu., Rubin A. B., Ustinin D. M., Grachev N. E., Grachev E. A Cyclic electron transport around photosystem i: an experimental and theoretical study. Biophysics. — 2003. — Т. 48. — № 4. — С. 614–623.
62. Murray D. D. Mathematical biology. N. Y. Springer, 2002. — 551 p.
63. Pronina Y. Analytical solution for the general mechanochemical corrosion of an ideal elastic-plastic thick-walled tube under pressure // International Journal of Solids and Structures. — 2013. — Т. 50. — № 22–23. — С. 3626–3633.
64. Railkin A. I., Dobretsov S. V. Effect of bacterial repellents and narcotising substances on marine macrofouling // Russian Journal of Marine Biology. — 1994. — Т. 20. — С. 16.







