Рассмотрение вопроса построения базовой математической модели понижающего преобразователя и его моделирование в пакете прикладных программ «Matlab Simulink».
1. Введение
Импульсные источники электропитания широко применяются в электронике. Они строятся на основе импульсных преобразователей напряжения. Основные типы импульсных преобразователей напряжения: первый — понижающий (Buck), второй — повышающий (Boost) и третий — инвертирующий (Buck-Boost).
Моделирование импульсных преобразователей позволяет сократить время и снизить затраты на разработку конечного устройства. На сегодняшний день многие ведущие производители ШИМ-контроллеров предлагают бесплатное программное обеспечение(ПО), которое позволяет провести максимально точный анализ реакций электрической схемы под управлением их продукции. Главным недостатком предлагаемого ПО является ограниченные возможности анализа импульсного преобразователя как нелинейного динамического объекта.
Математический анализ позволяет описать широтно-импульсный преобразователь различными дифференциальными уравнениями. Вследствие периодической коммутации силовых ключей (транзисторов, диодов) импульсные преобразователи являются схемами с переменным состоянием. Состояние изменяется при коммутации какого-либо силового ключа, поэтому математический анализ таких схем сводится к решению систем дифференциальных уравнений на различных интервалах времени и «сшиванию» согласно законам коммутации полученных решений на границах интервалов (метод припасовывания). Расчет упрощается при переходе от последовательного решения систем уравнений к усредненной системе дифференциальных уравнений. Импульсный преобразователь состоит из нелинейных динамических объектов, обладающих в зависимости от их структуры и вида обратных связей сложным поведением, включающим в себя неустойчивость, бифуркации, хаос и т. д. Поэтому применение линейных законов управления не в состоянии обеспечить желаемую область устойчивости таких нелинейных систем, как широтно-импульсный преобразователь. Математический анализ позволяет ввести возмущающие воздействия и, решив новую систему уравнений, получить нелинейный закон управления.
Моделирование дифференциальных уравнений осуществляется в различных программных продуктах таких как «Matlab», «MathCAD», «Maple». Лидером в области анализа данных является «Matlab (Matrix Laboratory)», который покрывает все области математики и имеет визуализацию данных «Simulink», построенных на основе различных блоков.
Описанию принципа работы регулятора 1-го типа посвящено много трудов [1, с.23 2, с.13]. В данной работе будет рассмотрено построение базовой математической модели и моделирование в пакете прикладных программ «Matlab Simulink» с целью дальнейшего исследования реакций понижающего преобразователя на возмущающие воздействия.
2. Построение математической модели
Схема регулятора 1-го типа для анализа и последующего построения непрерывной модели понижающего регулятора, представлена на рисунке 1
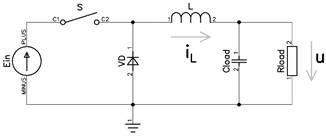
Рис. 1. Схема понижающего регулятора (Buck)
Примем следующие обозначения:
T — период коммутации силового ключа;
fS=1/T — частота коммутации силового ключа;
D1 — относительная длительность проводящего состояния силового ключа;
D2 — относительная длительность от момента размыкания силового ключа S до момента прекращения тока в дросселе L и запирания диода VD1 в режиме прерывистых токов дросселя (DCM). В режиме непрерывных токов дросселя (CCM) она равна (1–D1);
iL — среднее значение тока дросселя L (постоянная составляющая);
u — среднее значение напряжения на нагрузке Rload и Cload или его постоянная составляющая.
При анализе модели пренебрегаем сопротивлениями управляемого ключа S и неуправляемого ключа VD1 в открытом состоянии и падением напряжения на диоде VD1. Строим непрерывную модель регулятора 1-го типа для постоянной частоты коммутации и изменяемого коэффициента заполнения D1 для режима непрерывного (CCM) и прерывистого (DCM) токов дросселя. Рассматриваем широтно-импульсное регулирование проводящего состояния силового ключа.
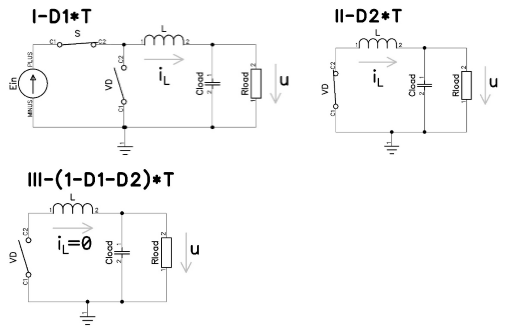
Конфигурация схемы преобразователя в течении периода коммутации с указанием длительности их существования представлены на рисунке 2:
Рис. 2. Конфигурация схемы понижающего преобразователя в течение периода коммутации
Система дифференциальных уравнений в форме Коши для конфигурации «I» составляется по первому и второму законам Кирхгофа:
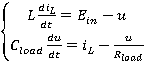 (1.1)
(1.1)
Конфигурация «I» (рисунок 2, «I») существует время D1*T независимости от режима (DCM или ССM) в течение периода коммутации силового ключа S. В течение этого времени ток 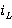 равен току
равен току 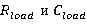 .
.
Система дифференциальных уравнений в форме Коши для конфигурации «II»:
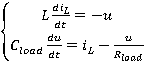 (1.2)
(1.2)
Конфигурация «II» (0, «II») существует время D2*T в режиме непрерывных токов дросселя (CCM) D2=1-D1. В режиме прерывистых токов (DCM) D2 зависит как от параметров схемы, так и от текущих значений переменных состояния (iL, u). В течение этого времени ток 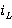 равен току
равен току 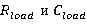 .
.
Определяем относительную длительность интервала D2 следующим способом:
Форма тока в дросселе 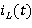 в режиме DCM имеет вид, представленный на рисунке 3.
в режиме DCM имеет вид, представленный на рисунке 3.
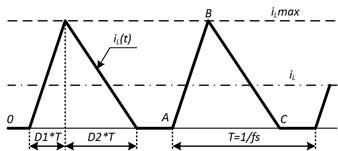
Рис. 3. Ток дросселя в режиме DCM
Среднее значение тока дросселя 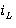 определяется графическим способом:
определяется графическим способом:
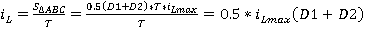 (1.3)
(1.3)
Определяем максимальное значение тока дросселя в прерывистом режиме 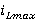 . В течение интервала D1*T, и ток в дросселе нарастает от нуля до
. В течение интервала D1*T, и ток в дросселе нарастает от нуля до 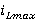 по линейному закону:
по линейному закону:
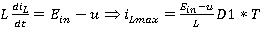 (1.4)
(1.4)
Подставляя уравнение (1.3) в (1.4), выводим конечную формулу для D2:
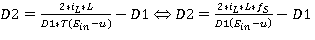 (1.5)
(1.5)
Конфигурация «III» (Рисунок 3, «III») начинается после прекращения тока в дросселе и запирания диода VD1 и существует оставшуюся часть периода (1-D1-D2)*T. В режиме непрерывных токов дросселя конфигурация «III» не начинается или время её существования в течение периода коммутации равно нулю. Система дифференциальных уравнений конфигурации «III» в форме Коши:
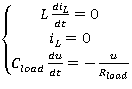 (1.6)
(1.6)
В этом режиме напряжение на выходе поддерживается конденсатором фильтра Cload, ток дросселя равен нулю.
Индуктивность и конденсатор на рисунок 1 представлены идеальными элементами, поэтому дополним схему понижающего преобразователя сопротивлением катушки индуктивности (RL), сопротивлением конденсатора (RC) и управляющим сигналом (u), который принимает значения ноль или единица, рисунок 4:
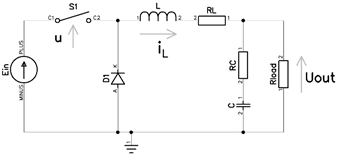
Рис. 4. Схема понижающего преобразователя
Усредненная модель в форме Коши схемы представленной на рисунке4:
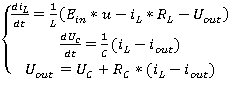 (1.7)
(1.7)
3. Моделирование в «Matlab»
Моделирование системы уравнений (1.7) выполняем в пакете Matlab Simulink, блок схема показана на рисунке 5.
Блок схема ШИМ-сигнала представлена на рисунке 6. Частота коммутации ключа установлена fs=100кГц, соответственно «Time Values» блока «Repeating Sequence» установлен [0 1/fs]. Коэффициент заполнения (dute cycle) задается внешне.
Итоговая блок-схема с идеальным ключом, сопротивлением нагрузки Rload=1Ом, без обратной связи, с фиксированным «dute cycle»=0.5 и входным напряжением Ein=+12В показана на рисунке 7.
Осциллограммы выходного напряжения «Uout» и ток катушки индуктивности «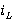 » во время начального переходного процесса понижающего преобразователя, рисунок 8. Проверка реакции системы на изменения коэффициента заполнения, должна показать снижение пульсаций тока индуктивности и повышение выходного напряжения, рисунок 9.
» во время начального переходного процесса понижающего преобразователя, рисунок 8. Проверка реакции системы на изменения коэффициента заполнения, должна показать снижение пульсаций тока индуктивности и повышение выходного напряжения, рисунок 9.
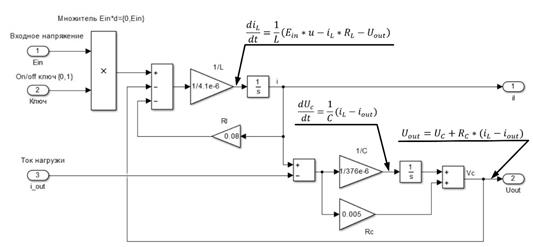
Рис. 5. Усредненная модель понижающего преобразователя в Matlab Simulink
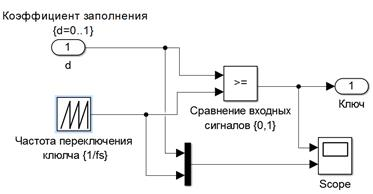
Рис. 6. ШИМ-блок понижающего преобразователя
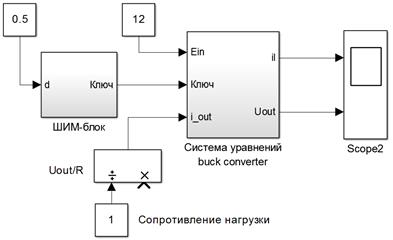
Рис. 7. Блок-схема понижающего преобразователя с идеальным ключом
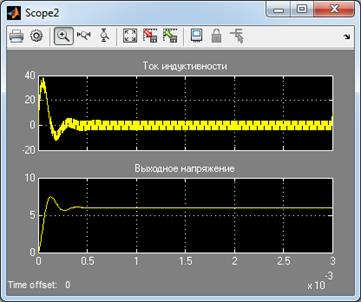
Рис. 8. Осциллограммы «Uout» и «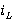 » при d=0.5
» при d=0.5
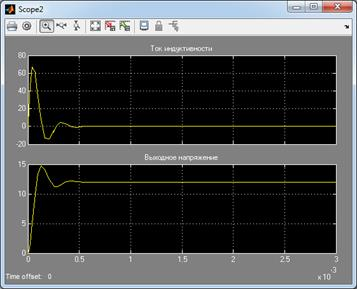
Рис. 9. Осциллограммы «Uout» и «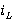 » при d=0.9
» при d=0.9
Изложенное позволяет сделать вывод, что полученная усредненная математическая модель адекватна. Это подтверждают осциллограммы тока индуктивности и выходного напряжения.
Таким образом рассмотрены вопросы построения системы дифференциальных уравнений импульсного понижающего преобразователя и моделирование в «Matlab Simulink». Данная система позволяет производить дальнейшие исследования преобразователя напряжения.
Литература:
1. Marian K. Kazimierczuk «Pulse-width modulated dc–dc power converters», 2008г.
2. R. W. Erickson «Fundamentals of Power Electronics», 1997г.
3. И. В. Черных. «Simulink Инструмент моделирования динамических систем».