Одной из наиболее актуальных и важных задач подготовки детей к школе является развитие логического мышления и познавательных способностей дошкольников, формирование у них элементарных математических представлений, умений и навыков.
При поступлении в школу ребёнок должен уметь устанавливать идентичность предметов и их свойств тому или иному эталону. Однако у большинства детей отсутствует умение анализировать и дифференцировать воспринимаемые предметы. Это говорит о том, что в дошкольных образовательных учреждениях уделяется недостаточное внимание формированию представлений о сенсорных эталонах, в частности об эталонах формы — геометрических фигурах.
В исследованиях современных отечественных и зарубежных психологов и педагогов (В. В. Давыдов, В. В. Данилов, А. А. Столяр, А. М. Пышкало, В. Г. Житомирский, М. Фидлер, В. Лаксон и др.) подчёркивается необходимость обучения детей обобщённым приёмам и способам анализа окружающей действительности по форме.
А. А. Столяр, А. М. Пышкало, В. Г. Житомирский, проблему знакомства детей с геометрическими фигурами и их свойствами рассматривали в двух аспектах: в плане сенсорного восприятия форм геометрических фигур и использования их как эталонов в познании форм окружающих предметов, а также в смысле познания особенностей их структуры, свойств, основных связей и закономерностей в их построении. [1]
Проанализировав точку зрения исследователей, мы пришли к выводу, что представление о форме предмета как границе между предметом и окружающим пространством возникает у детей очень рано. Геометрическая фигура это образец формы предмета, в соответствии с которым подбираются предметы окружающей действительности. По образцу могут выбирать дети и соответствующие геометрические фигуры. Младшие дошкольники свободно выбирают фигуру по данному им образцу, но при условии, если предлагаемые для выбора две фигуры контрастны по форме (квадрат и круг).
Так же необходимо как можно раньше обучать детей правильным приёмам обследования формы геометрической фигуры или предмета по их контурам, а для этого мы предлагаем наиболее эффективное пособие логические блоки, разработанные венгерским психологом и математиком Дьенешем для ранней логической пропедевтики, и, прежде всего для подготовки мышления детей к усвоению математики.
В методической и научно-популярной литературе этот материал можно встретить под разными названиями: «логические фигуры», «логические кубики», «логические блоки», но в каждом из названий подчеркивается направленность на развитие логического мышления. Плоский вариант логических блоков (логические фигуры) используется в современной начальной школе при изучении математики.
Логические блоки лучше изготовить из дерева или пластика. Примерные размеры больших и маленьких фигур (в сантиметрах)
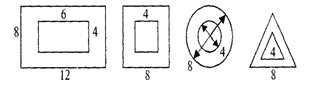
Толстые блоки должны быть толще тонких, по меньшей мере, в два раза.
Наборы плоских логических фигур можно сделать из картона или пластика по примеру логических блоков. Отличительная особенность таких наборов одинаковая толщина всех фигур.
Размеры фигур примерно (в сантиметрах)
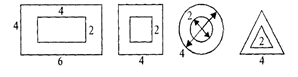
С логическими блоками ребенок выполняет различные действия: выкладывает, меняет местами. Далее убирает, прячет, ищет, делит между «поссорившимися» игрушками и т. д. По ходу выполнения действий ребенок рассуждает.
Игры и упражнения, с блоками проводятся в трёх вариантах.
Первый этап работы посвящается знакомству детей с блоками. Дети учатся выделять, называть, кодировать и декодировать свойства. Полученные знания, закреплять индивидуально, в совместной деятельности и самостоятельно в математическом уголке.
На втором этапе дети учатся группировать блоки по одному из названных свойств.
Третий (заключительный) этап работы отводится упражнениям детей в группировке блоков по двум свойствам [2].
Опишем основные моменты работы, например, воспитатель, сказала детям, что принесла новые кубики, каких у них еще не было. Она поставила четыре столика и высыпала на середину каждого из них разноцветные геометрические фигурки, предварительно рассмотренные по форме: на один стол — круги, на второй — треугольники, на третий — квадраты, на четвертый прямоугольники.
Переходя от стола к столу, детьми проверяли, сравнивали, называли фигуры. Здесь только квадраты, а на том столе лежат треугольники, а там круги и прямоугольники.
Ребенок, видя перед собой какую-либо геометрическую фигуру, перечислял ее признаки: форму, величину, толщину и цвет.
Второе задание направлено на складывание различных предметов из геометрических фигур Дьенеша. Большое познавательное значение имеет создание из блоков домиков, машинок, башен, скворечников и т. п.
В процессе постройки дети убеждаются, что во всем комплекте нет двух совершенно одинаковых геометрических фигур: если, например, геометрическая фигура является голубым толстым кругом, то все другие большие круги или не будут толстые, или толстые, но другого цвета. Если нужен маленький тонкий голубой треугольник, то он будет только один, другого голубого не найдется среди маленьких тонких треугольников [3].
Некоторым детям трудно строить из неодинаковых геометрических фигур Дьенеша, но есть такие дети, что прекрасно справляются с этими заданиями. Например, при постройки автомобиля они получают второе большое толстое красное колесо путем соединения двух тонких колес той же величины, одно из которых красное (оно кладется сверху). Получается, что покрышки этих двух колес одинаково толстые и что оба колеса красные.
Проверить, как дети усвоили свойства геометрических фигур, необходимо познакомить их со знаками кодирования, предложенный материал для дошкольников профессором А. Семадени [4, с.76–83].
Первый ряд — обозначение геометрических фигур; второй ряд — виды толщины (тонкий, толстый); третий ряд — величину (маленький, большой); четвертый ряд — цвет (голубой, желтый, красный.
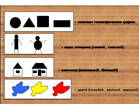
Примеры описания фигур

Схемы, составленные детьми


Описание геометрических фигур с отрицанием
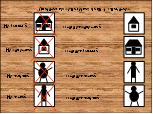
По схеме составить ряд геометрических фигур

Упражнения организуются так, чтобы дети свободно пользовались кодом, знаками отрицания: синий красный желтый

круглый квадратный треугольный прямоугольный
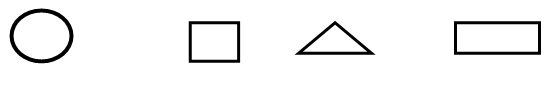
Большой с двумя окнами Маленький с одним окном

Толстый Тонкий

Знаки отрицания
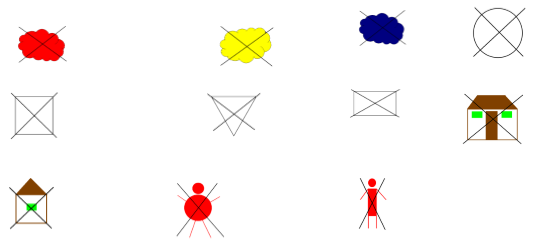
Таким образом, логические блоки Дьенеша дают возможность формировать в комплексе все логические операции мышления, в плане изучения математического содержания, это освоение понятий взаимосвязи изучаемого материала, а также структурные логические связи данного материала с другими темами элементарного предматематического блока.
Литература:
1. Ерофеева Т. И. Использование игровых проблемно-практических ситуаций в обучении дошкольников элементарной математике // Дошкольное воспитание. — 1996.- № 2.
2. Е. Н. Носова, Р. Л. Непомнящая. Логика и математика для дошкольников: Методическое пособие /Авт.-сост. е.Н.Носова, Р. Л. Непомнящая / (Библиотека программы «Детство). — Спб: «Акцидент», 1977. — 79 с.
3. М. Фидлер. Математика уже в детском саду: Пособие для воспитателей дет. сада /Пер. с польск. О. А. Павлович. — М.: Просвещение, 1981. — 159 с.
4. М. Фидлер. Математика уже в детском саду: Пособие для воспитателей дет. сада /Пер. с польск. О. А. Павлович. — М.: Просвещение, 1981. — С. 76–83







